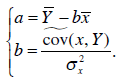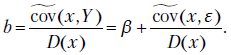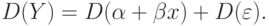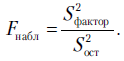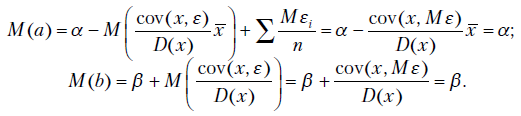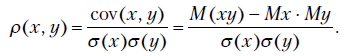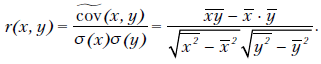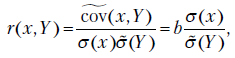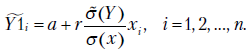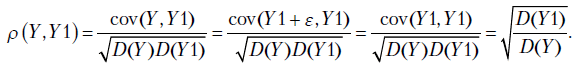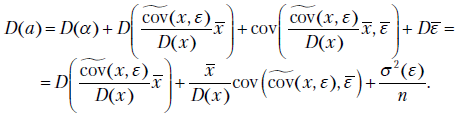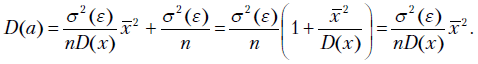|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Парный регрессионный анализ
2.3. Предположения и проверка адекватности уравнения регрессии
Метод наименьших квадратов предполагает ряд ограничений на поведение случайного слагаемого  - условия Гаусса - Маркова:
- условия Гаусса - Маркова:
- нулевое математическое ожидание,
 ;
; - равные дисперсии ошибок для всех наблюдений,
 ;
; - ошибки модели
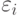 при разных наблюдениях независимы. В частности, корреляционный момент, или ковариация, между
при разных наблюдениях независимы. В частности, корреляционный момент, или ковариация, между 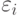 и
и  при
при 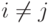 равен
равен  для
для 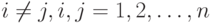 ;
; - для всех
 случайные ошибки
случайные ошибки 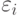 распределены по нормальному закону, а
распределены по нормальному закону, а 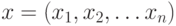 - фиксированный вектор.
- фиксированный вектор.
Одним из показателей качества построенного уравнения регрессии является коэффициент детерминации 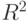 . По определению
. По определению
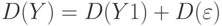 . Действительно,
. Действительно, 
Однако 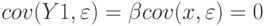 . Что и требовалось. Отсюда
. Что и требовалось. Отсюда
Таким образом, коэффициент детерминации можно интерпретировать как часть общей дисперсии  , которая объяснена с помощью уравнения регрессии, точнее, с помощью расчетной переменной
, которая объяснена с помощью уравнения регрессии, точнее, с помощью расчетной переменной  уравнения регрессии. Максимальное значение коэффициента детерминации
уравнения регрессии. Максимальное значение коэффициента детерминации 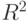 равно
равно  . Это произойдет тогда, когда все остатки
. Это произойдет тогда, когда все остатки  , а уравнение прямой регрессии ляжет точно на экспериментальные точки
, а уравнение прямой регрессии ляжет точно на экспериментальные точки  . Таким образом, при построении регрессии коэффициент детерминации
. Таким образом, при построении регрессии коэффициент детерминации 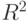 желательно максимизировать. Именно это и делается при применении МНК, так как из формулы (2.7) вытекает, что максимум
желательно максимизировать. Именно это и делается при применении МНК, так как из формулы (2.7) вытекает, что максимум 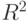 достигается при минимуме
достигается при минимуме  .
.
Проведем дисперсионный анализ уравнения регрессии, построенного выше: . По данным табл. 2.3, используя возможности пакета STATISTICA, получаем следующее (табл. 2.4).
. По данным табл. 2.3, используя возможности пакета STATISTICA, получаем следующее (табл. 2.4).
Таблица 2.4
Итак, 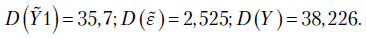 .
.
Отсюда 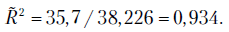
Значение  близко к единице. Это указывает на хорошее (адекватное) описание объясняемой переменной
близко к единице. Это указывает на хорошее (адекватное) описание объясняемой переменной  полученным уравнением регрессии.
полученным уравнением регрессии.
Следует признать, что определить истинные значения коэффициентов  и
и  модели никогда не удастся. Найденные по МНК коэффициенты являются лишь выборочными оценками истинных коэффициентов. Исходя из этого, в отличие от параметров
модели никогда не удастся. Найденные по МНК коэффициенты являются лишь выборочными оценками истинных коэффициентов. Исходя из этого, в отличие от параметров  и
и  , мы их обозначили
, мы их обозначили  и
и  . Выборочные оценки
. Выборочные оценки  и
и  являются случайными величинами, так как зависят от выборки
являются случайными величинами, так как зависят от выборки  и
и  , а также от метода расчета. Поэтому, как это принято в математической статистике, необходимо решить вопрос о несмещенности, эффективности и состоятельности оценок
, а также от метода расчета. Поэтому, как это принято в математической статистике, необходимо решить вопрос о несмещенности, эффективности и состоятельности оценок  и
и  , полученных по МНК. Следует также рассмотреть вопрос о построении доверительных интервалов для
, полученных по МНК. Следует также рассмотреть вопрос о построении доверительных интервалов для  и
и  .
.
Из формул системы уравнений (2.5) теперь следует, что
Поскольку  ,
,


Следовательно,
Итак, выборочный коэффициент регрессии представлен в виде суммы истинного значения  и случайной составляющей, зависящей от
и случайной составляющей, зависящей от  . Аналогично коэффициент
. Аналогично коэффициент  можно разложить на сумму истинного коэффициента
можно разложить на сумму истинного коэффициента  и случайной составляющей
и случайной составляющей
где 
Из формул (2.9) и (2.10) следует: если случайную ошибку  увеличить в
увеличить в  раз, т.е. заменить ошибкой
раз, т.е. заменить ошибкой  , то при определении параметров
, то при определении параметров  и
и  она тоже увеличится в
она тоже увеличится в  раз. Это вытекает из соотношения
раз. Это вытекает из соотношения  .
.
Если нет возможности проверить качество полученного уравнения регрессии на независимой выборке, то проводят оценку значимости уравнения регрессии по  -критерию Фишера. Выдвигается нулевая гипотеза, что коэффициент регрессии
-критерию Фишера. Выдвигается нулевая гипотеза, что коэффициент регрессии  , т.е.
, т.е.  и
и  независимы. Конкурирующая гипотеза:
независимы. Конкурирующая гипотеза:  . Обратимся к равенству
. Обратимся к равенству
В условиях нулевой гипотезы  . Следовательно, нулевая гипотеза эквивалентна гипотезе
. Следовательно, нулевая гипотеза эквивалентна гипотезе  .
.
Рассмотрим линейное уравнение регрессии МНК 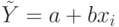 , используя формулы (2.8),
, используя формулы (2.8),
 , или
, или 
Последнее равенство возведем в квадрат и просуммируем по всем наблюдениям 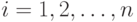 . Получаем
. Получаем
Из формулы (2.12) вытекает, что расчетное значение  является функцией единственного параметра
является функцией единственного параметра  - коэффициента регрессии. Это означает, что сумма квадратов
- коэффициента регрессии. Это означает, что сумма квадратов 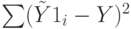 стоящая в числителе
стоящая в числителе 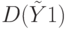 имеет одну степень свободы.
имеет одну степень свободы.
Известно, что число степеней свободы для суммы квадратов, стоящей в числителе дисперсии  независимых наблюдений, равно
независимых наблюдений, равно 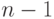 . Согласно теории дисперсионного анализа разложение суммы квадратов на слагаемые влечет соответствующее разложение для степеней свободы слагаемых. Поэтому число степеней свободы суммы квадратов, стоящей в числителе
. Согласно теории дисперсионного анализа разложение суммы квадратов на слагаемые влечет соответствующее разложение для степеней свободы слагаемых. Поэтому число степеней свободы суммы квадратов, стоящей в числителе  , равно
, равно 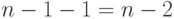 . Далее используем обычную процедуру сравнения дисперсий с различными степенями свободы по
. Далее используем обычную процедуру сравнения дисперсий с различными степенями свободы по  -критерию Фишера, строим исправленные суммы квадратов:
-критерию Фишера, строим исправленные суммы квадратов:
По таблице критических значений Фишера (Приложение 5) находим критическое значение критерия  , где
, где  - выбранный заранее уровень значимости критерия (т.е. вероятность признания регрессии значимой, в то время как она незначима). Если регрессия значима, то
- выбранный заранее уровень значимости критерия (т.е. вероятность признания регрессии значимой, в то время как она незначима). Если регрессия значима, то 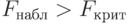 ; в противном случае
; в противном случае  . Уровень значимости
. Уровень значимости  обычно выбирают равным 0,1; 0,05; 0,01; 0,001. При использовании компьютерных расчетов удобнее не выбирать фиксированное значение
обычно выбирают равным 0,1; 0,05; 0,01; 0,001. При использовании компьютерных расчетов удобнее не выбирать фиксированное значение  , а произвести расчет вероятности ошибочного признания регрессии значимой при данном значении
, а произвести расчет вероятности ошибочного признания регрессии значимой при данном значении  . Так, в табл. 2.4 посчитаны значения
. Так, в табл. 2.4 посчитаны значения 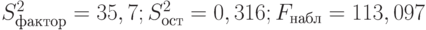 и вероятность того, что регрессия незначима
и вероятность того, что регрессия незначима  . Поэтому вывод о значимости уравнения регрессии можно считать вполне обоснованным.
. Поэтому вывод о значимости уравнения регрессии можно считать вполне обоснованным.
Как известно из курса математической статистики, несмещенность выборочной оценки  параметра генеральной совокупности
параметра генеральной совокупности  означает, что математическое ожидание
означает, что математическое ожидание  равно
равно  . Докажем несмещенность МНК-оценок коэффициентов
. Докажем несмещенность МНК-оценок коэффициентов  и
и  . Необходимо показать, что
. Необходимо показать, что . Исходя из формул (2.9), (2.10), свойств математического ожидания и первого условия Гаусса - Маркова, получаем
. Исходя из формул (2.9), (2.10), свойств математического ожидания и первого условия Гаусса - Маркова, получаем
Что, собственно, и требовалось.
В курсе математической статистики определяется теоретический коэффициент корреляции, являющийся мерой линейной связи между случайными величинами  и
и  ,
,
Аналогично определяется выборочный коэффициент корреляции:
Из формул (2.8) следует, что
а уравнение линейной регрессии можно записать в таком виде:
Покажем, что теоретический коэффициент детерминации равен квадрату теоретического коэффициента корреляции между фактическими  и теоретическими прогнозными значениями
и теоретическими прогнозными значениями 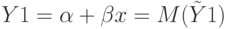 :
:
В целях построения доверительных интервалов для коэффициентов  и
и  воспользуемся формулами расчета дисперсий коэффициентов модели
воспользуемся формулами расчета дисперсий коэффициентов модели  и
и  . Имеем
. Имеем
Но 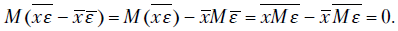 Следовательно,
Следовательно,
Окончательно,
Аналогично получаем, что
Но
Наконец, ранее было доказано, что
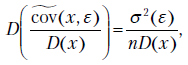 поэтому
поэтому 
Окончательно получаем
Из формул (2.19) и (2.20) можно заключить, что теоретическая дисперсия коэффициентов регрессии зависит от отношения дисперсий случайных ошибок и фактора  . С ростом числа наблюдений
. С ростом числа наблюдений  бесконечности дисперсии коэффициентов стремятся к нулю, что вместе с доказанной выше несмещенностью оценок
бесконечности дисперсии коэффициентов стремятся к нулю, что вместе с доказанной выше несмещенностью оценок  и
и  свидетельствует о состоятельности МНК-коэффициентов регрессии.
свидетельствует о состоятельности МНК-коэффициентов регрессии.
В теории регрессионного анализа также доказывается, что  и
и  в условиях Гаусса - Маркова являются эффективными оценками, т.е. имеют минимальную дисперсию.
в условиях Гаусса - Маркова являются эффективными оценками, т.е. имеют минимальную дисперсию.
На практике теоретическую оценку дисперсии коэффициентов  и
и  получить невозможно, так как неизвестно точное значение дисперсии случайной ошибки
получить невозможно, так как неизвестно точное значение дисперсии случайной ошибки  . Однако, оценив дисперсию остатков, можно получить выборочную дисперсию случайных ошибок.
. Однако, оценив дисперсию остатков, можно получить выборочную дисперсию случайных ошибок.
Как было отмечено, число степеней свободы суммы квадратов, стоящей в числителе  , равно
, равно  . Следовательно, исправленная выборочная дисперсия случайных ошибок равна
. Следовательно, исправленная выборочная дисперсия случайных ошибок равна
Из формул (2.19), (2.20) получаем исправленные выборочные оценки стандартных отклонений (ошибок) МНК-коэффициентов регрессии:
Если бы были известны стандартные отклонения 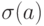 и
и  , то величины
, то величины  и
и  были бы распределены по нормальному закону с нулевым математическим ожиданием и единичной дисперсией:
были бы распределены по нормальному закону с нулевым математическим ожиданием и единичной дисперсией:  . Но поскольку нам известны только выборочные значения стандартных отклонений (стандартные ошибки)
. Но поскольку нам известны только выборочные значения стандартных отклонений (стандартные ошибки) 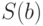 и
и  , соответствующие соотношения
, соответствующие соотношения  и
и  распределены по закону Стьюдента с числом степеней свободы
распределены по закону Стьюдента с числом степеней свободы 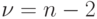 .
.
Заметим, что при  распределение Стьюдента практически не отличается от нормального распределения (Приложение 4). С учетом сказанного можно построить доверительные интервалы для коэффициентов
распределение Стьюдента практически не отличается от нормального распределения (Приложение 4). С учетом сказанного можно построить доверительные интервалы для коэффициентов  и
и  , и если окажется, что в доверительный интервал попадает 0, то соответствующий коэффициент регрессии объявляется незначимым.
, и если окажется, что в доверительный интервал попадает 0, то соответствующий коэффициент регрессии объявляется незначимым.
Незначимые коэффициенты обычно исключают из уравнения регрессии. При расчете уравнения регрессии на компьютере для проверки значимости коэффициентов регрессии вычисляют наблюдаемые значения критерия Стьюдента 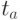 и
и  при
при  и вероятности
и вероятности 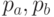 того, что случайная величина, распределенная по критерию Стьюдента, превысит наблюдаемые значения
того, что случайная величина, распределенная по критерию Стьюдента, превысит наблюдаемые значения 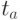 и
и  по абсолютной величине. Если эти вероятности малы (меньше выбранного уровня значимости, например 0,05), то коэффициенты считаются значимыми. В противном случае - незначимыми. Так, построив регрессию
по абсолютной величине. Если эти вероятности малы (меньше выбранного уровня значимости, например 0,05), то коэффициенты считаются значимыми. В противном случае - незначимыми. Так, построив регрессию  по данным табл. 2.1, получаем табл. 2.5.
по данным табл. 2.1, получаем табл. 2.5.
Таблица 2.5
Итак, 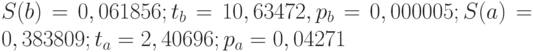 .
.
Из полученных результатов следует значимость коэффициентов  и
и  при уровне значимости 0,05. Как правило, в уравнении регрессии значения стандартных ошибок
при уровне значимости 0,05. Как правило, в уравнении регрессии значения стандартных ошибок  и
и 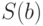 записывают в скобках под соответствующими коэффициентами, иногда под ними указывают значения
записывают в скобках под соответствующими коэффициентами, иногда под ними указывают значения  -критерия. В результате уравнение принимает следующий вид:
-критерия. В результате уравнение принимает следующий вид: