|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Статические и динамические матрицы
Задача 6.10. Решить систему линейных алгебраических уравнений.
При решении этой задачи напишем универсальную функцию решения системы линейных алгебраических уравнений методом Гаусса, а в функции main() просто вызовем эту функцию. Вспомним метод Гаусса.
Пусть дана система линейных алгебраических уравнений (СЛАУ) с  неизвестными
неизвестными
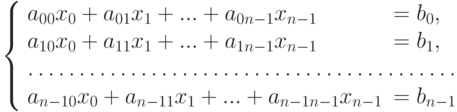 |
( 6.1) |
Обозначим через
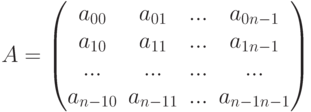
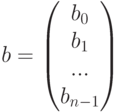 - столбец её свободных членов, и через
- столбец её свободных членов, и через 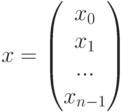 - столбец из неизвестных (искомый вектор). Тогда система (6.1) может быть записана в виде матричного уравнения
- столбец из неизвестных (искомый вектор). Тогда система (6.1) может быть записана в виде матричного уравнения  .
.Наиболее распространённым приёмом решения систем линейных уравнений является алгоритм последовательного исключения неизвестных — метод Гаусса.
При решении систем линейных алгебраических уравнений этим методом всевозможные преобразования производят не над уравнениями системы (6.1), а над так называемой расширенной матрицей системы, которая получается путём добавления к основной матрице  столбца свободных членов
столбца свободных членов  .
.
Первый этап решения системы уравнений, называемый прямым ходом метода Гаусса, заключается в приведении расширенной матрицы (6.2) к треугольному виду. Это означает, что все элементы матрицы (6.2) ниже главной диагонали должны быть равны нулю.
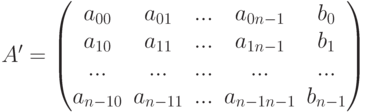 |
( 6.2) |
На первом этапе необходимо обнулить элементы 0-го столбца расширенной матрицы
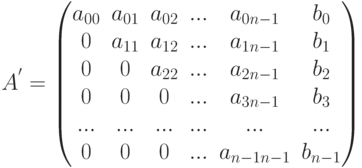 |
( 6.3) |
Для этого необходимо из каждой строки (начиная с первой) вычесть нулевую, умноженную на некоторое число  . В общем виде этот процесс можно записать так:
. В общем виде этот процесс можно записать так:
1-я строка = 1-я строка –  -я строка
-я строка
2-я строка = 2-я строка –  -я строка
-я строка
...
 -я строка =
-я строка =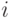 -я строка –
-я строка –  -я строка
-я строка
...
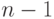 -я строка =
-я строка = 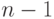 -я строка – M\times 0-я строка
-я строка – M\times 0-я строка
Понятно, что преобразование элементов первой строки будет происходить по формулам:
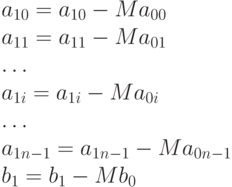
Так как целью данных преобразований является обнуление первого элемента строки, то  выбираем из условия:
выбираем из условия:  . Следовательно,
. Следовательно, 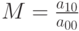 .
.
Элементы второй строки и коэффициент  можно рассчитать аналогично:
можно рассчитать аналогично:
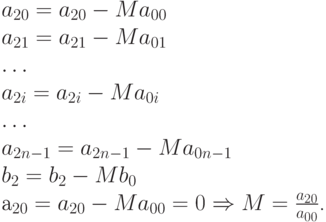
Таким образом, преобразование элементов  –й строки будет происходить следующим образом:
–й строки будет происходить следующим образом:
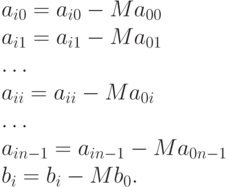
Коэффициент  для
для  –й строки выбирается из условия
–й строки выбирается из условия 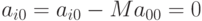 и равен
и равен 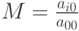 .
.
После проведения подобных преобразований для всех строк матрица (6.2) примет вид
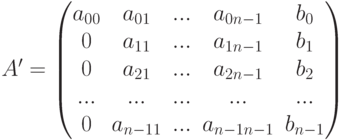
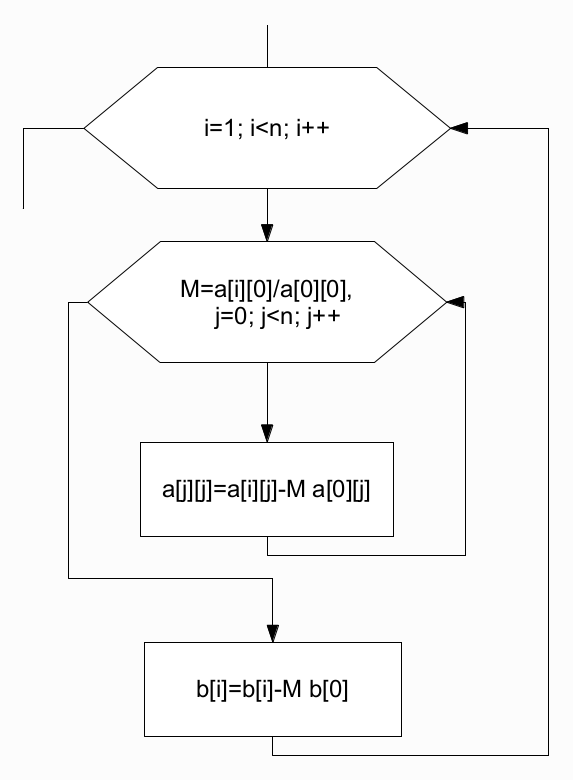
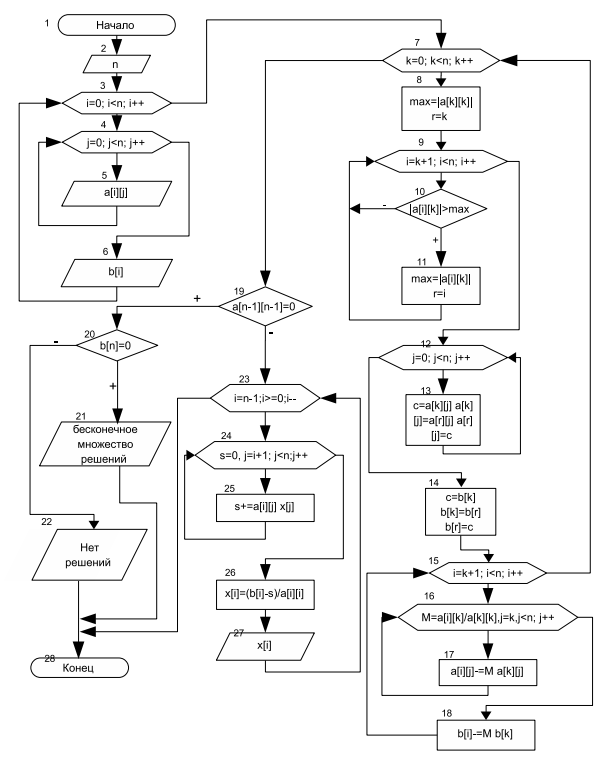
Блок-схема обнуления первого столбца матрицы приведена на рис. 6.10.
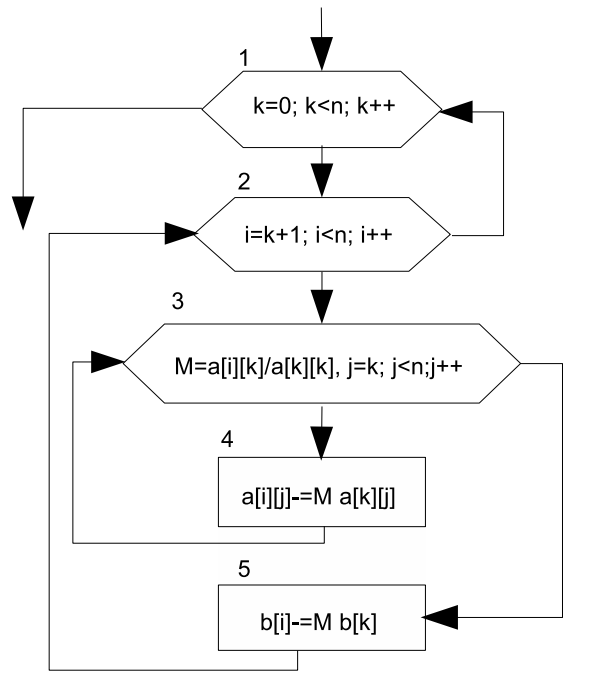
Очевидно, что если повторить описанный выше алгоритм для следующих столбцов матрицы (6.2), то в результате будет получена матрица (6.3). Алгоритм этого процесса изображён на рис. 6.11.
Заметим, что если в матрице (6.2) на главной диагонали встретится элемент 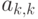 , равный нулю, то расчёт коэффициента
, равный нулю, то расчёт коэффициента  для k
для k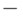 й строки будет невозможен. Избежать деления на ноль можно, избавившись от нулевых элементов на главной диагонали. Для этого перед обнулением элементов в
й строки будет невозможен. Избежать деления на ноль можно, избавившись от нулевых элементов на главной диагонали. Для этого перед обнулением элементов в  –м столбце необходимо найти в нём максимальный по модулю элемент (среди расположенных ниже
–м столбце необходимо найти в нём максимальный по модулю элемент (среди расположенных ниже 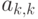 ), запомнить номер строки, в которой он находится, и поменять её местами с
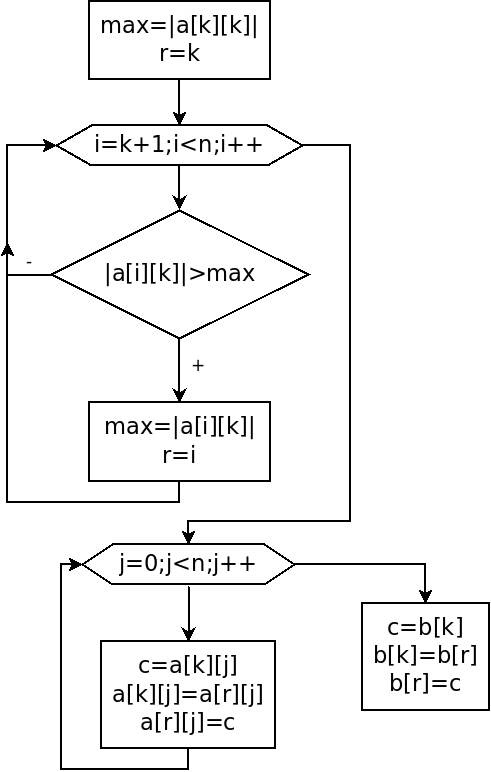
), запомнить номер строки, в которой он находится, и поменять её местами с  -й. Алгоритм, отображающий эти преобразования, приведён на рис. 6.12.
-й. Алгоритм, отображающий эти преобразования, приведён на рис. 6.12.
В результате выполнения прямого хода метода Гаусса матрица (6.2) преобразуется в матрицу (6.3), а система уравнений (6.1) будет иметь следующий вид:
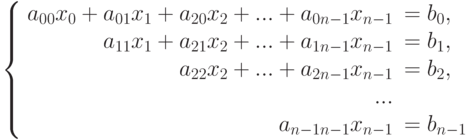 |
( 6.4) |
Решение системы (6.4) называют обратным ходом метода Гаусса.
Последнее 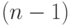 -е уравнение системы (6.4) имеет вид:
-е уравнение системы (6.4) имеет вид: 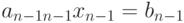 . Тогда, если
. Тогда, если  , то
, то 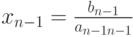 . В случае, если a
. В случае, если a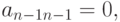 , и
, и 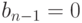 , то система (6.4), а следовательно, и система (6.1) имеют бесконечное множество решений.
, то система (6.4), а следовательно, и система (6.1) имеют бесконечное множество решений.
При  и
и 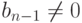 система (6.4), а значит и система (6.1), решения не имеет. Предпоследнее
система (6.4), а значит и система (6.1), решения не имеет. Предпоследнее 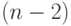 -е уравнение системы (6.4) имеет вид
-е уравнение системы (6.4) имеет вид  .
.
Значит, 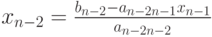 .
.
Следующее 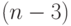 -е уравнение системы (6.4) будет выглядеть так:
-е уравнение системы (6.4) будет выглядеть так:
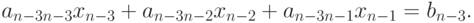
Отсюда имеем
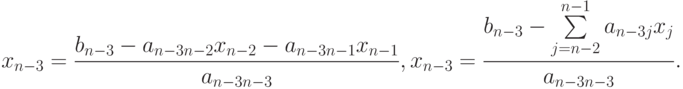
Таким образом, формула для вычисления  -го значения
-го значения  будет иметь вид:
будет иметь вид: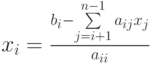 .
.
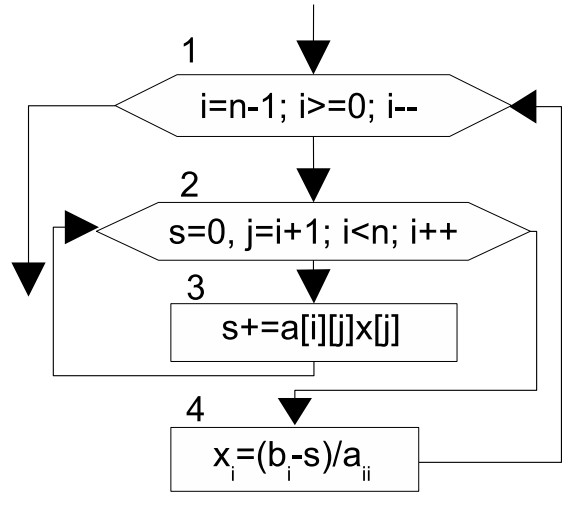
Алгоритм, реализующий обратный ход метода Гаусса, представлен в виде блок-схемы на рис. 6.13.
Объединив блок-схемы, изображённые на рис. 6.11,рис. 6.12 и рис. 6.13, получим общую блок-схему метода Гаусса (рис. 6.14). Блоки 2-6 содержат последовательный ввод данных, где  — это размерность системы линейных алгебраических уравнений, а сама система задаётся в виде матрицы коэффициентов при неизвестных
— это размерность системы линейных алгебраических уравнений, а сама система задаётся в виде матрицы коэффициентов при неизвестных  и вектора свободных коэффициентов
и вектора свободных коэффициентов  . Блоки 7-18 предусматривают прямой ход метода Гаусса, а блоки 23-27 — обратный. Для вывода результатов предусмотрено несколько блоков вывода. Если результат проверки условий 19 и 20 положительный, то выдаётся сообщение о том, что система имеет бесконечное множество решений (блок 21). Если условие 19 выполняется, а 20 — нет, то появляется сообщение о том, что система не имеет решений (блок 22). Сами же решения системы уравнений, представленные вектором
. Блоки 7-18 предусматривают прямой ход метода Гаусса, а блоки 23-27 — обратный. Для вывода результатов предусмотрено несколько блоков вывода. Если результат проверки условий 19 и 20 положительный, то выдаётся сообщение о том, что система имеет бесконечное множество решений (блок 21). Если условие 19 выполняется, а 20 — нет, то появляется сообщение о том, что система не имеет решений (блок 22). Сами же решения системы уравнений, представленные вектором  , вычисляются (блоки 23–26) и выводятся экран/печать (блок 27) только в случае невыполнения условия.
, вычисляются (блоки 23–26) и выводятся экран/печать (блок 27) только в случае невыполнения условия.
Теперь алгоритм решения СЛАУ, представленный на рис. 6.14, разобьём на главную функцию main() и функцию решения СЛАУ методом Гаусса. В функции main() будет находиться ввод исходных данных, обращение к функции SLAU и вывод вектора решения. Функция SLAU предназначена для решения системы линейных алгебраических уравнений методом Гаусса.
При написании функции следует учитывать следующее: в методе Гаусса изменяются матрица коэффициентов и вектор правых частей. Поэтому, для того чтобы их не испортить, в функции SLAU матрицу коэффициентов и вектор правых частей необходимо скопировать во внутренние переменные, и в функции обрабатывать внутренние переменные-копии.
Функция SLAU возвращает значение 0, если решение найдено, -1 — если система имеет бесконечное множество решений, -2 — если система не имеет решений.
Ниже приведено решение задачи 6.10 с подробными комментариями.
#include <iostream>
#include <math.h>
using namespace std;
int SLAU( double ** matrica_a, int n, double *massiv_b, double *x )
//Функция SLAU возвращает значение типа int: 0, если решение найдено, _1 — если система имеет
//бесконечное множество решений, _2 — если система не имеет решений.
//Формальные параметры функции: n — размерность системы,
//matrica_a — матрица коэффициентов СЛАУ,
//massiv_b — вектор правых частей, x — решение СЛАУ, передаются как указатели.
{
int i, j, k, r;
double c,M, max, s;
//Матрица a — копия матрицы коэффициентов, массив b — копия вектора правых частей.
double **a, *b;
a=new double * [ n ]; //Выделение памяти для a и b.
for ( i =0; i<n; i++)
a [ i ]=new double [ n ];
b=new double [ n ];
//В a записываем копию матрицы коэффициентов, в b копию вектора правых частей.
for ( i =0; i<n; i++)
for ( j =0; j<n; j++)
a [ i ] [ j ]=matrica_a [ i ] [ j ];
for ( i =0; i<n; i++)
b [ i ]=massiv_b [ i ];
//Прямой ход метода Гаусса: приводим матрицу a (копию матрицы коэффициентов СЛАУ)
//к диагональному виду.
for ( k=0;k<n; k++)
{ //Поиск максимального по модулю элемента в k-м столбце.
max=fabs ( a [ k ] [ k ] );
r=k;
for ( i=k+1; i<n; i++)
if ( fabs ( a [ i ] [ k ] )>max)
{
max=fabs ( a [ i ] [ k ] );
r= i;
}
for ( j =0; j<n; j++) //Меняем местами k-ю и r-ю (строку, где находится
{ //максимальный по модулю элемент) строки.
c=a [ k ] [ j ];
a [ k ] [ j ]=a [ r ] [ j ];
a [ r ] [ j ]= c;
}
c=b [ k ];
b [ k ]=b [ r ];
b [ r ]= c;
for ( i=k+1; i<n; i++) //Приведение матрицы к диагональному виду.
{
for (M=a [ i ] [ k ] / a [ k ] [ k ], j=k; j<n; j++)
a [ i ] [ j ]-=M*a [ k ] [ j ];
b [ i ]-=M*b [ k ];
}
}
//Обратный ход метода Гаусса.
if ( a [ n-1 ] [ n-1]==0) //Если последний диагональный элемент равен 0 и
if ( b [ n-1]==0) //последний коэффициент вектора свободных членов равен 0,
return -1; //то система имеет бесконечное множество решений
else return -2; //последний коэффициент вектора свободных членов не равен 0,
//система решений не имеет.
else //Последний диагональный элемент не равен 0, начинается обратный ход метода Гаусса.
{
for ( i=n-1; i >=0; i --)
{
for ( s =0, j= i +1; j<n; j++)
s+=a [ i ] [ j ] * x [ j ];
x [ i ]=( b [ i ]- s ) / a [ i ] [ i ];
}
return 0;
}
}
int main ( )
{
int result, i, j,N;
double **a, *b, *x;
cout<<" N = "; //Ввод размерности системы.
cin>>N;
a=new double * [N ]; //Выделение памяти для матрицы правых частей и вектора свободных
членов.
for ( i =0; i<N; i++)
a [ i ]=new double [N ];
b=new double [N ];
x=new double [N ];
cout<<"Ввод матрицы A "<<endl; //Ввод матрицы правых частей
for ( i =0; i<N; i++)
for ( j =0; j<N; j++)
cin>>a [ i ] [ j ];
cout<<"Ввод вектора B "<<endl; //и вектора свободных членов.
for ( i =0; i<N; i++)
cin>>b [ i ];
//Вызов функции решения СЛАУ методом Гаусса. По значению result можно судить, сколько
//корней имеет система. Если result=0, то система имеет единственное решение, result= -1 -
//система имеет бесконечное множество решений, result=-2 — система не имеет решений.
result=SLAU( a,N, b, x );
if ( result ==0)
{ //Вывод массива решения.
cout<<" MassivX "<<endl;
for ( i =0; i<N; i++)
cout<<x [ i ]<<" \t ";
cout<<endl;
}
else if ( result ==-1)
cout<<"Бесконечное множество решений\n ";
else if ( result ==-2)
cout<<"Нет решений\n ";
}