|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Общие сведения о библиотеке MathGL
При решении различных задач возникает необходимость графического отображения данных (графики, диаграммы, поверхности). Одним из универсальных способов построения различных графиков является кросс-платформенная библиотека MathGL.
Mathgl — свободная кросс-платформенная библиотека для построения двух- и трёх-мерных графиков функций. Её использование позволит построить график с помощью нескольких операторов. Синтаксис функций, используемых в MathGL, подобен синтаксису MathLab, Octave, Scilab, GnuPlot. Официальный сайт — http://mathgl.sourceforge.net/doc_ru/Website.html#Website, на странице загрузки http://mathgl.sourceforge.net/doc_ru/Download.html# Download можно скачать последнюю версию программы для различных операционных систем, англоязычную документацию в формате pdf. Группа в Google — https://groups.google.com/forum/#!forum/mathgl. Русскоязычная страница с описанием — http://mathgl.sourceforge.net/doc_ru/index. html#SEC_Contents , англоязычная — http://mathgl.sourceforge.net/doc_en/ index.html#SEC_Contents. Кроме С(С++) поддерживаются Fortran, Python, Octave, скриптовый язык MGL.
Рассмотрим особенности установки и примеры использования библиотеки для построения графиков.
B.1 Установка MathGL в Linux.
Библиотека входит в репозитории большинства современных дистрибутивов Linux. Её можно установить из репозитория стандартным для вашего дистрибутива способом, однако в репозитории зачастую находится не самая новая версия. Для установки самой новой версии необходимо:
- Скачать исходники последней версии с официального сайта.
- Распаковать.
- Последовательно выполнить команды1Перед выполнением команды cmake, возможно, придётся доставлять необходимые пакеты. При работе в debian (6, 7), ubuntu (12.04, 12.10, 13.04, 13.10) авторам пришлось доставить пакеты cmake, zlib1g-dev, libpng12-dev, libqt4-opengl-dev, libqtwebkit-dev. Кроме того, должен быть устанвлен компилятор g++.
cmake -Denable-qt=ON cmake make sudo make install
- Скопировать файлы libmgl-qt.so.7.1.0 и libmgl.so.7.1.02Версии библиотек libmgl указаны применительно к mathgl 2.2, в вашем конкретном случае могут быть другие библиотеки. из каталога /usr/local/lib в каталог /lib (нужны права администратора(суперпользователя)).
После этого для компиляции программы с использованием библиотеки MathGL необходимо использовать ключи -L/usr/local/lib -L/usr/lib -lmgl -lmgl-qt, например для компиляции файла с именем 1.cpp можно использовать команду
g++ -o 1 1.cpp -L/usr/local/lib -L/usr/lib -lmgl -lmgl-qt
B.2 Использование MathGL при построении двух- и трёхмерных графиков
Рассмотрим возможности библиотеки на конкретных примерах.
Задача B.1. Построить график функции f .
.
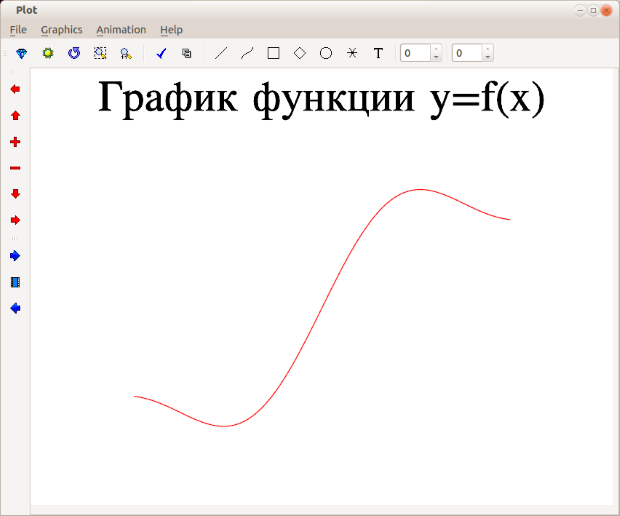
Следующий программный код позволит построить линию графика (рис. B.1) на интервале [-1;1].
#include <mgl2 / qt .h>
int sample ( mglGraph * gr )
{
gr->Title ( "График функции y = f ( x ) " ); //Заголовок графика
//График заданной функции. Линия графика изображена красным цветом — " r " .
gr->Fplot ( " sin ( x ) + 1 / 3 * sin ( 3 * x ) + 1 / 5 * sin ( 5 * x ) ", " r " );
return 0;
}
int main ( int arg c, char ** argv )
{
set locale (LC_CTYPE, " ru_RU.utf8 " );
mglQT gr ( sample, " Plot " );
return gr.Run ( );
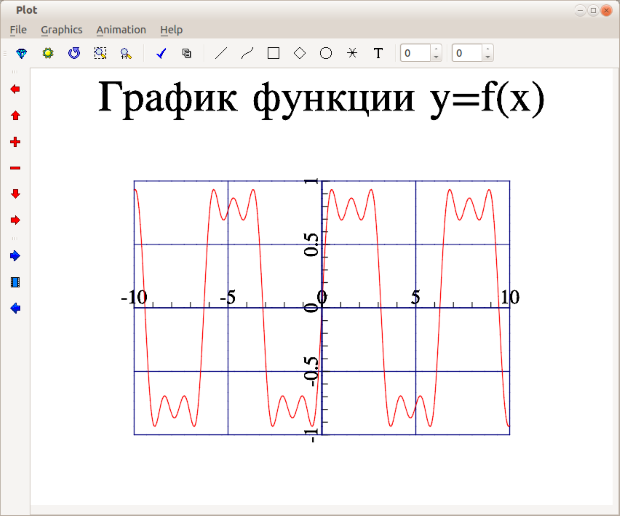
}Далее представлен текст программы, с помощью которого можно усовершенствовать график, показанный на рис. B.1. На рис. B.2 видно, что был увеличен диапазон построения графика, добавлены оси координат, подписи под ними и линии сетки.
#include <mgl2 / qt .h>
int sample ( mglGraph * gr )
{
gr->Title ( "График функции y = f ( x ) " ); //Заголовок графика
gr->setOrigin ( 0, 0 ); //Установка центра координатных осей
//Границы по оси абсцисс от -10 до 10, по оси ординат от -1 до 1.
gr->SetRanges ( -10,10, -1,1);
gr->Axis ( ); //Вывод значений возле осей
gr->Grid ( ); //Линии сетки
//График заданной функции.
gr->Fplot ( " sin ( x ) + 1 / 3 * sin ( 3 * x ) + 1 / 5 * sin ( 5 * x ) ", " r " );
return 0;
}
int main ( int arg c, char ** argv )
{
set locale (LC_CTYPE, " ru_RU.utf8 " ); //Поддержка кириллицы в С++
mglQT gr ( sample, " Plot " ); //Вывод графика на экран в окно с именем Plot
return gr.Run ( );
}Задача B.2. Построить графики функций  и
и 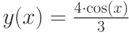 в одной графической области.
в одной графической области.
Далее приведён текст программы, реализующий решение поставленной задачи. Результаты работы программы показаны на рис. B.3.
#include <mgl2 / qt .h>
#include <math.h>
int sample ( mglGraph _ gr )
{
gr->Title ( "Графики функции y = f ( x ) " ); //Заголовок графика
gr->SetRanges ( -15,15, -2,2); //Границы по осям
gr->Axis ( ); //Вывод значений возле осей
gr->Grid ( ); //Линии сетки
gr->Fplot ( " sin ( 2 * x ) ", " r " ); //График функции f(x), красная (r) сплошная линия.
gr->AddLegend ( " sin ( 2 * x ) ", " r " ); //Добавление легенды
gr->Fplot ( " 4* cos ( x ) /3 ", " k." ); //График функции y(x), чёрная (k) линия и точки (.).
gr->AddLegend ( " 4* cos ( x ) /3 ", " k." ); //Добавление легенды
gr->Legend ( 3 ); //Вывод легенды на экран в правом верхнем углу
gr->Label ( " x ", " OX ", 0 ); //Вывод подписи по оси абсцисс
gr->Label ( " y ", " OY " ); //Вывод подписи по оси ординат
return 0;
}
int main ( int arg c, char ** argv )
{
set locale (LC_CTYPE, " ru_RU.utf 8 " );
mglQT gr ( sample, " Plot " );
return gr.Run ( );
}Задача B.3. Построить в одном графическом окне графики функций:
-
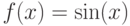 на интервале [-10;10],
на интервале [-10;10], -
 на интервале [-6;6],
на интервале [-6;6], -
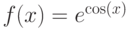 на интервале [-6;6],
на интервале [-6;6], -
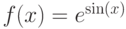 на интервале [-12;12].
на интервале [-12;12].
Результаты вывести на экран и в файл.
Далее приведён программный код и результат его работы (рис. B.4).
#include <mgl2/qt .h>
#include <mgl2/mgl .h>
#include <iostream>
using namespace std;
int sample ( mglGraph * gr )
{
//График функции sin(x) на интервале [-10; 10]
gr->Subplot ( 2, 2, 0 );
gr->Title ( "График функции sin ( x ) " );
gr->setOrigin ( 0, 0 );
gr->SetRanges ( -10,10, -1,1);
gr->Axis ( );
gr->Grid ( );
gr->Fplot ( " sin ( x ) ", " k -. " );
//График функции cos(x) на интервале [-6; 6]
gr->Subplot ( 2, 2, 1 );
gr->Title ( "График функции cos ( x ) " );
gr->setOrigin ( 0, 0 );
gr->SetRanges ( -6,6, -1,1);
gr->Axis ( );
gr->Grid ( );
gr->Fplot ( " cos ( x ) ", " k." );
//График функции exp(cos(x)) на интервале [-6; 6]
gr->Subplot ( 2, 2, 2 );
gr->Title ( "График функции e ^{ cos ( x ) } " );
gr->setOrigin ( 0, 0 );
gr->SetRanges ( -6, 6, 0, 3 );
gr->Axis ( );
gr->Grid ( );
gr->Fplot ( " exp ( cos ( x ) ) ", " r o " );
//График функции exp(sin(x)) на интервале [12; 12]
gr->Subplot ( 2, 2, 3 );
gr->Title ( "График функции e ^{ sin ( x ) } " );
gr->setOrigin ( 0, 0 );
gr->SetRanges ( -15, 15, 0, 3 );
gr->Axis ( );
gr->Grid ( );
gr->Fplot ( " exp ( sin ( x ) ) ", " r - o " );
return 0;
}
int main ( int arg c, char __ argv )
{
//Вывод на экран или в файл
int k;
cout<<"Введите 1, если будете выводить на экран, 2 - если в файл\nk = ";
cin>>k;
if ( k==1)
{
//Поддержка кириллицы в С++
set locale (LC_CTYPE, " ru_RU.utf 8 " );
//Вывод на экран
mglQT gr ( sample, " Plot s " );
return gr.Run ( );
}
else
{
mglGraph gr;
gr.Alpha ( true );
gr.Light ( true );
set locale (LC_CTYPE, " ru_RU.utf 8 " );
//Обращение к функции вывода
sample(& gr );
//Запись изображения в файл
gr.WriteEPS ( " test.eps " );
return 0;
}
}Задача B.4. Построить график функций 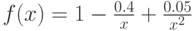 .
.
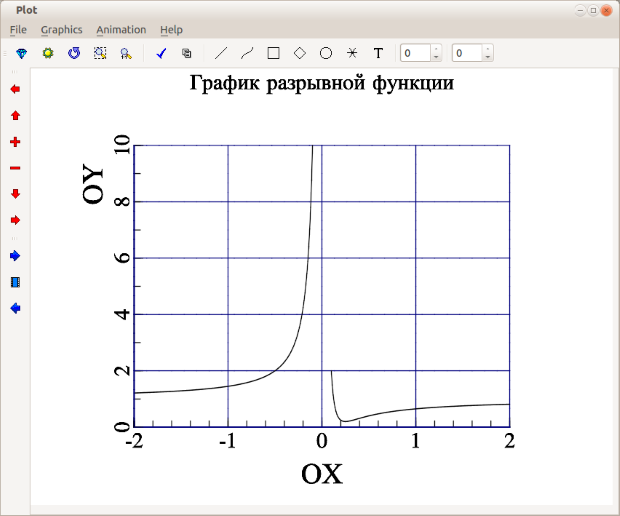
Нетрудно заметить, что функция  не существует в точке ноль. Поэтому построим её график на двух интервалах [-2;-0.1] и [0.1;2], исключив точку разрыва из диапазона построения. Текст программы с подробными комментариями приведён далее. Решение задачи представлено на рис. B.5.
не существует в точке ноль. Поэтому построим её график на двух интервалах [-2;-0.1] и [0.1;2], исключив точку разрыва из диапазона построения. Текст программы с подробными комментариями приведён далее. Решение задачи представлено на рис. B.5.
#include <mgl2 / qt .h>
#include <iostream>
using namespace std;
int sample ( mglGraph * gr )
{
mglData x1 ( 191 ), x2 ( 191 ), y1 ( 191 ), y2 ( 191 );
int i; float h, a1, b1, a2, b2;
//График точечной разрывной функции
//Первый интервал
a1=-2;b1=-0.1;
h = 0.01;
for ( i =0; i <191; i++)
{
x1 [ i ]= a1+ i *h;
y1 [ i ]=1 -0.4/ x1 [ i ]+ 0.05 / x1 [ i ] / x1 [ i ];
}
//Второй интервал
a2 = 0.1; b2=2;
h = 0.01;
for ( i =0; i <191; i++)
{
x2 [ i ]= a2+ i *h;
y2 [ i ]=1 -0.4/ x2 [ i ]+ 0.05 / ( x2 [ i ] * x2 [ i ] );
}
gr->SetRanges ( a1, b2, 0, 10 ); //Границы по оси абсцисс и ординат
gr->Axis ( ); //Оси координат
gr->Grid ( ); //Сетка
gr->Plot ( x1, y1, " k " ); //График функции на первом интервале, чёрный (k) цвет.
gr->Plot ( x2, y2, " k " ); //График функции на втором интервале, чёрный (k) цвет.
gr->set font size ( 2 ); //Размер шрифта
gr->Title ( "График разрывной функции" ); //Заголовок
gr->set font size ( 4 ); //Размер шрифта
gr->Label ( " x ", " OX ", 0 ); //Подпись по оси абсцисс
gr->Label ( " y ", " OY " ); //Подпись по оси ординат
return 0;
}
int main ( int arg c, char ** argv )
{
set locale (LC_CTYPE, " ru_RU.utf 8 " );
mglQT gr ( sample, " Plot " );
return gr.Run ( );
}Задача B.5. Построить график функции 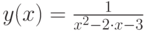 на интервале [-5;5].
на интервале [-5;5].
Функция 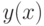 имеет разрыв в точках -1 и 3. Построим её график на трёх интервалах [-5; -1.1], [-0.9;2.9] и [3.1;5], исключив точки разрыва из диапазона построения. Текст программы с подробными комментариями приведён далее. Решение задачи представлено на рис. B.6.
имеет разрыв в точках -1 и 3. Построим её график на трёх интервалах [-5; -1.1], [-0.9;2.9] и [3.1;5], исключив точки разрыва из диапазона построения. Текст программы с подробными комментариями приведён далее. Решение задачи представлено на рис. B.6.
#include <mgl2 / qt .h>
#include <iostream>
using namespace std;
int sample ( mglGraph * gr )
{
mglData x1 ( 391 ), x2 ( 381 ), x3 ( 191 ), y1 ( 391 ), y2 ( 381 ), y3 ( 191 );
int i; float h, a1, b1, a2, b2, a3, b3;
//График точечной разрывной функции
a1=-5;b1=-1.1; //Первый интервал
h = 0.01;
for ( i =0; i <391; i++)
{
x1 [ i ]= a1+ i _h;
y1 [ i ]=1/( x1 [ i ] * x1 [ i ]-2*x1 [ i ] -3);
}
a2=-0.9;b2 = 2.9; //Второй интервал
h = 0.01;
for ( i =0; i <381; i++)
{
x2 [ i ]= a2+ i *h;
y2 [ i ]=1/( x2 [ i ] *x2 [ i ]-2*x2 [ i ] -3);
}
a3 = 3.1; b3=5; //Третий интервал
h = 0.01;
for ( i =0; i <191; i++)
{
x3 [ i ]= a3+ i *h;
y3 [ i ]=1/( x3 [ i ] * x3 [ i ]-2*x3 [ i ] -3);
}
gr->SetRanges ( -6,6, -3,3); //Границы по оси абсцисс и ординат
gr->Axis ( ); //Оси координат
gr->Grid ( ); //Сетка
gr->Plot ( x1, y1, " k " ); //График функции на первом интервале, чёрный (k) цвет.
gr->Plot ( x2, y2, " k " ); //График функции на втором интервале, чёрный (k) цвет.
gr->Plot ( x3, y3, " k " ); //График функции на третьем интервале, чёрный (k) цвет.
gr->set font size ( 2 ); //Размер шрифта
gr->Title ( "График функции c двумя разрывами" ); //Заголовок
gr->set font size ( 4 ); //Размер шрифта
gr->Label ( " x ", " OX ", 0 ); //Подпись по оси абсцисс
gr->Label ( " y ", " OY " ); //Подпись по оси ординат
return 0;
}
int main ( int arg c, char ** argv )
{
set locale (LC_CTYPE, " ru_RU.utf 8 " );
mglQT gr ( sample, " Plot " );
return gr.Run ( );
}Задача B.6. Построить график функции 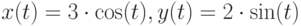 .
.
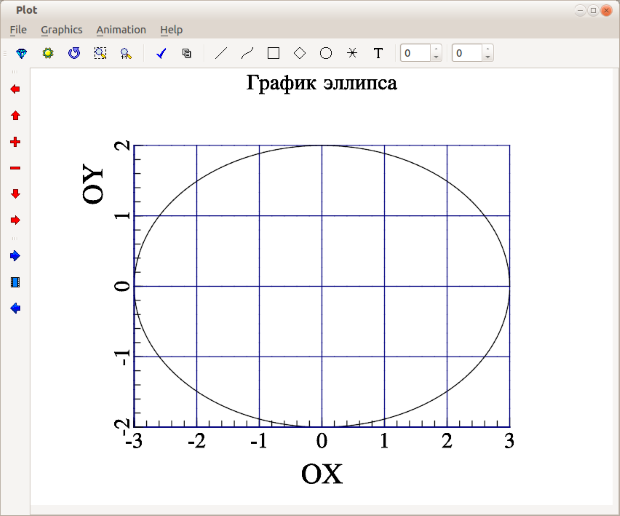
График задан в параметрической форме и представляет собой эллипс. Выберем интервал построения графика ![[0;2\cdot \pi]](/sites/default/files/tex_cache/ef39d6c21b0a48a6f0f0928396475c5e.png) , ранжируем переменную
, ранжируем переменную  на этом интервале, сформируем массивы
на этом интервале, сформируем массивы  и
и  и построим точечный график. Текст программы и результаты её работы (рис. B.7) представлены далее.
и построим точечный график. Текст программы и результаты её работы (рис. B.7) представлены далее.
#include <mgl2/qt .h>
#include <iostream>
#include <math.h>
using namespace std;
int sample ( mglGraph * gr )
{ //График эллипса
int i, n; float h, a, b, t;
a=0;
b=2*M_PI;
n=200;
h=(b-a ) /n;
//Формирование массивов абсцисс и ординат
mglData x ( n ), y ( n );
for ( i =0; i<n; i++)
{
t=a+ i *h;
x [ i ]=3* cos ( t );
y [ i ]=2* sin ( t );
}
gr->SetRanges ( -3,3, -2,2); //Границы по осям координат
gr->Axis ( ); //Оси координат
gr->Grid ( ); //Сетка
gr->Plot ( x, y, " k " ); //График функции
gr->set font size ( 2 );
gr->Title ( "График эллипса" );
gr->SetFontSsize ( 4 );
gr->Label ( " x ", " OX ", 0 );
gr->Label ( " y ", " OY " );
return 0;
}
int main ( int arg c, char ** argv )
{
set locale (LC_CTYPE, " ru_RU.utf 8 " );
mglQT gr ( sample, " Plot " );
return gr.Run ( );
}Задача B.7. Построить график функции:

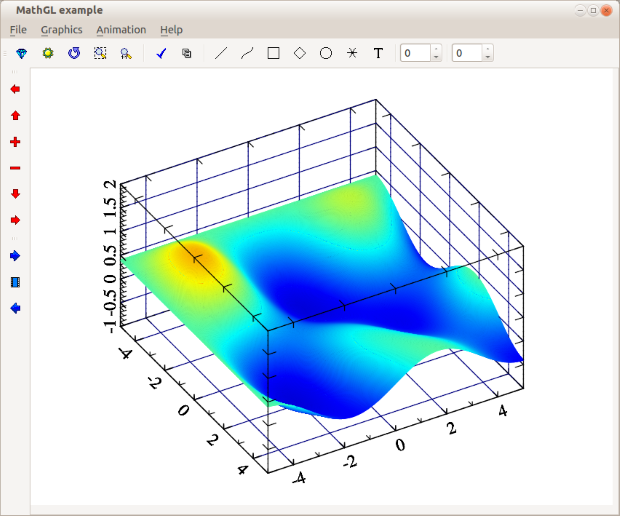
В данном случае необходимо построить график функции двух аргументов. Для этого нужно сформировать матрицу  при изменении значений аргументов
при изменении значений аргументов  и
и  и отобразить полученные результаты.
и отобразить полученные результаты.
Далее приведён текст программы и результаты её работы (рис. B.8).
#include <mgl2/qt .h>
#include <iostream>
using namespace std;
int sample ( mglGraph * gr )
{
//Изображение поверхности
gr->SetRanges ( -5,5, -5,5, -1,2); //Диапазон изменения x, y, z.
mglData z ( 500, 400 ); //Размер матрицы z по х и по y
//Формирование матрицы z.
z.Mod ify ( " 0.6 * sin ( 2 * pi * x ) * sin ( 3 * pi * y ) + 0.4 * cos ( 3 * pi *( x * y ) ) " );
gr->Rotate ( 40, 60 ); //Вращение осей
gr->Box ( );
gr->Axis ( );
gr->Grid ( );
gr->Mesh ( z ); //График функции
}
int main ( int arg c, char ** argv )
{
set locale (LC_CTYPE, " ru_RU.utf 8 " );
mglQT gr ( sample, " MathGL Example " );
return gr.Run ( );
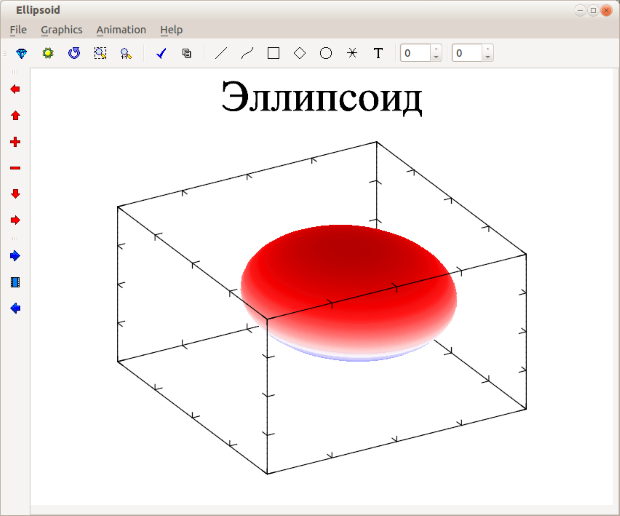
}Задача B.8.Построить эллипсоид.
Текст программы и результаты её работы (рис. B.9).
#include <mgl2/qt .h>
#include <mgl2/mgl .h>
#include <iostream>
using namespace std;
int sample ( mglGraph * gr )
{
gr->Title ( "Эллипсоид" );
mglData x ( 50, 40 ), y ( 50, 40 ), z ( 50, 40 );
gr->Fill ( x, " 0.1 + 0.8 * sin ( 2 * pi * x ) * sin ( 2 * pi * y ) " );
gr->Fill ( y, " 0.1 5 + 0.7 * cos ( 2 * pi * x ) * sin ( 2 * pi * y ) " );
gr->Fill ( z, " 0.2 + 0.6 * cos ( 2 * pi * y ) " );
gr->Rotate ( 50, 60 );
gr->Box ( );
gr->Surf ( x, y, z, " BbwrR " );
return 0;
}
int main ( int arg c, char ** argv )
{
set locale (LC_CTYPE, " ru_RU.utf 8 " );
mglQT gr ( sample, " Ellipse " );
return gr.Run ( );
}В завершении приведём решение реальной инженерной задачи с использованием MathGL.
Задача B.9. В "Основах химии" Д. И. Менделеева приводятся данные о растворимости азотнокислого натрия 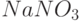 в зависимости от температуры воды. Число условных частей
в зависимости от температуры воды. Число условных частей 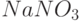 , растворяющихся в 100 частях воды при соответствующих температурах, представлено в таблице.
, растворяющихся в 100 частях воды при соответствующих температурах, представлено в таблице.
Требуется определить растворимость азотнокислого натрия при температурах 25, 32 и 45 градусов в случае линейной зависимости и найти коэффициент корреляции.
Параметры линейной зависимости (линии регрессии) 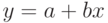 подбираются методом наименьших квадратов и рассчитываются по формулам
подбираются методом наименьших квадратов и рассчитываются по формулам
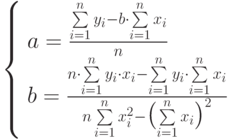
Этапы решения задачи:
- Ввод исходных данных из текстового файла.
- Вычисление параметров
 и
и  .
. - Расчёт значений линейной зависимости
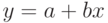 в точках 25, 32, 45.
в точках 25, 32, 45. - Изображение графиков: экспериментальных точек, линии регрессии и рассчитанных значений.
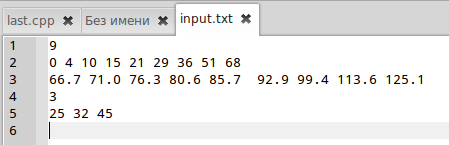
Исходные данные задачи хранятся в текстовом файле input.txt (см. рис. B.10).
В первой строке файла хранится количество экспериментальных точек, в следующих двух строках — массивы абсцисс и ординат экспериментальных точек. В четвёртой строке хранится количество (3) и точки (25, 32, 45), в которых необходимо вычислить ожидаемое значение.
Текст программы решения задачи с комментариями приведён ниже.
#include <mgl2/qt .h>
#include <iostream>
#include <fstream>
using namespace std;
int sample ( mglGraph * gr )
{
mglData x2 ( 70 ), y2 ( 70 );
int i, n, k;
float h, a, b, sx =0, sy =0, syx =0, sx2 =0;
ifstream f; //Поток для чтения файла исходных данных
f.open ( " input.txt " );
F>>n; //Чтение исходных данных, n — количество экспериментальных точек.
mglData x ( n ), y ( n ); //x(n),y(n) — координаты экспериментальных точек
cout<<" X \n ";
for ( i =0; i<n; i++)
{
F>>x [ i ];
cout<<x [ i ]<<" ";
}
cout<<endl;
cout<<" Y \n ";
for ( i =0; i<n; i++)
{
F>>y [ i ];
cout<<y [ i ]<<" ";
}
cout<<endl;
F>>k;
cout<<" k = "<<k<<endl;
mglData xr ( k ), yr ( k );
//xr, yr — ожидаемые значения,
for ( i =0; i<k; i++)
F>>xr [ i ];
cout<<endl;
for ( i =0; i<n; i++)
{
sx+=x [ i ];
sy+=y [ i ];
syx+=y [ i ] * x [ i ];
sx2+=x [ i ] * x [ i ];
}
//Расчёт коэффициентов линии регрессиии.
b=(n*syx-sy * sx ) / ( n*sx2-sx * sx );
a=(sy-b* sx ) /n;
cout<<" a = "<<a<<" b = "<<b<<endl;
//Формирование массивов для изображения линии регрессии на графике.
for ( i =0; i <70; i++)
{
x2 [ i ]=x [ i ]+ 1;
y2 [ i ]=a+b*x2 [ i ];
}
//Вычисление ожидаемых значений — растворимость азотнокислого натрия
//при температурах 25, 32 и 45 градусов.
cout<<" Xr Yr \n ";
for ( i =0; i<k; i++)
{
yr [ i ]=a+b* xr [ i ];
cout<<xr [ i ]<<" "<<yr [ i ]<< endl;
}
gr->SetRanges ( x [ 0 ], 80, 70, 140 );
gr->set font size ( 3 );
gr->Axis ( ); //Оси координат
gr->Grid ( ); //Сетка
//Первая легенда
gr->AddLegend ( "Эксперимент", " b o " );
gr->Plot ( x, y, " b o " ); //График экспериментальных точек, голубой (b) цвет.
//Вторая легенда
gr->AddLegend ( "Расчёт", " r * " );
gr->Plot ( xr, yr, " r * " ); //График ожидаемых значений.
//Третья легенда
gr->AddLegend ( "Линия регрессии", " k - " );
gr->Plot ( x2, y2, " k - " ); //Изображение линиии регрессии.
gr->Title ( "Задача Менделеева" ); //Заголовок
gr->Label ( " x ", " t ", 0 ); //Подпись по оси абсцисс
gr->Label ( " y ", " NaNO_3 " ); //Подпись по оси ординат
gr->Legend ( 2 ); //Вывод легенды
return 0;
}
int main ( int arg c, char ** argv )
{
set locale (LC_CTYPE, " ru_RU.utf 8 " );
mglQT gr ( sample, " Plot " );
return gr.Run ( );
}После запуска программы на экране пользователь увидит следующие значения
X 0 4 10 15 21 29 36 51 68 Y 66.7 71 76.3 80.6 85.7 92.9 99.4 113.6 125.1 k=3 a=67.5078 b=0.87064 Xr Yr 25 89.2738 32 95.3683 45 106.687
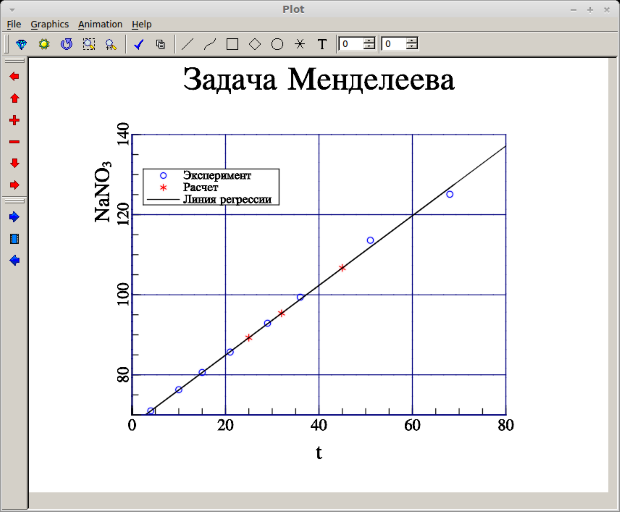
Графическое решение задачи, полученное с помощью средств библиотеки MathGL, представлено на рис. B.11.
Для изучения всех возможностей MathGL, авторы советуют обратиться к документации по MathGL. При освоении библиотеки MathGL следует помнить, что логика и синтаксис библиотеки напоминает синтаксис Scilab и Octave.