|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Использование компилятора командной строки и текстового редактора Geany
Одним из самых мощных современных кроссплатформенных компиляторов языка C++ является свободно-распространяемый компилятор g++. Для его установки в debian-подобных ОС семейства Linux (Debian, Ubuntu, Mint и их клоны) достаточно выполнить команду терминала apt-get install g++ с правами суперпользователя (администратора) или воспользоваться менеджером пакетов synaptic.
Установка компилятора g++ в ОС семейства Windows несколько сложнее, поэтому рассмотрим этот процесс более подробно.
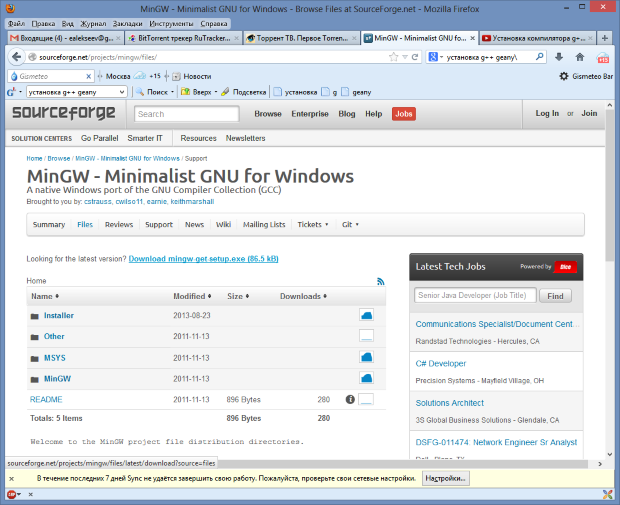
- На сайте mingw.org переходим в раздел Download (Загрузки), в появившемся окне щёлкаем по ссылке Download mingw-get-setup.exe (рис. A.1). Загружаем установочный файл и запускаем его.
- На первом этапе установки необходимо выбрать команду Install (см. рис. A.2), затем папку для установки (рис. A.3).
- После этого начнётся процесс доустановки инсталлятора (рис. A.4).
- Далее выбираем компиляторы для установки (C++, Fortran, Ada) (рис. A.5) и ждём пока будут скачаны и установлены необходимые компиляторы. После завершения процесса установки компиляторы (в нашем случае компилятор C++) готовы к использованию. Но для вызова их (из командной строки Windows, из текстового редактора Geany) необходимо указывать полное имя файла с компилятором. При установке компилятора C++ в стандартный каталог C:\MinGW — полное имя компилятора C++ будет таким: C:\MinGW\bin\g++. Для того, чтобы каждый раз не писать полное имя компилятора, можно добавить путь C:\MinGW\bin в список путей системной переменной Path.
- Для изменения значения системной переменной Path необходимо в панели управления выбрать Система -> Дополнительные параметры системы -> Дополнительно -> Переменные среды -> Системные переменные -> Path -> Изменить. В открывшемся диалоговом окне добавить путь C:\MinGW\bin\.
После перезагрузки ОС Windows для обращения к компилятору достаточно будет указывать его имя — g++.
Таким образом, в ОС Linux для работы с компилятором в командной строке необходимо запустить Терминал, а в ОС Windows – командную строку. После чего работа с компилятором g++ с ОС Windows и Linux идентична.
Рассмотрим опции компилятора командной строки, необходимые для компиляции и запуска простейших программ.
Для того, чтобы создать исполняемый файл из текста программы на C++, необходимо выполнить команду
g++ name.cpp
Здесь name.cpp — имя файла с текстом программы. В результате будет создан исполняемый файл со стандартным именем a.out. Для того, чтобы создать исполняемый файл с другим именем, необходимо выполнить команду
g++ -o nameout name.cpp
Здесь name.cpp — имя файла с текстом программы, nameout — имя исполняемого файла.
При использовании компилятора g++ после компиляции программы автоматически происходит компоновка программы (запуск компоновщика make). Чтобы исключить автоматическую компоновку программы, следует использовать опцию -c. В этом случае команда будет иметь вид g++ -c name.cpp
Технология работы с компилятором g++ может быть такой: набираем текст программы в стандартном текстовом редакторе, потом в консоли запускаем компилятор, после исправления синтаксических ошибок запускаем исполняемый файл. После каждого изменения текста программы надо сохранить изменения в файле на диске, запустить компилятор, и только после этого запускать программу (исполняемый файл). Очень важно не забывать сохранять текст программы, иначе при запуске компилятора будет компилироваться старая версия текста программы.
Компилятор g++ эффективен при разработке больших комплексов программ, он позволяет собирать приложения из нескольких файлов, создавать библиотеки программ. Рассмотрим процесс создания и использования библиотеки решения задач линейной алгебры (см. п. 6.4, задачи 6.10 — 6.12):
int SLAU(double **matrica_a, int n, double *massiv_b, double *x) — функция решения системы линейных алгебраических уравнений;
int INVERSE(double **a, int n, double **y) — функция вычисления обратной матрицы;
double determinant(double **matrica_a, int n) — функция вычисления определителя.
Для создания библиотеки создадим заголовочный файл slau.h и файл slau.cpp, в который поместим тексты всех трёх функций решения задач линейной алгебры.
Текст файла slau1.h:
int SLAU( double ** matrica_a, int n, double *massiv_b, double *x ); int INVERSE( double **a, int n, double **y ); double determinant ( double ** matrica_a, int n );
Текст файла slau1.cpp:
#include <math.h>
int SLAU( double ** matrica_a, int n, double *massiv_b, double *x )
{
int i, j, k, r;
double c,M, max, s;
double **a, *b;
a=new double * [ n ];
for ( i =0; i<n; i++)
a [ i ]=new double [ n ];
b=new double [ n ];
for ( i =0; i<n; i++)
for ( j =0; j<n; j++)
a [ i ] [ j ]=matrica_a [ i ] [ j ];
for ( i =0; i<n; i++)
b [ i ]=massiv_b [ i ];
for ( k=0;k<n; k++)
{
max=fabs ( a [ k ] [ k ] );
r=k;
for ( i=k+1; i<n; i++)
if ( fabs ( a [ i ] [ k ] )>max)
{
max=fabs ( a [ i ] [ k ] );
r= i;
}
for ( j =0; j<n; j++)
{
c=a [ k ] [ j ];
a [ k ] [ j ]=a [ r ] [ j ];
a [ r ] [ j ]= c;
}
c=b [ k ];
b [ k ]=b [ r ];
b [ r ]= c;
for ( i=k+1; i<n; i++)
{
for (M=a [ i ] [ k ] / a [ k ] [ k ], j=k; j<n; j++)
a [ i ] [ j ]-=M*a [ k ] [ j ];
b [ i ]-=M*b [ k ];
}
}
if ( a [ n -1 ] [ n-1]==0)
if ( b [ n-1]==0)
return -1;
else return -2;
else
{
for ( i=n-1; i >=0; i --)
{
for ( s =0, j= i +1; j<n; j++)
s+=a [ i ] [ j ] * x [ j ];
x [ i ]=( b [ i ]- s ) / a [ i ] [ i ];
}
return 0;
}
}
int INVERSE( double **a, int n, double **y )
{
int i, j, res;
double *b, *x;
b=new double [ n ];
x=new double [ n ];
for ( i =0; i<n; i++)
{
for ( j =0; j<n; j++)
if ( j==i )
b [ j ]= 1;
else b [ j ]= 0;
res=SLAU( a, n, b, x );
if ( res !=0)
break;
else
for ( j =0; j<n; j++)
y [ j ] [ i ]=x [ j ];
}
if ( res !=0)
return -1;
else
return 0;
}
double determinant ( double ** matrica_a, int n )
{
int i, j, k, r;
double c,M, max, s, det =1;
double **a;
a=new double * [ n ];
for ( i =0; i<n; i++)
a [ i ]=new double [ n ];
for ( i =0; i<n; i++)
for ( j =0; j<n; j++)
a [ i ] [ j ]=matrica_a [ i ] [ j ];
for ( k=0;k<n; k++)
{
max=fabs ( a [ k ] [ k ] );
r=k;
for ( i=k+1; i<n; i++)
if ( fabs ( a [ i ] [ k ] )>max)
{
max=fabs ( a [ i ] [ k ] );
r= i;
}
if ( r !=k ) det=_det;
for ( j =0; j<n; j++)
{
c=a [ k ] [ j ];
a [ k ] [ j ]=a [ r ] [ j ];
a [ r ] [ j ]= c;
}
for ( i=k+1; i<n; i++)
for (M=a [ i ] [ k ] / a [ k ] [ k ], j=k; j<n; j++)
a [ i ] [ j ]_=M_a [ k ] [ j ];
}
for ( i =0; i<n; i++)
det*=a [ i ] [ i ];
return det;
for ( i =0; i<n; i++)
delete [ ] a [ i ];
delete [ ] a;
}В качестве тестовой задачи напишем главную функцию, которая предназначена для решения системы линейных алгебраических уравнений.
#include <iostream>
#include <math.h>
//Подключение личной библиотеки slau
#include " slau1 .h "
using namespace std;
int main ( )
{
int result, i, j,N;
double **a, *b, *x;
//Ввод размерности системы.
cout<<" N = ";
cin>>N;
//Выделение памяти для матрицы правых частей и вектора свободных членов.
a=new double * [N ];
for ( i =0; i<N; i++)
a [ i ]=new double [N ];
b=new double [N ];
x=new double [N ];
//Ввод матрицы правых частей и вектора свободных членов .
cout<<" Input Matrix A "<<endl;
for ( i =0; i<N; i++)
for ( j =0; j<N; j++)
cin>>a [ i ] [ j ];
cout<<" Input massiv B "<<endl;
for ( i =0; i<N; i++)
cin>>b [ i ];
//Вызов функции решения СЛАУ методом Гаусса из библиотеки slau.h
result=SLAU( a,N, b, x );
if ( result ==0)
{
//Вывод массива решения.
cout<<" MassivX "<<endl;
for ( i =0; i<N; i++)
cout<<x [ i ]<<" \t ";
cout<<endl;
}
else if ( result ==-1)
cout<<"Бесконечное множество решений\n ";
else if ( result ==-2)
cout<<"Нет решений\n ";
}Теперь необходимо из этих текстов создать работающее приложение. Рассмотрим это поэтапно.
- Компиляция библиотеки slau1.h с помощью команды g++ -c slau1.cpp.
- Компиляция главной функции main.cpp с помощью команды g++ -c main.cpp.
- Создание исполняемого файла с именем primer из двух откомпилированных файлов main.o и slau1.o с помощью команды g++ main.o slau1.o -o primer.
- Запуск исполняемого файла.
После разработки библиотеки линейной алгебры (пример) slau1, можно использовать её в различных программах при вычислении определителя, обратной матрицы и решения систем линейных алгебраических уравнений.
При разработке программ с большим количеством вычислений, компилятор g++ позволяет оптимизировать программы по быстродействию. Для получения оптимизированных программ можно использовать ключи -O0, -O1, -O2, -O3, -Os:
- при использовании ключа -O0 оптимизация отключена, достигается максимальная скорость компиляции, опция задействована по умолчанию;
- при использовании ключа "мягкой" оптимизации -O1 происходит некоторое увеличение времени компиляции, этот ключ оптимизации позволяет одновременно уменьшать занимаемую программой память и уменьшить время выполнения программы;
- при использовании ключа -02 происходит существенное уменьшение времени работы программы, при этом не происходит увеличение памяти, занимаемой программой, не происходит развёртка циклов и автоматическое встраивание функций;
- ключ "агрессивной" оптимизации -O3 нацелен в первую очередь на уменьшение времени выполнения программы, при этом может произойти увеличение объёма кода и времени компиляции, в этом случае происходит развёртка циклов и автоматическое встраивание функций;
- ключ -Os ориентирован на оптимизацию размера программы, включаются те опции из набора -O2, которые обычно не увеличивают объём кода, применяются некоторые другие оптимизации, направленные на снижение его объёма.
Для разработки программ на различных языках программирования можно использовать текстовый редактор Geany. Редактор Geany входит в репозитории большинства дистрибутивов Linux, его установка осуществляется стандартным для вашего дистрибутива образом (в debian-подобных ОС с помощью команды apt-get install geany). Для установки его в Windows необходимо скачать со страницы http://www.geany.org/Download/Releases инсталляционный файл и установить программу стандартным способом.
Разработка программ с использованием Geany более эффективна. Окно Geany представлено на рис. A.6.
Последовательно рассмотрим основные этапы разработки программы с использованием Geany.
- Необходимо создать шаблон приложения на C/C++ (или другом языке программирования) с помощью команды Файл -> Создать из шаблона -> main.cxx. После чего необходимо ввести текст программы и сохранить его.
- Для компиляции и запуска программы на выполнение служит пункт меню Сборка. Для компиляции программы следует использовать команду Сборка -> Скомпилировать (F8). В этом случае будет построен объектный код программы (файл с расширением .o или .obj). Для создания исполняемого кода программы служит команда Сборка -> Собрать (Shift+F9). Для запуска программы следует выполнить команду Сборка -> Выполнить (F5).
Параметры компилятора определяются автоматически после выбора шаблона (Файл -> Создать из шаблона). Однако команды компиляции и сборки по умолчанию можно изменить, используя команду Сборка -> Установить параметры сборки (см. рис. A.7). Здесь %f — имя компилируемого файла, %e — имя файла без расширения.