НОУ ИНТУИТ | Программирование на языке С++ в среде Qt Creator. Лекция 6: Статические и динамические матрицы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 07.03.2015 | Доступ: свободный | Студентов: 2201 / 531 | Длительность: 24:14:00

Тема: Программирование

Специальности: Программист, Архитектор программного обеспечения

|

Вам нравится? Нравится 77 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.4 Решение некоторых задач линейной алгебры

В этом параграфе рассмотрим использование матриц при решении таких задач линейной алгебры, как сложение, вычитание и умножение матриц, решение систем линейных алгебраических уравнений, вычисление определителя и обратной матрицы.

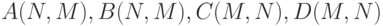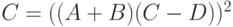Задача 6.9.Заданы четыре матрицы вещественных чисел A(N,M), B(N,M), C(M,N), D(M,N) . Вычислить матрицу C=((A+B)(C-D))^2 .

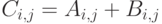Суммой (разностью) матриц одинаковой размерности и называется матрица , элементы которой получаются сложением $C_{i,j}=A_{i,j}+B_{i,j}$ (вычитанием 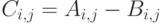$C_{i,j}=A_{i,j}-B_{i,j}$ ) соответствующих элементов исходных матриц.

Напомним алгоритм умножения матриц на примере

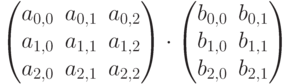
$\small $\left(\begin{matrix}a_{0,0}&a_{0,1}&a_{0,2}\\a_{1,0}&a_{1,1}&a_{1,2}\\a_{2,0}&a_{2,1}&a_{2,2}\end{matrix}\right)\cdot \left(\begin{matrix}b_{0,0}&b_{0,1}\\b_{1,0}&b_{1,1}\\b_{2,0}&b_{2,1}\end{matrix}\right)$

Воспользовавшись правилом "строка на столбец", получим матрицу:

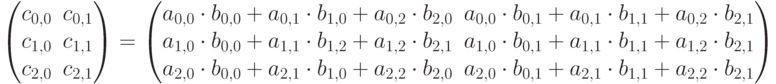
$\left(\begin{matrix}c_{0,0}&c_{0,1}\\c_{1,0}&c_{1,1}\\c_{2,0}&c_{2,1}\end{matrix}\right)= \left(\begin{matrix}a_{0,0}\cdot b_{0,0}+a_{0,1}\cdot b_{1,0}+a_{0,2}\cdot b_{2,0}&a_{0,0}\cdot b_{0,1}+a_{0,1}\cdot b_{1,1}+a_{0,2}\cdot b_{2,1}\\a_{1,0}\cdot b_{0,0}+a_{1,1}\cdot b_{1,2}+a_{1,2}\cdot b_{2,1}&a_{1,0}\cdot b_{0,1}+a_{1,1}\cdot b_{1,1}+a_{1,2}\cdot b_{2,1}\\a_{2,0}\cdot b_{0,0}+a_{2,1}\cdot b_{1,0}+a_{2,2}\cdot b_{2,0}&a_{2,0}\cdot b_{0,1}+a_{2,1}\cdot b_{1,1}+a_{2,2}\cdot b_{2,1}\end{matrix}\right)$

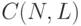Произведением матриц A(N,M) и B(M,L) является матрица C(N,L) , каждый элемент которой 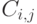$C_{i,j}$ вычисляется по формуле:

$C_{i,j}=\sum\limits_{k=0}^{M-1}A_{i,k}B_{k,j}$

где

и

.

Операция умножения имеет смысл только в том случае, если количество строк левой матрицы совпадает с количеством столбцов правой. Кроме того, 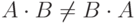$A\cdot B\neq B\cdot A$ .

При решении задачи будем использовать динамические матрицы и двойные указатели. Напишем следующие функции.

float **sum_m(float **A, float **B, int N, int M) — функция формирует матрицу, которая является суммой двух матриц. Здесь A, B — указатели на исходные матрицы, N, M — количество строк и столбцов матриц, функция возвращает указатель на сформированную матрицу, которая является суммой двух матриц и .
float **minus_m(float **A, float **B, int N, int M) — функция формирует матрицу, которая является разностью двух матриц. Здесь A, B — указатели на исходные матрицы, N, M — количество строк и столбцов матриц, функция возвращает указатель на сформированную матрицу, которая является разностью двух матриц и .
float **product_m(float **A, float **B, int N, int M, int L) — функция формирует матрицу, которая является произведением двух матриц. Здесь A, B — указатели на исходные матрицы. Матрица имеет строк и столбцов, матрица имеет строка и столбцов, функция возвращает указатель на сформированную матрицу, которая является произведением двух матриц и .
float **create_m(int N, int M) — функция создаёт матрицу, в которой будет строк и столбцов, осуществляет ввод элементов матрицы, функция возвращает указатель на сформированную матрицу.
void output_m(float **A, int N, int M) — функция построчного вывода на экран матрицы , которая имеет строк и столбцов.

Далее приведён текст программы с комментариями.

#include <iostream>
using namespace std;
//функция вычисления суммы двух матриц.
float **sum_m( float **A, float **B, int N, int M)
{
	int i, j;
	float **temp; //указатель для хранения результирующей матрицы
	temp=new float * [N ]; //выделение памяти для хранения результирующей матрицы
	for ( i =0; i<N; i++)
		temp [ i ]=new float [M];
	for ( i =0; i<N; i++) //Вычисляем сумму двух матриц
		for ( j =0; j<M; j++)
			temp [ i ] [ j ]=A [ i ] [ j ]+B [ i ] [ j ];
	return temp; //Возвращаем матрицу как двойной указатель
}
//функция вычисления разности двух матриц.
float **minus_m ( float **A, float **B, int N, int M)
{ int i, j;
	float **temp; //указатель для хранения результирующей матрицы
	temp=new float * [N ]; //выделение памяти для хранения результирующей матрицы
	for ( i =0; i<N; i++)
		temp [ i ]=new float [M];
	for ( i =0; i<N; i++) //Вычисляем разность двух матриц
		for ( j =0; j<M; j++)
			temp [ i ] [ j ]=A [ i ] [ j ]-B [ i ] [ j ];
	return temp; //Возвращаем матрицу как двойной указатель
}
//функция вычисления произведения двух матриц.
float **product_m ( float **A, float **B, int N, int M, int L)
{
	int i, j, k;
	float **temp; //указатель для хранения результирующей матрицы
	temp=new float * [N ]; //выделение памяти для хранения результирующей матрицы
	for ( i =0; i<N; i++)
		temp [ i ]=new float [ L ];
	//Вычисляем произведение двух матриц, последовательно формируя все элементы матрицы
	for ( i =0; i<N; i++)
		for ( j =0; j<L; j++)
			//Элемент с индексами i, j — скалярное произведение i-й строки матрицы A
			for ( temp [ i ] [ j ]=k=0;k<M; k++) //и j-го столбца матрицы B
				temp [ i ] [ j ]+=A [ i ] [ k ] *B [ k ] [ j ];
	return temp; //Возвращаем матрицу как двойной указатель
}
//функция создаёт динамическую матрицу вещественных чисел размерности N на M,
//в этой же функции осуществляется и ввод элементов матрицы
float ** create_m ( int N, int M)
{
	int i, j;
	float **temp;
	temp=new float * [N ];
	for ( i =0; i<N; i++)
		temp [ i ]=new float [M];
	cout<<"Ввод матрицы\n ";
	for ( i =0; i<N; i++)
		for ( j =0; j<M; j++)
			cin>>temp [ i ] [ j ];
	return temp;
}
//функция осуществляет построчный вывод матрицы A(N,M)
void output_m ( float **A, int N, int M)
{
	int i, j;
	//Цикл по строкам. По окончанию вывода всех элементов строки — переход на новую строку.
	for ( i =0; i<N; cout<<endl, i++)
		for ( j =0; j<M; j++) //Цикл по переменной j, в котором перебираем строки матрицы
			cout<<A [ i ] [ j ]<<" \t "; //Вывод очередного элемента матрицы и символа табуляции.
}
int main ( int arg c, char ** argv )
{
	float **A, **B, **C, **D, ** result; //указатели для хранения исходных и
	результирующей матриц
	int N,M;
	cout<<" N = "; cin>>N; //Ввод размерностей матрицы
	cout<<" M = "; cin>>M;
	//Выделение памяти и ввод матриц A, B, C, D, обращением к функции create_m.
	A=create_m (N,M);
	B=create_m (N,M);
	C=create_m (M,N);
	D=create_m (M,N);
	//Вычисление результирующей матрицы.
	result=product_m ( product_m (sum_m(A, B,N,M),minus_m (C,D,M,N),N,M,N), product_m
		(sum_m(A, B,N,M),minus_m (C,D,M,N),N,M,N),N,N,N);
	output_m ( result,N,N); //Вывод результирующей матрицы.
	return 0;
}

Далее без комментариев приведена программа решения задачи 6.9 с помощью динамических матриц и обычных указателей^{3Обращаем внимание читателя, что при использовании одинарных указателей обращение к элементам матрицы происходит быстрее. При обработке матриц большой размерности (более 1000000 элементов) имеет смысл использовать именно одинарные указатели для хранения и обработки матриц. Это позволит ускорить работу программ на 10-15%.}. Рекомендуем читателям самостоятельно разобраться с этой версией программы.

#include <iostream>
using namespace std;
float *sum_m( float *A, float *B, int N, int M)
{
	int i, j;
	float *temp;
	temp=new float [N*M];
	for ( i =0; i<N; i++)
		for ( j =0; j<M; j++)
			temp [ i *M+j ]=A [ i *M+j ]+B [ i *M+j ];
	return temp;
}
float *minus_m ( float *A, float *B, int N, int M)
{ int i, j;
	float *temp;
	temp=new float [N*M];
	for ( i =0; i<N; i++)
		for ( j =0; j<M; j++)
			temp [ i *M+j ]=A [ i *M+j ]-B [ i *M+j ];
	return temp;
}
float *product_m ( float *A, float *B, int N, int M, int L)
{
	int i, j, k;
	float *temp;
	temp=new float [N*L ];
	for ( i =0; i<N; i++)
		for ( j =0; j<L; j++)
			for ( temp [ i *L+j ]=k=0;k<M; k++)
				temp [ i *L+j ]+=A [ i *M+k ] *B [ k*L+j ];
	return temp;
}
float *create_m ( int N, int M)
{
	int i, j;
	float *temp;
	temp=new float [N*M];
	cout<<"Ввод матрицы\n ";
	for ( i =0; i<N; i++)
		for ( j =0; j<M; j++)
			cin>>temp [ i *M+j ];
	return temp;
}
void output_m ( float *A, int N, int M)
{
	int i, j;
	for ( i =0; i<N; cout<<endl, i++)
		for ( j =0; j<M; j++)
			cout<<A [ i *M+j ]<<" \t ";
}
int main ( int arg c, char ** argv )
{
	float *A, *B, *C, *D, * result;
	int N,M;
	cout<<" N = "; cin>>N;
	cout<<" M = "; cin>>M;
	A=create_m (N,M);
	B=create_m (N,M);
	C=create_m (M,N);
	D=create_m (M,N);
	result=product_m ( product_m (sum_m(A, B,N,M), minus_m (C,D,M,N),N,M,N),
		product_m (sum_m(A, B,N,M), minus_m (C,D,M,N),N,M,N),N,N,N);
	output_m ( result,N,N);
	return 0;
}

Дальше >>

Авторизоваться

Программирование на языке С++ в среде Qt Creator

Статические и динамические матрицы

6.4 Решение некоторых задач линейной алгебры

Вопросы и ответы