|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Статические и динамические матрицы
Задача 6.11. Найти обратную матрицу к квадратной матрице 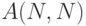 .
.
Один из методов вычисления обратной матрицы основан на решении систем линейных алгебраических уравнений. Пусть задана некоторая матрица  :
:
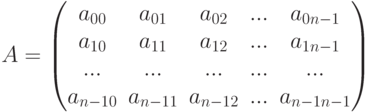 |
( 6.5) |
Необходимо найти матрицу 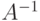 , которая является обратной к матрице
, которая является обратной к матрице  :
:
 |
( 6.6) |
Матрица (6.6) будет обратной к матрице (6.5), если выполняется соотношение
 , где
, где  — это единичная матрица, или более подробно:
— это единичная матрица, или более подробно:
 |
( 6.7) |
Результат перемножения матриц из соотношения (6.7) можно представить поэлементно в виде  систем линейных уравнений. Умножение матрицы (6.5) на нулевой столбец матрицы (6.6) даст нулевой столбец единичной матрицы:
систем линейных уравнений. Умножение матрицы (6.5) на нулевой столбец матрицы (6.6) даст нулевой столбец единичной матрицы:

При умножении матрицы  на первый столбец обратной матрицы получается следующая система линейных алгебраических уравнений.
на первый столбец обратной матрицы получается следующая система линейных алгебраических уравнений.
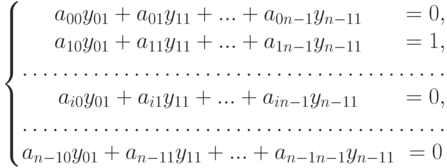
Система, полученная в результате умножения матрицы (6.5) на  -й столбец матрицы (6.6), будет выглядеть следующим образом:
-й столбец матрицы (6.6), будет выглядеть следующим образом:

Понятно, что  -я система будет иметь вид:
-я система будет иметь вид:
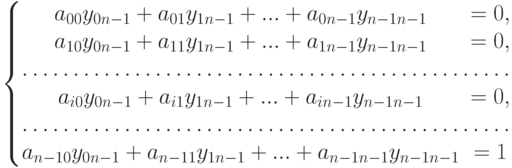
Решением каждой из приведённых выше систем будет  -й столбец обратной матрицы. Количество систем равно размерности обратной матрицы. Для отыскания решений систем линейных алгебраических уравнений можно воспользоваться методом Гаусса.
-й столбец обратной матрицы. Количество систем равно размерности обратной матрицы. Для отыскания решений систем линейных алгебраических уравнений можно воспользоваться методом Гаусса.
Описанный алгоритм представлен в виде блок-схемы на рис. 6.15. Блоки 2–5 отражают формирование вектора правых частей системы линейных алгебраических уравнений. Если условие в блоке 3 выполняется и элемент находится на главной диагонали, то он равен единице, все остальные элементы нулевые. В блоке 6 происходит вызов подпрограммы для решения системы уравнений методом Гаусса. В качестве параметров в эту подпрограмму передаётся исходная матрица  , сформированный в блоках 2–5 вектор свободных коэффициентов
, сформированный в блоках 2–5 вектор свободных коэффициентов  , размерность системы
, размерность системы  . Вектор
. Вектор  будет решением
будет решением  -й системы уравнений и, следовательно,
-й системы уравнений и, следовательно,  -м столбцом искомой матрицы
-м столбцом искомой матрицы  .
.
Как видно из блок-схемы, приведённой на рис. 6.15, при нахождении обратной матрицы понадобится функция SLAU, рассмотренная при решении задачи 6.10. Ниже приведён текст программы с подробными комментариями решения задачи 6.11. В функции main() будет находиться ввод исходной матрицы, обращение к функции INVERSE для вычисления обратной матрицы. Из функции INVERSE будет осуществляться вызов функции SLAU для решения системы линейных алгебраических уравнений.
#include <iostream>
#include <math.h>
using namespace std;
//Функция решения системы линейных алгебраических уравнений методом Гаусса.
int SLAU( double ** matrica_a, int n, double *massiv_b, double *x )
{
int i, j, k, r;
double c,M, max, s;
double **a, *b;
a=new double * [ n ];
for ( i =0; i<n; i++)
a [ i ]=new double [ n ];
b=new double [ n ];
for ( i =0; i<n; i++)
for ( j =0; j<n; j++)
a [ i ] [ j ]=matrica_a [ i ] [ j ];
for ( i =0; i<n; i++)
b [ i ]=massiv_b [ i ];
for ( k=0;k<n; k++)
{
max=fabs ( a [ k ] [ k ] );
r=k;
for ( i=k+1; i<n; i++)
if ( fabs ( a [ i ] [ k ] )>max)
{
max=fabs ( a [ i ] [ k ] );
r= i;
}
for ( j =0; j<n; j++)
{
c=a [ k ] [ j ];
a [ k ] [ j ]=a [ r ] [ j ];
a [ r ] [ j ]= c;
}
c=b [ k ];
b [ k ]=b [ r ];
b [ r ]= c;
for ( i=k+1; i<n; i++)
{
for (M=a [ i ] [ k ] / a [ k ] [ k ], j=k; j<n; j++)
a [ i ] [ j ]*=M_a [ k ] [ j ];
b [ i ]_=M_b [ k ];
}
}
if ( a [ n -1 ] [ n-1]==0)
if ( b [ n-1]==0)
return -1;
else return -2;
else
{
for ( i=n-1; i >=0; i --)
{
for ( s =0, j= i +1; j<n; j++)
s+=a [ i ] [ j ] * x [ j ];
x [ i ]=( b [ i ]- s ) / a [ i ] [ i ];
}
return 0;
}
for ( i =0; i<n; i++)
delete [ ] a [ i ];
delete [ ] a;
delete [ ] b;
}
//Функция вычисления обратной матрицы
int INVERSE( double **a, int n, double **y )
//Формальные параметры: a — исходная матрица, n — размерность матрицы, y — обратная
матрица.
//Функция будет возвращать 0, если обратная матрица существует, -1 — в противном случае.
{
int i, j, res;
double *b, *x;
//Выделение памяти для промежуточных массивов b и x.
b=new double [ n ];
x=new double [ n ];
for ( i =0; i<n; i++)
{
//Формирование вектора правых частей для нахождения i-го столбца матрицы.
for ( j =0; j<n; j++)
if ( j==i )
b [ j ]= 1;
else b [ j ]= 0;
//Нахождение i-го столбца матрицы путём решения СЛАУ Ax = b методом Гаусса.
res=SLAU( a, n, b, x );
//Если решение СЛАУ не найдено, то невозможно вычислить обратную матрицу.
if ( res !=0)
break;
else
//Формирование i-го столбца обратной матрицы.
for ( j =0; j<n; j++)
y [ j ] [ i ]=x [ j ];
}
//Проверка существования обратной матрицы, если решение одного из уравнений Ax=b не
//существует, то невозможно найти обратную матрицу, и функция INVERSE вернёт значение -1.
if ( res !=0)
return -1;
//Если обратная матрица найдена, то функция INVERSE вернёт значение 0,
//а обратная матрица будет возвращаться через указатель double **y.
else
return 0;
}
int main ( )
{
int result, i, j,N;
double **a, **b; //Двойные указатели для хранения исходной a и обратной b матрицы.
cout<<" N = "; //Ввод размера матрицы.
cin>>N;
a=new double * [N ]; //Выделение памяти для матриц a и b.
for ( i =0; i<N; i++)
a [ i ]=new double [N ];
b=new double * [N ];
for ( i =0; i<N; i++)
b [ i ]=new double [N ];
cout<<"Ввод матрицы A "<<endl; //Ввод исходной матрицы.
for ( i =0; i<N; i++)
for ( j =0; j<N; j++)
cin>>a [ i ] [ j ];
result=INVERSE( a,N, b ); //Вычисление обратной матрицы.
if ( result ==0) //Если обратная матрица существует, то вывести её на экран.
{
cout<<"Обратная матрица"<<endl;
for ( i =0; i<N; cout<<endl, i++)
for ( j =0; j<N; j++)
cout<<b [ i ] [ j ]<<" \t ";
}
else
//Если обратная матрица не существует, то вывести соответствующее сообщение.
cout<<"Нет обратной матрицы"<<endl;
}