Краткий обзор алгоритмов интеллектуального анализа данных. Алгоритмы временных рядов и кластеризации
Анализ временных рядов
В общем случае, временной ряд - это набор числовых значений, собранных в последовательные моменты времени (в большинстве случаев - через равные промежутки времени). В качестве примера можно назвать котировки иностранных валют или других биржевых товаров, результаты серии экспериментов и т.п. Целью анализа временного ряда может быть выявление имеющихся зависимостей текущих значений параметров от предшествующих и последующее их использование для прогнозирования новых значений.
Ряд можно представить как упорядоченное множество элементов или событий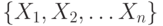 
, каждое из которых в общем случае может быть описано набором атрибутов: 
.Но на практике чаще всего используется один атрибут. При описании варианта для интеллектуального анализа данных, отметка времени (или номер элемента во временном ряде) вводится как один из атрибутов. Как правило, предполагается, что отметка времени - дискретное числовое значение, а предсказываемый атрибут(ы) - непрерывный.
Выделяют два основных формата представления временных рядов - столбчатый и чередующийся(англ. mixed) [1]. Пусть рассматриваемая предметная область - торговля велосипедами. И нужно представить данные по продажам двух моделей велосипедов по месяцам, модели называются M200 и R200.В этом случае мы имеем два временных ряда. В таблице 10.1 они представлены в столбчатом формате, в таблице 10.2 - используется чередующийся.
| Год и месяц | Количество M200 | КоличествоR200 |
|---|---|---|
| 200904 | 100 | 50 |
| 200905 | 120 | 20 |
| 200906 | 110 | 60 |
| … | … | … |
| Год и месяц | Модель | Количество |
|---|---|---|
| 200904 | M200 | 100 |
| 200904 | R200 | 50 |
| 200905 | M200 | 120 |
| 200905 | R200 | 20 |
| 200906 | M200 | 110 |
| 200906 | R200 | 60 |
| … | … | … |
С данными в столбчатом формате несколько проще работать, но этот формат менее гибкий. В приведенном примере, если с какого-то момента появилась в продаже третья модель велосипеда, добавить данные о ней в случае использования чередующегося формата будет проще.
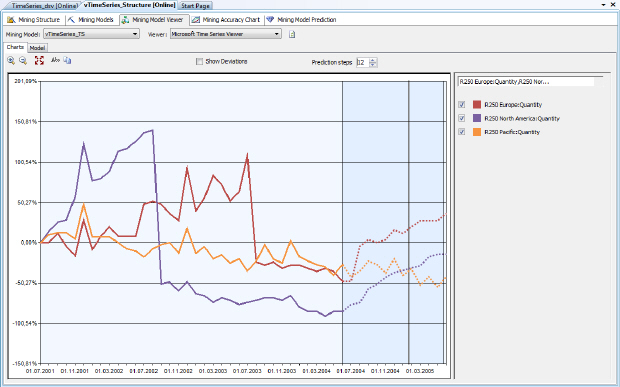
Фактические значения элементов ряда используются для обучения модели, после чего делается попытка прогноза для указанного числа новых элементов. Пример подобного анализа представлен на рис. 10.1, где пунктирной линией изображены предсказываемые значения.
Рассмотрим теперь некоторые особенности реализации алгоритма в SQLServer 2008. Алгоритм временных рядов Майкрософт (MicrosoftTimeSeries) предоставляет собой совокупность двух алгоритмов регрессии, оптимизированных для прогноза рядов непрерывных числовых значений. Этими алгоритмами являются:
- "дерево авторегрессии с перекрестным прогнозированием" (ARTxp), который оптимизирован для прогнозирования следующего значения в ряду;появился в SQL Server 2005;
- "интегрированные скользящие средние авторегрессии" (ARIMA), являющийся отраслевым стандартом в данной области; добавлен в SQL Server 2008, чтобы повысить точность долгосрочного прогнозирования.
По умолчанию службы AnalysisServices используют каждый алгоритм отдельно для обучения модели, а затем объединяют результаты, чтобы получить самый лучший прогноз. Также можно выбрать для использования только один алгоритм, в зависимости от имеющихся данных и требований к прогнозам.
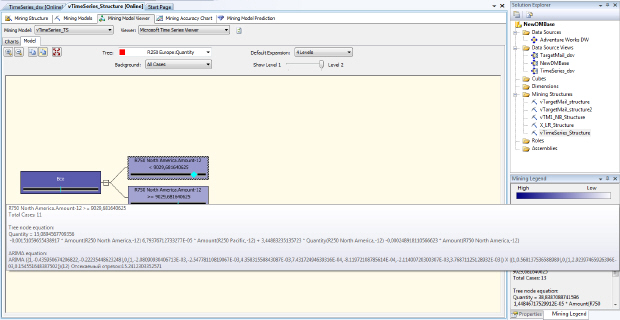
На рис. 10.2 представлены параметры для одного из узлов прогнозирующей модели, основанной на алгоритме временных рядов. Из рисунка видно, что узел на самом деле содержит параметры для двух алгоритмов. Также у рассматриваемого временного ряда 'R250 Europe: Quantity' (количество проданных в Европе велосипедов марки R250) обнаружена корреляция с другим рядом 'R750 NorthAmerica: Amount' (продажи в Северной Америке велосипедов марки R750).
Учет корреляций между рассматриваемыми рядами или, иначе говоря, перекрестного влияния, можно отметить в качестве особенности реализации алгоритма временных рядов в SQLServer. Это может быть важно, если одновременно анализируются связанные ряды, например, описывающие цены на нефть и котировки валют нефтедобывающих стран. Данную полезную возможность поддерживает только алгоритм ARTxp. Если для прогноза используется только алгоритм ARIMA, перекрестное влияние рядов не учитывается.
Точность прогноза для временного ряда может повысить указание известной периодичности. Например, в данных о продажах магазина спорттоваров по месяцам, скорее всего, будет присутствовать периодичность 12 (по числу месяцев в году).
Кратко рассмотрим основную идею метода авторегрессии. Авторегрессия отличается от обычной регрессии тем, что текущее значение параметра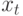 
выражается через его значения в предыдущие моменты времени. Если использовать линейные зависимости, то алгоритм ищет решение в виде:
где 
- погрешность, которую надо минимизировать путем подбора коэффициентов 
, в чем и заключается обучение модели. Как видно из
рис.
10.2, наличие корреляции может учитываться путем включения в эту формулу членов из другого ряда. Периодичность учитывают, вводя в рассмотрение дополнительные члены последовательности. Например, для периодичности 12 это будет 
, 
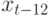и т.д. А использование аналитическими службами SQLServer дерева авторегрессии позволяет менять формулу путем разбиения в точках нелинейности.
Кластеризация
Как мы уже разбирали ранее, кластеризация позволяет снизить размерность задачи анализа предметной области, путем "естественной" группировки вариантов в кластеры. Таким образом, кластер будут объединять близкие по совокупности параметров элементы, и в некоторых случаях его можно рассматривать как единое целое. Например, описывая какой-то курортный регион можно сказать в нем 250 дней в году хорошая погода, не вдаваясь в подробности относительно температуры, атмосферного давления и т.д.
В случаях, когда для группировки используются значения 1-2 параметров, задача кластеризации может быть относительно быстро решена вручную или, например, обычными средствами работы с реляционными БД. Когда параметров много, возникает потребность в автоматизации процесса выявления кластеров.
Предоставляемый аналитическими службами SQL Server 2008 алгоритм кластеризации(MicrosoftClustering), использует итерационные методы для группировки вариантов со сходными характеристиками в кластеры. Алгоритм сначала определяет имеющиеся связи в наборе данных и на основе этой информации формирует кластеры.
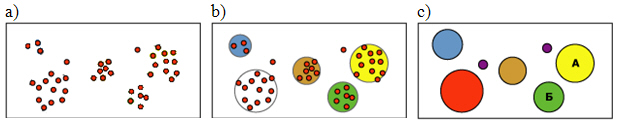
Идею можно проиллюстрировать с помощью диаграмм на рис. 10.3. На первом этапе ( рис. 10.3a) имеется множество вариантов, далее ( рис. 10.3b) идет итерационный процесс формирования кластеров, и в итоге относительно небольшой набор кластеров, которым можно задать идентификаторы и продолжить анализ.
MicrosoftClustering содержит реализацию двух алгоритмов кластеризации. Первый из них, алгоритм К-средних(англ. k-means), реализует, так называемую жесткую кластеризацию. Это значит, что вариант может принадлежать только одному кластеру. Идея алгоритма заключается в следующем [15]:
- Выбирается число кластеров k.
- Из исходного множества данных случайным образом выбираются k записей, которые будут служить начальными центрами кластеров.
- Для каждой записи исходной выборки определяется ближайший к ней центр кластера. При этом записи, "притянутые" определенным центром, образуют начальные кластеры.
- Вычисляются центроиды - центры тяжести кластеров. Каждый центроид - это вектор, элементы которого представляют собой средние значения признаков, вычисленные по всем записям кластера. Затем центр кластера смещается в его центроид.
Шаги 3 и 4 итеративно повторяются, при этом может происходить изменение границ кластеров и смещение их центров. В результате минимизируется расстояние между элементами внутри кластеров. Остановка алгоритма производится тогда, когда границы кластеров и расположения центроидов не перестанут изменяться от итерации к итерации, т.е. на каждой итерации в каждом кластере будет оставаться один и тот же набор записей.
Второй метод, реализованный в MicrosoftClustering, это максимизация ожиданий (англ. Expectation-maximization, EM). Он относится к методам мягкой кластеризации, т.е. вариант в этом случае принадлежит к нескольким кластерам и для всех возможных сочетаний вариантов с кластерами вычисляются вероятности.
При кластеризации методом EM [16] алгоритм итеративно уточняет начальную модель кластеризации, подгоняя ее к данным, и определяет вероятность принадлежности точки данных кластеру. Этот алгоритм заканчивает работу, когда вероятностная модель соответствует данным. Функция, используемая для установления соответствия, - логарифм функции правдоподобия данных, вводимых в модель.
Если в процессе формируются пустые кластеры или количество элементов в одном или нескольких кластерах оказывается меньше заданного минимального значения, малочисленные кластеры заполняются повторно с помощью новых точек и алгоритм EM запускается снова.Результаты метода масштабируемой максимизации ожидания являются вероятностными: каждая точка данных принадлежит всем кластерам, но с разной вероятностью. Поскольку метод допускает перекрытие кластеров, сумма элементов всех кластеров может превышать число элементов обучающего набора.
Реализация Майкрософт предоставляет два режима: масштабируемую и немасштабируемую максимизацию ожидания. По умолчанию при масштабируемой максимизации ожидания просматривается 50 000 записей. В случае успеха модель использует только эти данные. Если модель не удается подогнать на основании 50 000 записей, считываются еще 50 000 записей. При немасштабируемой максимизации ожидания считывается весь набор данных, независимо от его размера. Этот метод создает кластеры более точно, но предъявляет значительные требования к объему памяти.
По умолчанию используется масштабируемая максимизация ожидания, т.к. это более производительны алгоритм с меньшими требованиями к объему оперативной памяти.В большинстве случаев выигрыш в скорости не ведет к ухудшению качества окончательной модели.