Краткий обзор алгоритмов интеллектуального анализа данных. Упрощенный алгоритм Байеса. Деревья решений. Линейная регрессия
Упрощенный алгоритм Байеса (NaiveBayes)
Упрощенный алгоритм Байеса - это алгоритм классификации, основанный на вычислении условной вероятности значений прогнозируемых атрибутов. При этом и предполагается, что входные атрибуты являются независимыми и определен хотя бы один выходной атрибут.
Алгоритм основан на использовании формулы Байеса. Пусть  - полная группа несовместных событий, а
- полная группа несовместных событий, а  - некоторое событие, вероятность которого положительна. Тогда условная вероятность события
- некоторое событие, вероятность которого положительна. Тогда условная вероятность события  , если в результате эксперимента наблюдалось событие
, если в результате эксперимента наблюдалось событие  , может быть вычислена по формуле:
, может быть вычислена по формуле:
 |
( 9.1) |
В [1] работа алгоритма поясняется на следующем примере. В 2002 году в Конгрессе США был 51% представителей республиканской партии и 49% демократов. Имеется информация о том, как голосовали представители той и другой партии по ряду законопроектов (табл. 9.1). Пусть необходимо определить партийную принадлежность некоего конгрессмена. Без дополнительной информации мы можем сказать, что с вероятностью 0,49 он будет демократом, с вероятностью 0,51 - республиканцем. Это априорная ("заданная до опыта") вероятность, в формуле 9.1 обозначенная как  , где событие
, где событие  может заключаться в том, что данный депутат является демократом (Дем.) или республиканцем (Респ.).
может заключаться в том, что данный депутат является демократом (Дем.) или республиканцем (Респ.).
Но мы можем увеличить точность прогноза, если знаем, как голосовал данный депутат (табл. 9.2), и общие результаты голосования членов Конгресса по тем же вопросам (табл. 9.1).Формула Байеса позволяет вычислить условные (апостериорные, "полученные после опыта") вероятности.
| Зак-кт 1 | Зак-кт 2 | Зак-кт 3 | Зак-кт 4 | Партия | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Дем. | Респ. | Дем. | Респ. | Дем. | Респ. | Дем. | Респ. | Дем. | Респ. | |
| За | 41 | 214 | 87 | 211 | 184 | 172 | 178 | 210 | 211 | 223 |
| Против | 166 | 4 | 114 | 6 | 11 | 36 | 23 | 1 | ||
| За | 20% | 98% | 43% | 97% | 94% | 83% | 89% | 99.5% | 49% | 51% |
| Против | 80% | 2% | 57% | 3% | 6% | 17% | 11% | 0.5% | ||
| Зак-кт 1 | Зак-кт 2 | Зак-кт 3 | Зак-кт 4 | Партия |
|---|---|---|---|---|
| За | Против | За | За | ? |
Если известно, что каждый член конгресса должен принадлежать только одной из двух перечисленных партий, то полная группа событий - это {Дем.,Респ.}. Обозначим результаты голосования из табл. 9.2 как Рез. и воспользуемся правилом умножения вероятностей. Тогда условные вероятности можно рассчитать как:

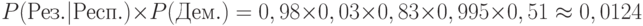


В итоге можно заключить, что с вероятностью около 0,79 рассматриваемый конгрессмен является представителем демократической партии.
Вернемся к теме интеллектуального анализа данных. Проводя аналогии, можно сказать, что таблица 9.1 - это результат обучения модели на исходных данных. В таблице 9.2 представлен классифицируемый вариант, а результат работы алгоритма - решение задачи классификации и оценка вероятности для предлагаемого варианта.
Если говорить о СУБД MS SQLServer 2008, то там описание модели интеллектуального анализа хранится в виде иерархии узлов. Для упрощенного алгоритма Байеса иерархия имеет 4 уровня. Среда разработки BIDevStudio позволяет просмотреть содержимое модели ( рис. 9.1). На верхнем уровне иерархии находится узел самой модели. Самый нижний уровень содержит информацию о том, с какой частотой встречались в обучающей выборке различные значения выходного параметра в сочетании с указанным значением выбранного входного параметра ( рис. 9.1).
увеличить изображение
Рис. 9.1. Просмотр модели на базе упрощенного алгоритма Байеса средствами BIDevStudio
Для корректного использования упрощенного алгоритма Байеса необходимо учитывать что:
- входные атрибуты должны быть взаимно независимыми;
- атрибуты могут быть только дискретными или дискретизированными (в процессе дискретизации множество значений непрерывного числового атрибута разбивается на интервалы и дальше идет работа с номером интервала);
- алгоритм требует меньшего количества вычислений, чем другие алгоритмы интеллектуального анализа, представляемые Microsoft SQLServer 2008, поэтому он часто используется для первоначального исследования данных. По той же причине, данный алгоритм предпочтителен для анализа больших наборов данных с большим числом входных атрибутов.
Деревья решений (DecisionTrees)
Деревья решений (или деревья принятия решений, англ. "DecisionTrees") - семейство алгоритмов, позволяющих сформировать правила классификации в виде иерархической (древовидной структуры). В ряде случаев, деревья решений позволяют также решать задачи регрессии и поиска взаимосвязей.
Решение задачи классификации заключается в определении значения категориального (дискретного) выходного атрибута на основании входных данных. Для этого сначала производится оценка степени корреляции входных и выходных значений, после чего обнаруженные зависимости описываются в виде узлов дерева.
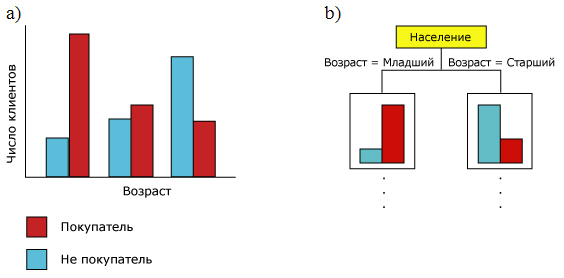
Рассмотрим следующий пример [6]. Пусть в обучающей выборке имеется информация о том, купил клиент велосипед или нет (прогнозируемое значение), а также о возрасте клиентов. На рис. 9.2a приведена гистограмма, показывающая зависимость прогнозируемогоатрибута "Покупатель велосипеда" от входного "Возраст" (будем считать, что возраст имеет три значения "Младший", "Средний", "Старший").Гистограмма 9.2b показывает, как эти данные могут использоваться при построении дерева решений.
По-другому алгоритм работает при построении дерева для прогнозирования непрерывного столбца [6]. В этом случае, каждый узел содержит регрессионную формулу, а разбиение осуществляется в точке нелинейности в этой формуле. Данный подход показан на рис. 9.3. Пусть наиболее точно имеющиеся данные можно моделировать двумя соединенными линиями ( рис. 9.3a). Дерево решений в этом случае строится так, как показано на рис. 9.3b).
В случае Microsoft SQLServer, для того, чтобы можно было получить функцию линейной регрессии, в набор стандартных алгоритмов, начиная с версии SQLServer 2005,был включен алгоритм линейной регрессии (MicrosoftLinearRegression) о котором речь пойдет ниже.
Но вернемся к деревьям решений. При решении задачи классификации, пройдя от корневого узла до конечного ("листа"), мы получаем результат.
Несомненным достоинством деревьев решений является их интуитивная понятность. В частности, описанные деревом зависимости можно легко перевести в правила "если-то". Например, попредставленному на рис. 9.4 фрагменту диаграммы можно составить правила следующего вида: "Если клиент владеет двумя машинами, проживает в регионе "Pacific" (Тихоокеанский) и моложе 43 лет, то он с высокой вероятностью приобретет велосипед".
При построении дерева решений важно добиться того, чтобы модель корректно отображала особенности предметной области и в то же время не содержала неоправданно большого числа ветвей. Слишком "ветвистое" дерево может отлично классифицировать данные из обучающего набора, но иметь невысокую точность прогнозирования для новых данных. Это явление называется "переобучением". Для борьбы с ним используется остановка при достижении определенных пороговых показателей (например, по объему данных, поддерживающих разбиение) и процедура "обрезки" дерева, в результате которой некоторые ветви объединяются или удаляются.
Линейная регрессия
Алгоритм линейной регрессии позволяетпредставить зависимость между зависимой и независимой переменными как линейную, а затем использовать полученный результат при прогнозировании.Подобный пример представлен на рис. 9.5. Линия на диаграмме является наилучшим линейным представлением данных.
В случае одной независимой переменной (одним регрессором) задача может быть сформулирована следующим образом. Уравнение описывающее линию:  . Для
. Для  -й точки будет справедливо
-й точки будет справедливо  , где
, где  - разница между фактическим значением
- разница между фактическим значением 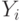 и вычисленным в соответствии уравнением линии. Иначе говоря, каждой точке соответствует ошибка, связанная с ее расстоянием от линии регрессии. Нужно с помощью подбора коэффициентов
и вычисленным в соответствии уравнением линии. Иначе говоря, каждой точке соответствует ошибка, связанная с ее расстоянием от линии регрессии. Нужно с помощью подбора коэффициентов  и
и  получать такое уравнение, чтобы сумма ошибок, связанных со всеми точками, стала минимальной. Для решения этой задачи может использоваться, в частности, метод наименьших квадратов.
получать такое уравнение, чтобы сумма ошибок, связанных со всеми точками, стала минимальной. Для решения этой задачи может использоваться, в частности, метод наименьших квадратов.
В SQLServer 2008 при выборе алгоритма линейной регрессии вызывается особый вариант алгоритма дерева решений с параметрами, которые ограничивают поведение алгоритма и требуют использования определенных типов данных на входе.
Линейная регрессия является полезным и широко известным методом моделирования, особенно для случаев, когда известен приводящий к изменениям базовый фактор и есть основания ожидать линейный характер зависимости. Существуют также и другие типы регрессии,в том числе - нелинейные.