Задачи, сгруппированные по методам решения. Все через площадь треугольника

Тест:

5,4
5
3,2
2,5
4,7
8,5
7,1

10,10
5
3,2
2,5
4,7
8,5
7,1

Задача 4: Определить, пересекаются ли два отрезка, заданные на плоскости координатами своих концов (примеры взаимного расположения отрезков на рис.10.5).

Рис. 10.5.

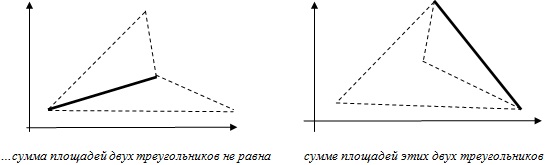
Идею решения задачи иллюстрирует схема (рис.10.6):

1. Отрезки пересекаются если:

   

   
   Рис. 10.6.

2. Отрезки не пересекаются (рис.10.7) если …

   

   
   Рис. 10.7.

Следует отметить, что данный метод определения пересечения двух отрезков имеет исключение, в случаях:

• если отрезки равной длины и параллельны;
• если отрезки находятся на одной прямой, но не имеют общих точек

Программа на Бейсике:

input "введите две координаты концов 1 отрезка"; x1,y1
input "введите две координаты концов 1 отрезка"; x2,y2
input "введите две координаты концов 2 отрезка"; xx1,yy1
input "введите две координаты концов 2 отрезка"; xx2,yy2
rem=площадь первой фигуры=======================
a=sqr ((xx1-xx2)^2+(yy1-yy2)^2)
b=sqr ((x1-xx1)^2+(y1-yy1)^2)
c=sqr ((x1-xx2)^2+(y1-yy2)^2)
p= (a+b+c)/2
s1=s1+sqr (p*(p-a)*(p-b)*(p-c))
rem
b=sqr ((x2-xx1)^2+(y2-yy1)^2)
c=sqr ((x2-xx2)^2+(y2-yy2)^2)
p= (a+b+c)/2
s1=s1+sqr (p*(p-a)*(p-b)*(p-c))
rem=площадь второй фигуры===========================
a=sqr ((x1-x2)^2+(y1-y2)^2)
b=sqr ((x2-xx1)^2+(y2-yy1)^2)
c=sqr ((x1-xx1)^2+(y1-yy1)^2)
p= (a+b+c)/2
s2=s2+sqr (p*(p-a)*(p-b)*(p-c))
rem
b=sqr ((x1-xx2)^2+(y1-yy2)^2)
c=sqr ((x2-xx2)^2+(y2-yy2)^2)
p= (a+b+c)/2
s2=s2+sqr (p*(p-a)*(p-b)*(p-c))
rem============================================
print s1,s2
if int(s1)=int(s2) then print  "пересекаются" else print "не пересекаются"

Программа на Паскале:

var x1,x2,y1,y2,xx1,xx2,yy1,yy2: integer;
  p,a,b,c,s1,s2:real;
begin
  writeln ('введите две координаты концов 1 отрезка');
  readln (x1,y1);
  writeln ('введите две координаты концов 1 отрезка');
  readln (x2,y2);
  writeln ('введите две координаты концов 2 отрезка');
  readln (xx1,yy1);
  writeln ('введите две координаты концов 2 отрезка');
  readln (xx2,yy2);
  {=====площадь первой фигуры=============}
  a:=sqrt (sqr(xx1-xx2)+sqr(yy1-yy2));
  b:=sqrt (sqr(x1-xx1)+sqr(y1-yy1));
  c:=sqrt (sqr(x1-xx2)+sqr(y1-yy2));
  p:= (a+b+c)/2;
  s1:=s1+sqrt (p*(p-a)*(p-b)*(p-c));
  {==================================}
  b:=sqrt (sqr(x2-xx1)+sqr(y2-yy1));
  c:=sqrt (sqr(x2-xx2)+sqr(y2-yy2));
  p:= (a+b+c)/2;
  s1:=s1+sqrt (p*(p-a)*(p-b)*(p-c));
  {=====площадь второй фигуры=============}
  a:=sqrt (sqr (x1-x2)+ sqr (y1-y2));
  b:=sqrt (sqr (x2-xx1)+ sqr (y2-yy1));
  c:=sqrt (sqr (x1-xx1)+ sqr (y1-yy1));
  p:= (a+b+c)/2;
  s2:=s2+sqrt (p*(p-a)*(p-b)*(p-c));
  {=================================}
  b:=sqrt (sqr (x1-xx2)+ sqr (y1-yy2));
  c:=sqrt (sqr (x2-xx2)+ sqr (y2-yy2));
  p:= (a+b+c)/2;
  s2:=s2+sqrt (p*(p-a)*(p-b)*(p-c));
  {==================================}
  writeln (s1,s2);
  if round(s1)=round(s2) then writeln ('пересекаются')
  else writeln ('не пересекаются');
end.

Тест:

2,4
8,7
3,8
8,1

3,6
8,1
6,5
11,7

Ключевые термины

• Формула Герона - формула для вычисления площади треугольника по длинам его сторон.

Краткие итоги

Для определения площади треугольника необходимо воспользоваться формулой Герона.

Для нахождения площади многоугольника потребуется найти сумму площадей треугольников, составляющих этот многоугольник.

Решение задач на определение вхождения точки в область многоугольника, пересечения двух отрезков необходимо также найти площади треугольников, составляющих фигуры.

Набор для практики

Вопросы.

• Какой формулой пользуются для вычисления площади треугольника?
• Каким способом вычисляют площадь многоугольника?
• Опишите метод для определения вхождения точки внутрь многоугольника.
• Подумайте, как можно определить "вхождение" одной фигуры в другую?
• Опишите метод для определения, пересекаются ли два отрезка.
• Подумайте - есть ли исключения у метода определения пересечения двух отрезков?

Упражнения.

• Треугольник на плоскости задан координатами своих вершин. Определить - прямоугольный ли этот треугольник?

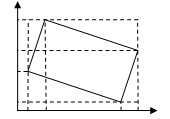
• Найти площадь 4-хугольника (не обязательно прямоугольника), заданного координатами своих вершин (на рис.10.8 изображен частный случай). Найти другой метод (кроме метода разбиения многоугольника на треугольники) нахождения площади этого прямоугольника.

  

  
  Рис. 10.8.
• С клавиатуры вводятся пары координат n точек на плоскости. Найти длину ломанной, соединяющей эти точки. Начало ломанной - ближайшая к центру координатной плоскости точка, ломанная соединяет все точки кратчайшим способом.
• Многоугольник задан координатами своих последовательных вершин. Внутренний угол в одной из вершин многоугольника - тупой. Определите эту вершину.