Типовые алгоритмы и задачи, решаемые с их помощью
Типовые алгоритмы обработки одномерных массивов
В данной теме будут рассматриваться такие типовые алгоритмы обработки одномерных массивов:
- Заполнение, вывод элементов массива
- Сумма, произведение элементов
- Выбор по условию
- Максимальный (минимальный) элемент
- Вставка, удаление элементов
- Инвертирование (изменения порядка следования элементов заданного массива на обратный)
Программные реализации типовых алгоритмов обработки одномерных массивов приведены в таблице 2.1:
| Типовой алгоритм | Программная реализация (Бейсик) | Программная реализация (Паскаль) |
|---|---|---|
| Заполнение массива |
input n dim a(n) for i=1 to n input a(i) next i |
const n=10; Var a: array [1..n] of integer; begin for i:=1 to n do readln (a[i]); … |
| Вывод в строку |
…for i=1 to n print a(i) ; " " ; next i |
… for i:=1 to n do write (a[i]); … |
| Сумма, произведение элементов |
… p=1 for i=1 to n s=s + a(i) p=p * a(i) next i |
… s:=0; p:=1; for i:=1 to n do begin s:=s+a[i]); p:=p*a[i]); end; … |
| Выбор по условию |
…
p = 1
for i = 1 to n
if {условие} then k=k+1:s=s+a(i):p=p*a(i)
next i
|
…
k:=0; s:=0; p:=1;
for i:=1 to n do
if {условие} then
begin
k:=k+1; s:=s+a[i]; p:=p*a[i];
end;
… |
| Максимальный (минимальный) элемент |
… max = a(1): min = a(1) for i = 2 to n if a(i) > max then max = a(i) if a(i) < min then min = a(i) next i |
… max:=a[1]; min:=a[1]; for i:=1 to n do begin if a[i] > max then max:=a[i]; if a[i] < min then min:=a[i]; end; |
| Вставка x на k-ое место |
dim a(n + 1) … for i = n to k step -1 a (i + 1) = a(i) next a(k) = x |
Var a: array [1..n+1] of… … for i:=n downto k do a[i+1]:=a[i]; a[k]:=x; … |
| Удаление k-ого элемента |
. . . for i = k to n - 1 a(i) = a(i + 1) next |
… for i:=k to (n-1) do a[i]:= a[i+1]; … |
| Инвертирование элементов |
. . . for i = 1 to n/2 swap a(i), a(n-i+1) next |
… for i:=1 to (n div 2) do begin х:=a[i]; a[i]:= a[n-i+1]; a[n-i+1] :=х; end … |
Ключевые моменты в типовых алгоритмах:
- Выбор по условию. В качестве условия может проверяться значение элемента массива на четность, кратность элемента какому-либо числу, положительность, отрицательность, равенство нулю. Может проверяться также и значение индекса элемента массива (например, элементы, стоящие на четных местах и др.).
-
Максимальный (минимальный) элемент. Кроме максимального элемента часто требуется найти и индекс максимального элемента:
if a[i]>max then begin max:=a[i]; imax:=i; end;
- Вставка x на k-ое место. Перестановка элементов (для освобождения "места" для вставляемого элемента) происходит с конца массива - последний элемент передвигается на "пустое место", на его место передвигается предпоследний элемент и т.д.
- Инвертирование элементов. Цикл работает n/2 раз, так как за один проход мы меняем сразу два элемента местами.
Задачи использованием типовых алгоритмов обработки одномерных массивов
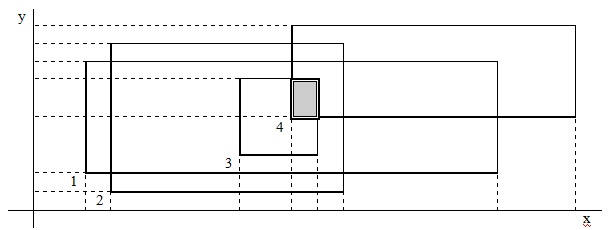
Задача: На плоскости изображено N прямоугольников (рис. 2.1). Каждый прямоугольник задан координатами левой нижней и правой верхней вершин. Определить, имеют ли прямоугольники общую площадь .
Идея решения:
Если:
- максимальная координата по оси Х левых нижних вершин прямоугольников будет меньше минимальной координаты правых верхних вершин и …
- …максимальная координата по оси У левых нижних вершин прямоугольников будет меньше минимальной координаты правых верхних вершин, то …
- …общая площадь есть.
В задаче необходимо использовать типовой алгоритм нахождения МАКСИМАЛЬНОГО (МИНИМАЛЬНОГО) ЭЛЕМЕНТА МАССИВА.
Для вычисления общей площади необходимо найти произведение разности:
- максимальной координаты по оси Х левых нижних вершин прямоугольников и минимальной координаты правых верхних вершин и …
- …максимальной координаты по оси У левых нижних вершин прямоугольников и минимальной координаты правых верхних вершин.
Программа на Бейсике:
input "введите количество прямоугольников"; n
dim x1(n), x2(n),y1(n), y2(n)
for i=1 to n
input x1(i), x2(i), y1(i), y2(i)
next
xmax=x1(1)
xmin=x2(1)
ymax=y1(1)
ymin=y2(2)
for i=1 to n
if x1(i) > xmax then xmax=x1(i)
if x2(i) < xmin then xmin=x2(i)
if y1(i) > ymax then ymax=y1(i)
if y2(i) < ymin then ymin=y2(i)
next
if xmax<xmin and ymax<ymin then print "общ. площадь есть" else print "общ. площади нет"
Программа на Паскале:
var x1, x2, y1, y2: array [1..10] of integer;
n, i, xmax, xmin, ymax, ymin: integer;
begin
writeln ('введите количество прямоугольников');
readln (n);
for i:=1 to n do
readln (x1[i], y1[i], x2[i], y2[i]);
xmax:=x1[1];
xmin:=x2[1];
ymax:=y1[1];
ymin:=y2[2];
for i:=1 to n do
begin
if x1[i] > xmax then xmax:=x1[i];
if x2[i] < xmin then xmin:=x2[i];
if y1[i] > ymax then ymax:=y1[i];
if y2[i] < ymin then ymin:=y2[i];
end;
if (xmax<xmin) and (ymax<ymin) then writeln ('общая площадь есть')
else writeln ('общей площади нет');
end.Тест:
| Дано: |
3 1,1,9,5 2,3,5,6 4,2,7,4 |
4 2,2,5,4 4,3,7,6 6,1,11,2 6,4,12,8 |
| Результат: | Общая площадь есть | Общей площади нет |
Задача: Латинским квадратом называется массив, в строках и столбцах которого нет одинаковых элементов. Вывести на экран латинский квадрат размером NxN.
Идея решения: Заполнить 1 строку квадратного массива (NxN) числами от 1 до N. Вторая строка массива получается путем циклического сдвига элементов первой строки и т. д. (табл. 2.2). Циклический сдвиг можно реализовать, используя типовой алгоритм ВСТАВКИ-УДАЛЕНИЯ (в зависимости от направления циклического сдвига).
| 1 | 2 | 3 | 4 | 5 |
| 5 | 1 | 2 | 3 | 4 |
| 4 | 5 | 1 | 2 | 3 |
| 3 | 4 | 5 | 1 | 2 |
| 2 | 3 | 4 | 5 | 1 |
Решение на Бейсике:
input "размерность="; n
dim a(n,n)
for j=1 to n
a(1,j)=j
next
rem=====сдвиг=========
for i=2 to n
for j=1 to n
a(i,j)=a(i-1,j)
next
x=a(i,n)
for j=n to 2 step -1
a(i,j)=a(i,j-1)
next
a(i,1)=x
next
rem====вывод==========
for i=1 to n
for j=1 to n
print a(i,j);
next
print
nextРешение на Паскале:
var a: array [1..10,1..10] of integer;
n,i,j,x: integer;
begin
writeln ('размерность=');
readln (n);
for j:=1 to n do a[1,j]:=j;
{======сдвиг======}
for i:=2 to n do
begin
for j:=1 to n do a[i,j]:=a[i-1,j];
x:=a[i,n];
for j:=n downto 2 do
a[i,j]:=a[i,j-1];
a[i,1]:=x;
end;
{======вывод======}
for i:=1 to n do
begin
for j:=1 to n do write(a[i,j]);
writeln;
end;
end.