Задачи, сгруппированные по методам решения. Все через площадь треугольника
Рассмотрим решение базовой задачи.
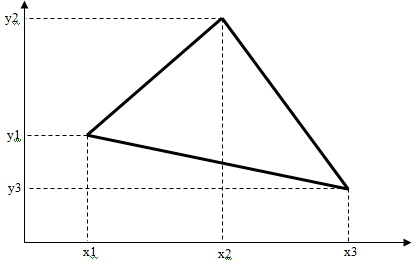
Задача : Найти площадь треугольника, заданного координатами своих вершин (рис.10.1).
Справочная информация: Для нахождения площади треугольника воспользуемся формулой Герона:
S=SQR (p(p-a)(p-b)(p-c))
где a, b, c - длины сторон, а р - полупериметр.
print "введите пары координат трех точек" input x1, y1 input x2, y2 input x3, y3 a= sqr ((x1-x2)^2+(y1-y2)^2) b= sqr ((x2-x3)^2+(y2-y3)^2) c= sqr ((x3-x1)^2+(y3-y1)^2) per= a+b+c print "периметр треугольника="; per p=per/2 s= sqr (p*(p-a)*(p-b)*(p-c)) print "площадь="; s
var x1,x2,x3,y1,y2,y3: integer;
a,b,c,p: real;
begin
writeln ('введите пары координат трех точек');
readln (x1, y1);
readln (x2, y2);
readln (x3, y3);
a:= sqrt (sqr(x1-x2)+sqr(y1-y2));
b:= sqrt (sqr(x2-x3)+sqr(y2-y3));
c:= sqrt (sqr(x3-x1)+sqr(y3-y1));
p:=(a+b+c) / 2;
writeln ('площадь треугольника:=', sqrt (p*(p-a)*(p-b)*(p-c)));
end.Тест:
Задача: Определить площадь выпуклой фигуры, заданной координатами своих вершин (координаты вводятся в соответствии с последовательным обходом вершин - см. рис.10.2).
Идея решения: задачу можно решить двумя способами.
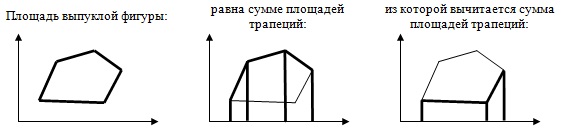
1 способ: площадь выпуклой фигуры равна сумме площадей треугольников, имеющих общую вершину:
input "введите количество вершин многоугольника"; n dim x(n), y(n) for i=1 to n input "введите пару координат"; x(i), y(i) next for i=2 to n-1 a= sqr ((x(1)-x(i))^2+(y(1)-y(i))^2) b= sqr ((x(i)-x(i+1))^2+(y(i)-y(i+1))^2) c= sqr ((x(i+1)-x(1))^2+(y(i+1)-y(1))^2) p= (a+b+c)/2 s=s+sqr (p*(p-a)*(p-b)*(p-c)) next print "площадь фигуры="; s
const nn=10 ;
var x,y: array [1..nn] of integer;
i, n: integer;
a, b, c, s, p: real;
begin
writeln ('введите количество вершин многоугольника');
readln (n);
for i:=1 to n do
begin
writeln (''введите пару координат');
readln (x[i], y[i]);
end;
for i:=2 to n-1 do
begin
a:= sqrt (sqr(x[1]-x[i])+sqr(y[1]-y[i]));
b:= sqrt (sqr(x[i]-x[i+1])+sqr(y[i]-y[i+1]));
c:= sqrt (sqr(x[i+1]-x[1])+sqr(y[i+1]-y[1]));
p:= (a+b+c)/2
s:=s+sqrt (p*(p-a)*(p-b)*(p-c))
end;
writeln ('площадь фигуры=', s);
end.Тест:
2 способ: Второй способ вычисления площади выпуклой фигуры иллюстрирует схема (рис. 10.3):
Решите задачу этим методом самостоятельно.
Задача 3: Определить - находится точка внутри или вне выпуклого многоугольника, заданного координатами своих вершин.
Идею решения задачи иллюстрирует схема (рис.10.4):
input "введите координаты точки"; x, y input "введите количество вершин многоугольника"; n dim x(n+1), y(n+1) for i=1 to n input "введите координаты вершин"; x(i), y(i) next x(n+1)=x(1) y(n+1)=y(1) rem====================================== for i=2 to n-1 a= sqr ((x(1)-x(i))^2+(y(1)-y(i))^2) b= sqr ((x(i)-x(i+1))^2+(y(i)-y(i+1))^2) c= sqr ((x(i+1)-x(1))^2+(y(i+1)-y(1))^2) p= (a+b+c)/2 s1=s1+sqr (p*(p-a)*(p-b)*(p-c)) next rem====================================== for i=1 to n a= sqr ((x-x(i))^2+(y-y(i))^2) b= sqr ((x(i)-x(i+1))^2+(y(i)-y(i+1))^2) c= sqr ((x(i+1)-x)^2+(y(i+1)-y)^2) p= (a+b+c)/2 s2=s2+sqr (p*(p-a)*(p-b)*(p-c)) next if s1=s2 then print "точка внутри" else print "точка вне фигуры"
const nn=100 ;
var x,y: array [1..nn] of integer;
i,xx,yy,n: integer;
a,b,c, p, s1,s2: real;
begin
writeln ('введите координаты точки');
readln (xx,yy);
writeln ('введите количество вершин многоугольника');
readln (n);
for i:=1 to n do
begin
writeln ('введите координаты вершин');
readln (x[i], y[i]);
end;
x[n+1]:=x[1];
y[n+1]:=y[1];
for i:=2 to n-1 do
begin
a:= sqrt (sqr(x[1]-x[i])+sqr(y[1]-y[i]));
b:= sqrt (sqr(x[i]-x[i+1])+sqr(y[i]-y[i+1]));
c:= sqrt (sqr(x[i+1]-x[1])+sqr(y[i+1]-y[1]));
p:= (a+b+c) / 2;
s1:=s1+sqrt (p*(p-a)*(p-b)*(p-c));
end;
for i:=1 to n do
begin
a:= sqrt (sqr(xx-x[i])+sqr(yy-y[i]));
b:= sqrt (sqr(x[i]-x[i+1])+sqr(y[i]-y[i+1]));
c:= sqrt (sqr(x[i+1]-xx)+sqr(y[i+1]-yy));
p:= (a+b+c) / 2;
s2:=s2+sqrt (p*(p-a)*(p-b)*(p-c));
end;
if round(s1)=round(s2) then writeln ('точка внутри')
else writeln ('точка вне фигуры');
end.