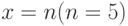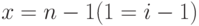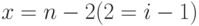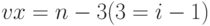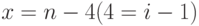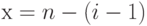Базовые формулы (зависимости) и задачи, решаемые с их помощью

Очень часто в решениях задач необходимо использовать ту или иную зависимость, применить формулу. Не стоит сейчас рассматривать большой круг математических формул, которые когда-либо использовались в решении задач по программированию (их достаточно много). А вот на некоторых из них, так называемых "базовых", стоит остановиться:

• Зависимость уменьшающейся переменной X в теле цикла от увеличивающегося значения счетчика цикла
• Признак кратности
• Нахождение длины отрезка по заданным координатам его концов.

Многие из рассмотренных ниже задач, опирающиеся на эти зависимости и формулы являются классическими в информатике.

Зависимость уменьшающейся переменной X в теле цикла от увеличивающегося значения счетчика цикла i

Для установления зависимости уменьшающейся переменной x в теле цикла от счетчика цикла, проанализируем значения переменных на каждом шаге выполнения тела цикла (проиллюстрированные в табл. 1.1):

Таблица 1.1.

1	5
2	4
3	3
4	2
5	1
Итого

Фрагменты программ, в котором реализована эта зависимость:

 …
for i=1 to n 
x=n-i+1 
next
…

…
for i:=1 to n do
x:=n-i+1;
…

Разбор задачи, приведенной ниже позволит закрепить полученные знания.

Задача "Палиндром": Определить, палиндром ли слово, введенное с клавиатуры (палиндром читается одинаково слева направо и справа налево).

Идея решения: Во введенной строке необходимо проверить - равны ли первый и последний символы, второй и предпоследний и т.д. (используя зависимость уменьшающейся переменной X в теле цикла от увеличивающегося значения счетчика цикла i).

Обратите внимание, что тело цикла выполняется n/2 раз (за один проход сравниваются 2 символа).

Программа на Бейсике:

input "введите слово"; a$
n=len (a$)
for i=1 to n/2
 if mid$ (a$,i,1)<> mid$ (a$,n-i+1,1) then k=1
next
if k=0 then print "палиндром" else print "не палиндром"

Программа на Паскале:

var a:string;
 k,n,i: integer;
begin
 writeln ('введите слово');
 readln (a);
 k:=0;
 n:=length(a);
 for i:=1 to (n div 2) do
  if copy(a,i,1) <> copy(a,n-i+1,1) then k:=1;
 if k=0 then writeln ('палиндром')
 else writeln ('не палиндром');
end.

Тест:

Длина отрезка

Для нахождения длины отрезка, заданного координатами своих концов (см. рис. 1.1) воспользуемся теоремой Пифагора:

Рис. 1.1.

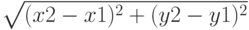
Арифметическое выражение для вычисления длины отрезка на Бейсике:

sqr ((x1-x2)^2+(y1-y2)^2)

Арифметическое выражения для вычисления длины отрезка на Паскале:

sqrt (sqr(x1-x2)+sqr(y1-y2))

Разбор решения задачи, приведенной ниже позволит закрепить полученные знания.

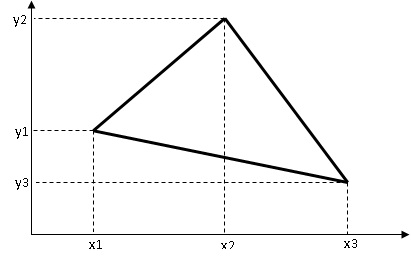
Задача: Найти периметр треугольника, координаты вершин которого вводятся с клавиатуры (рис. 1.2).

Рис. 1.2.

Идея решения: Для нахождения периметра треугольника необходимо найти длины его сторон.

Программа на Бейсике:

input x1, y1
input x2, y2
input x3, y3
ras1 = sqr((x1 - x2) ^ 2 + (y1 - y2) ^ 2)
ras2 = sqr((x2 - x3) ^ 2 + (y2 - y3) ^ 2)
ras3 = sqr((x1 - x3) ^ 2 + (y1 - y3) ^ 2)
print (ras1+ras2+ras3)

Программа на Паскале:

var   x1,y1,х2,y2,х3,у3: integer;
 ras1,ras2,ras3: real;
begin
 readln (x1, y1);
 readln (x2, y2);
 readln (x3, y3);
 ras1:=sqrt(sqr(x1-x2)+sqr(y1-y2)); 
 ras2:=sqrt(sqr(x2-x3)+sqr(y2-y3));
 ras3:=sqrt(sqr(x1-x3)+sqr(y1-y3));
 writeln (ras1+ras2+ras3);
end.

Тест:

Признак кратности числа Х числу У

Логические выражения для определения кратности числа Х числу У на Бейсике:

1. x \ y = x / y
2. x mod y =0

Логическое выражение для определения кратности числа Х числу У на Паскале:

x mod y = 0

Разбор решения задачи, приведенной ниже позволит закрепить полученные знания.

Задача: Найти делители введенного с клавиатуры числа N.

Идея решения: Во всех приведенных ниже задачах (набора для практики) необходимо воспользоваться формулой n mod i=0 (проверить - равен ли остаток от деления нулю). Cчетчик цикла "перебирает" возможные делители числа n.

Программа на Бейсике:

input "введите число"; n
print "делители:"
rem=вывод делителей========
for i=1 to n
 if n mod i=0 then print i; ",";
next

Программа на Паскале:

var n,i: integer;
begin
 writeln ('введите число');
 readln (n);
 writeln ('делители:');
 {=вывод делителей========}
for i:=1 to n do
  if n mod i=0 then write (i);
end.

Тест: