Задачи, сгруппированные по методам решения. От арифметического квадрата до кратчайшего пути (четыре задачи - один алгоритм)

Решение задачи на Бейсике:

input "введите степень", st
n=st+1
dim a (n,n)
for i=1 to n
  a(1,i)=1 
  a(i,1)=1
next
for i=2 to n
  for j=2 to n-i+1
    a(i,j)=a(i-1,j)+a(i,j-1)
next j,i
for i=1 to n
  print a(i,n-i+1); "*a^"; n-i; "*b^"; i-1; "+"; 
next i

Решение задачи на Паскале:

const m=10;
var a: array [1..m,1..m] of integer;
  st,n,i,j: integer;
begin
  writeln ('введите степень ');
  readln (st);
  n:=st+1;
  for i:=1 to n do
    begin
	a[1,i]:=1;
	a[j,1]:=1;
    end;
  for i:=2 to n do
    for j:=2 to (n-i+1) do
	  a[i,j]:=a[i-1,j]+a[i,j-1];
  for i:=1 to n do
	write (a[i,n-i+1], '*a^', n-i, '*b^', i-1, '+'); 
end.

Задача 4: Найти кратчайший путь в двумерном массиве из клетки 1,1 в клетку N, M. (путем называется набор индексов проходимых элементов, кратчайшим путем - набор индексов тех элементов массива, сумма значений которых минимальна). Двигаться можно только вниз либо вправо.

Идея решения:

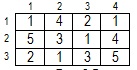
Допустим, дан массив (рис.8.5):

Рис. 8.5.

• Предположим, что мы будем двигаться от клетки (1,1) вправо по первой строке. Мы уже выяснили, что в каждую клетку первой строки ведет только один путь (см. "Арифметический квадрат"). Тогда пройденный к каждой клетке путь будет вычисляться как сумма значения данного элемента и элемента, стоящего левее (рис.8.6):

  

  
  Рис. 8.6.

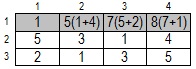
• Аналогично заполняем первый столбец (рис.8.7):

  

  
  Рис. 8.7.

• В клетку (2,2) можно попасть двумя путями - из клетки, стоящей выше или клетки, стоящей левее. Анализируем значения этих клеток (клетки, стоящей выше и клетки, стоящей левее). Из той клетки, значение которой меньше мы и придем в (2,2). Значит, значение клетки (2,2) увеличивается на 5 (рис.8.08):

  

  
  Рис. 8.08.
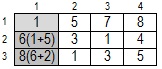
• Аналогично заполняем остальные элементы массива - сравниваем содержимое элемента, стоящего сверху и элемента cлева. То значение, которое меньше и прибавляем к содержимому текущего элемента.

• Вычисление координат: Движемся в обратном направлении: из клетки (n,m) к клетке (1,1). Анализируем содержимое элемента, стоящего левее и выше текущего. Координаты того элемента, значение которого меньше и выводим на экран (рис.8.09):

  

  
  Рис. 8.09.

Итого: Кратчайший путь - (3,4)-(3,3)-(2,3)-(1,3)-(1,2)-(1,1)

Решение задачи на Бейсике:

input "введите размерность массива", n, m
dim a(n,m)
for i=1 to n
  for j=1 to m
    input "введите элемент"; a(i,j)
  next j
next i
rem================================================
for j=2 to m
  a(1,j)= a(1,j)+ a(1,j-1)
next
for i=2 to n
  a(i,1)= a(i,1)+ a(i-1,1)
next
for i=2 to n
  for j=2 to m
	if a(i-1,j)<a(i,j-1) then a(i,j)=a(i,j)+a(i-1,j) else a(i,j)=a(i,j)+a(i,j-1)
  next j
next i
rem= вывод координат в обратном порядке======================
i=n
j=m
print  n,m
for x=1 to n+m-3
  if a(i-1,j)<a(i,j-1) then i=i-1 else j=j-1
  if i<>0 and j<>0 then print i;"-:;j
next 
print 1,1

Решение задачи на Паскале:

const nn=10;
mm=10;
var a: array [1..nn,1..mm] of integer;
  i,j,n,m,x: integer;
begin
  writeln ('введите размерность массива');
  readln (n, m);
  for i:=1 to n do
    for j:=1 to m do
	  readln (a[i,j]);
  for j:=2 to m do
     a [1,j]:= a [1,j]+ a [1,j-1];
  for i:=2 to n do
     a [i,1]:= a [i,1]+ a [i-1,1];
  for i:=2 to n do
	 for j:=2 to m do
	  if a [i-1,j]<a [i,j-1] then a [i,j]:=a [i,j]+a [i-1,j] 
	  else a [i,j]:=a [i,j]+a [i,j-1];
  i:=n;
  j:=m;
  {======вывод координат в обратном порядке======}
  writeln (n,m);
  for x:=1 to n+m-3 do
    begin
	 if a [i-1,j]<a [i,j-1] then i:=i-1 
	 else j:=j-1;
	 if (i<>0) and (j<>0) then writeln (i,j);
	 end;
  writeln (1,1);
end.

Ключевые термины

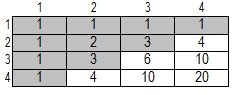
• Арифметический квадрат - двумерный массив, заполненный так: единичные элементы располагаются в первой строке и первом столбце. Остальные элементы заполняются суммой выше и левее стоящего элемента.
• Треугольник Паскаля - образован элементами, расположенными на и выше побочной диагонали арифметического квадрата.
• Бином Ньютона - формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных (формула разложения произвольной натуральной степени двучлена (а+b)ⁿ в многочлен).
• Путь в двумерном массиве - набор индексов проходимых элементов, кратчайшим путь - набор индексов тех элементов массива, сумма значений которых минимальна.

Краткие итоги

Способ заполнения Арифметического квадрата: единицами заполняются элементы первой строки и первого столбца. Остальные элементы заполняются суммой выше и левее стоящего элемента.

Элементы, расположенные на и выше побочной диагонали Арифметического квадрата образуют треугольник Паскаля.

На побочной диагонали Арифметического квадрата располагаются элементы, которые являются коэффициентами для слагаемых при разложении целой неотрицательной степени суммы двух переменных в Биноме Ньютона.

Нахождение кратчайшего пути в двумерном массиве также базируется на алгоритме создания Арифметического квадрата.

Набор для практики

Вопросы.

• Какое значение находится в элементе последней строки и последнего столбца Арифметического квадрата (какую информацию несет это число)?
• Пусть заполнение первой строки и первого столбца двумерного массива единицами идет в одном теле цикла. Каковы будут индексы элементов первой строки и индексы элементов первого столбца?
• Массив какой размерности необходимо заполнить, что бы получить коэффициенты для слагаемых при разложении суммы двух переменных в четвертой степени?

Упражнения.

• Вывести на экран Арифметический квадрат размерностью NxN (N ввести с клавиатуры).
• Вывести на экран коэффициенты для слагаемых при разложении суммы двух переменных в десятой степени.