Типовые алгоритмы обработки двумерных массивов
Типовые алгоритмы обработки двумерного массива относительно диагоналей
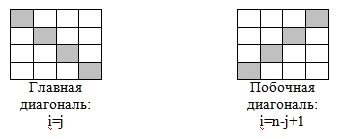
Если количество строк и столбцов в двумерном массиве одинаково, то такой массив называется квадратным. Типовые алгоритмы для квадратных массивов позволяют обрабатывать массив относительно его диагональных элементов. Зависимость индексов элементов, расположенных на побочной диагонали легко определяется при после повторения Лекции 1 (номер строки элемента растет, номер столбца убывает).
Главная диагональ. В таблице приведены типовые алгоритмы обработка элементов двумерного массива, расположенных НА, ВЫШЕ и НИЖЕ главной диагонали.
| Типовой алгоритм | Программная реализация (Бейсик) | Программная реализация (Паскаль) |
|---|---|---|
| Сумма элементов, расположенных НА главной диагонали |
… for i=1 to n s=s+x(i,i) next i … |
… s:=0; for i:=1 to n do s:=s+x[i,i]; … |
| Сумма элементов, расположенных ВЫШЕ главной диагонали |
… for i=1 to n for j=1 to n if i<j then s=s+x(i,j) next j, i … |
… s:=0; for i:=1 to n do for j:=1 to n do if i<j then s:=s+x[i,j]; … |
| Сумма элементов, расположенных НИЖЕ главной диагонали |
… for i=1 to n for j=1 to n if i>j then s=s+x(i,j) next j i … |
… s:=0; for i:=1 to n do for j:=1 to n do if i>j then s:=s+x[i,j]; … |
Побочная диагональ. В таблице приведены типовые алгоритмы обработка элементов двумерного массива, расположенных НА, ВЫШЕ и НИЖЕ побочной диагонали.
| Типовой алгоритм | Программная реализация (Бейсик) | Программная реализация (Паскаль) |
|---|---|---|
| Сумма элементов, расположенных НА побочной диагонали |
… for i=1 to n s=s+x(i, n-i+1) next i … |
… s:=0; for i:=1 to n do s:=s+x[i, n-i+1]; … |
| Сумма элементов, расположенных ВЫШЕ побочной диагонали |
… for i=1 to n for j=1 to n if (i<n-j+1) then s=s+x(i,j) next j, i … |
… s:=0; for i:=1 to n do for j:=1 to n do if (i<n-j+1) then s:=s+x[i,j]; … |
| Сумма элементов, расположенных НИЖЕ побочной диагонали |
… for i=1 to n for j=1 to n if (i>n-j+1) then s=s+x(i,j) next j, i … |
… s:=0; for i:=1 to n do for j:=1 to n do if (i>n-j+1) then s:=s+x[i,j]; … |
Обработка квадратной матрицы относительно диагоналей (рациональный обход)
Предложенные выше типовые алгоритмы обработки квадратного массива относительно диагоналей нерациональны, т.к. перебираются все элементы массива. Более рационально ограничить перебор элементов. Решит проблему введение зависимости начального или конечного значений управляющей переменной внутреннего цикла от значения счетчика внешнего цикла.
Рассмотрим типовые алгоритмы обработки квадратного массива относительно диагоналей рациональным способом на примерах.
Задача: заполнить элементы квадратного массива "1" так, как показано на рисунке:
| Ниже и на главной диагонали | Выше и на главной диагонали | Выше и на побочной диагонали | Ниже и на побочной диагонали |
|---|---|---|---|
|
100000000 110000000 111000000 111100000 111110000 111111000 111111100 111111110 111111111 |
111111111 011111111 001111111 000111111 000011111 000001111 000000111 000000011 000000001 |
111111111 111111110 111111100 111111000 111110000 111100000 111000000 110000000 100000000 |
000000001 000000011 000000111 000001111 000011111 000111111 001111111 011111111 111111111 |
|
Программная реализация на Бейсике: … for i=1 to n for j=1 to i x(i,j)=1 next j, i … Программная реализация на Паскале: … for i:=1 to n do for j:=1 to i do x[i,j]:=1; … |
Программная реализация на Бейсике: … for i=1 to n for j=i to n x(i,j)=1 next j, i … Программная реализация на Паскале: … for i:=1 to n do for j:=i to n do x[i,j]:=1; … |
Программная реализация на Бейсике: … for i=1 to n for j=1 to (n-i+1) x(i,j)=1 next j, i … Программная реализация на Паскале: … for i:=1 to n do for j:=1 to (n-i+1) do x[i,j]:=1; … |
Программная реализация на Бейсике: … for i=1 to n for j=(n-i+1) to n x(i,j)=1 next j, i … Программная реализация на Паскале: … for i:=1 to n do for j:=(n-i+1) to n do x[i,j]:=1; … |
Ключевые термины
- Двумерный массив -именованный набор однотипных переменных, расположенных в памяти непосредственно друг за другом, доступ к которым осуществляется по индексу. Массивы с одним индексом называют одномерными, с двумя - двумерными.
- Квадратный массив - двумерный массив, количество строк и столбцов в котором одинаково.
Краткие итоги
Для решения задач с использованием двумерных массивов необходимо воспользоваться типовыми алгоритмами обработки, такими как:
-
Обработка всего массива:
- Заполнение, вывод
- Сумма, произведение
- Максимальный (минимальный) элемент
- Выбор по условию
-
Обработка отдельно по строкам и столбцам:
- Заполнение, вывод
- Сумма, произведение
- Максимальный (минимальный) элемент
- Выбор по условию
-
Обработка относительно диагоналей:
- Заполнение, вывод
- Сумма, произведение
- Максимальный (минимальный) элемент
- Выбор по условию
При обработке квадратного массива относительно его диагоналей необходимо воспользоваться рациональным способом, исключающим обход всех элементов массива.
Набор для практики
Вопросы.
- Что произойдет если поменять местами счетчики внешнего и внутреннего цикла i и j в заголовках циклов (в типовом алгоритме обработки двумерного массива)?
- Какова зависимость индексов элементов, расположенных на главной диагонали квадратного массива? Побочной?
Упражнения.
- Найдите максимальный элемент из минимальных элементов каждой строки двумерного массива и минимальный элемент из максимальных элементов каждого столбца двумерного массива размерностью NxM.
- Заполните квадратные массивы, как предложено на рис. 5.2: