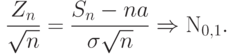Лекция 14: Характеристические функции
Доказательство ЗБЧ Хинчина
Пусть 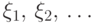 - последовательность
независимых в совокупности и одинаково распределенных случайных величин
с конечным первым моментом
- последовательность
независимых в совокупности и одинаково распределенных случайных величин
с конечным первым моментом  . Обозначим через
. Обозначим через  математическое ожидание
математическое ожидание 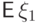 . Требуется доказать, что
. Требуется доказать, что
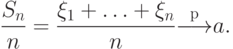
По свойству 26
сходимость по вероятности к постоянной эквивалентна
слабой сходимости.
Так как  - постоянная, достаточно доказать слабую сходимость
- постоянная, достаточно доказать слабую сходимость 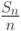 к
к  .
По теореме о непрерывном соответствии,
эта сходимость имеет место тогда и только тогда, когда для любого
.
По теореме о непрерывном соответствии,
эта сходимость имеет место тогда и только тогда, когда для любого 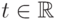 сходятся характеристические функции
сходятся характеристические функции

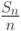 .
Пользуясь свойствами (Ф3) и (Ф4), получаем
.
Пользуясь свойствами (Ф3) и (Ф4), получаем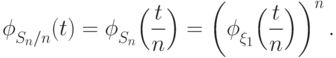
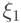 существует, поэтому свойство
(Ф6) позволяет
разложить
существует, поэтому свойство
(Ф6) позволяет
разложить 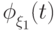 в ряд
Тейлора в окрестности нуля:
в ряд
Тейлора в окрестности нуля:
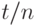 соответственно
соответственно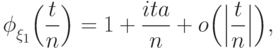

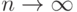 , пользуясь "замечательным пределом"
, пользуясь "замечательным пределом" 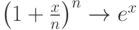 , получаем
, получаем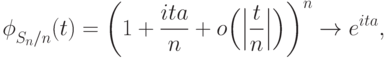
Доказательство центральной предельной теоремы
Пусть 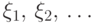 - последовательность
независимых в совокупности и одинаково распределенных случайных величин
с конечной и ненулевой дисперсией.
Обозначим через
- последовательность
независимых в совокупности и одинаково распределенных случайных величин
с конечной и ненулевой дисперсией.
Обозначим через  математическое ожидание
математическое ожидание 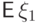 и через
и через  - дисперсию
- дисперсию 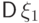 .
Требуется доказать, что
.
Требуется доказать, что

Введем "стандартизованные" случайные величины 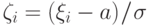 - независимые
случайные величины
с нулевыми математическими ожиданиями и единичными дисперсиями.
Пусть
- независимые
случайные величины
с нулевыми математическими ожиданиями и единичными дисперсиями.
Пусть 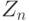 есть их сумма:
есть их сумма:
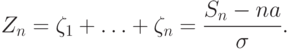
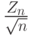 слабо сходится к стандартному нормальному
распределению.
Характеристическая функция величины
слабо сходится к стандартному нормальному
распределению.
Характеристическая функция величины 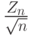 равна
равна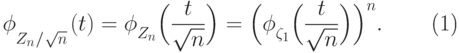 |
( 25) |
Характеристическую функцию случайной величины 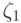 можно
разложить в ряд Тейлора,
в коэффициентах которого использовать известные моменты
можно
разложить в ряд Тейлора,
в коэффициентах которого использовать известные моменты 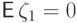 ,
, 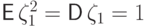 :
:
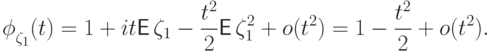
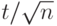 ,
в равенство (25)
и устремим
,
в равенство (25)
и устремим  к бесконечности. Еще раз воспользуемся замечательным
пределом:
к бесконечности. Еще раз воспользуемся замечательным
пределом: