Лекция 14: Характеристические функции
Пример 78.
Вычислим характеристическую функцию случайной величины  ,
имеющей нормальное распределение
с параметрами
,
имеющей нормальное распределение
с параметрами  и
и 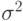 . Мы знаем, что у
"стандартизованной"
случайной величины,
. Мы знаем, что у
"стандартизованной"
случайной величины, 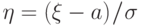 характеристическая функция
равна
характеристическая функция
равна  . Тогда характеристическая функция
величины
. Тогда характеристическая функция
величины  равна
равна
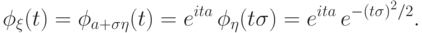
(Ф4). Характеристическая функция суммы
независимых случайных величин равна произведению характеристических
функций слагаемых: если случайные величины  и
и 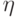 независимы, то, по свойству (E7)
математических ожиданий,
независимы, то, по свойству (E7)
математических ожиданий,

 случайных величин
распадалась в произведение их характеристических функций,
попарной независимости слагаемых не хватит.
То же самое можно сказать про свойство
(E7) математических ожиданий.
Если же сомножители независимы в совокупности, то их совместное
распределение распадается в произведение распределений, и тогда
математическое ожидание произведения распадается в произведение
математических ожиданий.
случайных величин
распадалась в произведение их характеристических функций,
попарной независимости слагаемых не хватит.
То же самое можно сказать про свойство
(E7) математических ожиданий.
Если же сомножители независимы в совокупности, то их совместное
распределение распадается в произведение распределений, и тогда
математическое ожидание произведения распадается в произведение
математических ожиданий.Замечательным свойством (Ф4) мы сразу же воспользуемся, как обещали, для доказательства леммы 3, утверждающей устойчивость нормального распределения относительно суммирования.
Доказательство леммы 3.
Пусть  и
и  независимы.
Характеристическая функция суммы
независимы.
Характеристическая функция суммы  равна
равна

 и
и  . Следовательно,
. Следовательно,  по свойству (Ф2).
по свойству (Ф2).Доказательство лемм 1, 2, 4. Докажем свойства устойчивости по суммированию биномиального распределения, распределения Пуассона и гамма-распределения, используя характеристические функции из примеров 73-76.
Для независимых случайных величин с распределениями Пуассона 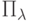 и
и  характеристическая функция
суммы
характеристическая функция
суммы
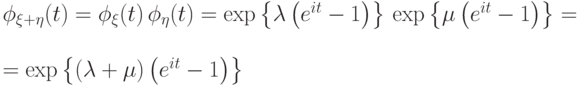
 .
.Для независимых случайных величин с биномиальными распределениями  и
и  характеристическая
функция суммы
характеристическая
функция суммы

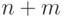 и
и  .
.Для независимых случайных величин с гамма-распределениями  и
и 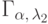 характеристическая функция
суммы
характеристическая функция
суммы

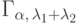 .
.(Ф5.) Пусть существует
момент порядка 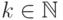 случайной величины
случайной величины  , т.е.
, т.е.  .
Тогда характеристическая функция
.
Тогда характеристическая функция 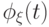 непрерывно
дифференцируема
непрерывно
дифференцируема  раз и ее
раз и ее  -я производная в
нуле
связана с моментом порядка
-я производная в
нуле
связана с моментом порядка  равенством
равенством

Существование и непрерывность  -й производной, равно как
и законность переноса производной под знак математического
ожидания, мы доказывать не будем.
-й производной, равно как
и законность переноса производной под знак математического
ожидания, мы доказывать не будем.
Упражнение.
Доказать, что для случайной величины  со стандартным
нормальным распределением
момент четного порядка
со стандартным
нормальным распределением
момент четного порядка 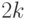 равен
равен
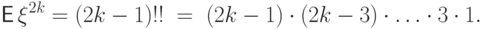
Как только появились производные высших порядков, самое время разложить функцию в ряд Тейлора.
(Ф6). Пусть существует
момент порядка  случайной величины
случайной величины  , т.е.
, т.е.  .
Тогда характеристическая функция
.
Тогда характеристическая функция 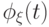 в окрестности точки
в окрестности точки  разлагается в ряд Тейлора
разлагается в ряд Тейлора
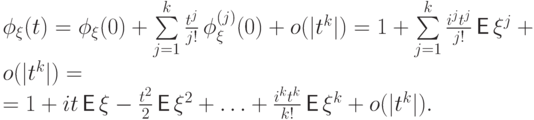
Ряды Тейлора бывают особенно полезны в теории пределов. Следующее основное свойство характеристических функций потребуется нам для доказательства предельных теорем, и это свойство - последняя теорема, оставленная нами без доказательства.
Теорема 43 (теорема Леви о непрерывном
соответствии).
Случайные величины 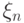 слабо сходятся к случайной величине
слабо сходятся к случайной величине  тогда и только тогда, когда для любого
тогда и только тогда, когда для любого  характеристические
функции
характеристические
функции 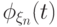 сходятся к характеристической функции
сходятся к характеристической функции 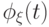 .
.
Сформулированная теорема устанавливает непрерывное соответствие
между классами 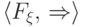 функций
распределения
со слабой сходимостью и
функций
распределения
со слабой сходимостью и  характеристических
функций со сходимостью в каждой точке. "Непрерывность" этого
соответствия
- в том, что пределу в одном классе относительно заданной в этом классе
сходимости соответствует предел в другом классе относительно сходимости,
заданной в этом другом классе.
характеристических
функций со сходимостью в каждой точке. "Непрерывность" этого
соответствия
- в том, что пределу в одном классе относительно заданной в этом классе
сходимости соответствует предел в другом классе относительно сходимости,
заданной в этом другом классе.
Осталось воспользоваться теоремой о непрерывном соответствии и доказать ЗБЧ в форме Хинчина и ЦПТ.
