НОУ ИНТУИТ | Введение в теорию вероятностей. Лекция 3: Аксиоматика теории вероятностей

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Новосибирский Государственный Университет

Опубликован: 07.04.2008 | Доступ: свободный | Студентов: 7243 / 1307 | Оценка: 4.56 / 4.32 | Длительность: 16:54:00

Тема: Математика

Специальности: Математик

Теги: алгебра, вычисления, графика, дискретное распределение, замечательный предел, коэффициент асимметрии, несовместное событие, полная группа, распределение бернулли, распределение коши, распределение пуассона, формула полной вероятности, функция Эйлера, цвета, элементы

|

Вам нравится? Нравится 73 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Алгебра событий. Сигма-алгебра событий. Свойства и примеры алгебр и сигма-алгебр. Мера и ее свойства. Вероятность как нормированная мера. Свойства вероятности. Примеры

Алгебра и сигма-алгебра событий

Алгебра событий. Пусть $\Omega$ - пространство элементарных исходов некоторого случайного эксперимента (т.е. непустое множество произвольной природы). Мы собираемся определить набор подмножеств $\Omega$ , которые будут называться событиями, и затем задать вероятность как функцию, определенную только на множестве событий.

Итак, событиями мы будем называть не любые подмножества $\Omega$ , а лишь элементы некоторого выделенного набора подмножеств множества $\Omega$ . При этом необходимо позаботиться, чтобы этот набор подмножеств был замкнут относительно обычных операций над событиями, т.е. чтобы объединение, пересечение, дополнение событий снова давало событие. Сначала введем понятие алгебры множеств.

Определение 4 Множество 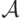$\mathcal A$ , элементами которого являются подмножества множества $\Omega$ (не обязательно все) называется алгеброй, если оно удовлетворяет следующим условиям:

(A1) 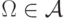$\Omega\in \mathcal A$ (алгебра содержит достоверное событие);

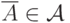(A2) если $A\in\mathcal A$ , то $\overline A\in\mathcal A$ (вместе с любым множеством алгебра содержит противоположное к нему);

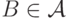(A3) если $A\in\mathcal A$ и $B \in\mathcal A$ , то $A\cup B\in\mathcal A$ (вместе с любыми двумя множествами алгебра содержит их объединение).

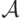Из (A1) и (A2) следует, что пустое множество $\emptyset=\overline{\Omega}$ также содержится в $\mathcal A$ , т.е. алгебра содержит и невозможное событие.

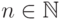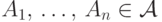Из условия (A3) следует, что вместе с любым конечным набором множеств алгебра содержит их объединение: для любого $n\in\mathbb N$ , для любых $A_1,\,\dots,\,A_n\in\mathcal A$ выполнено $A_1\cup\ldots\cup A_n \in\mathcal A$ .

Вместо замкнутости относительно объединения можно требовать замкнутость относительно пересечения.

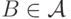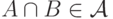Свойство 1. В определении 4 можно заменить (А3) на (А4) если $A\in\mathcal A$ и $B\in\mathcal A$ , то $A\cap B\in\mathcal A$ .

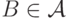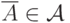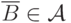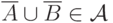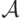Доказательство. Докажем, что при выполнении (A1) и (A2) из (A3) следует (A4). Если , $B\in\mathcal A$ , то $\overline A\in\mathcal A$ и $\overline B\in \mathcal A$ по свойству (A2). Тогда из (A3) следует, что $\overline A\cup\overline B\in\mathcal A$ . Вновь пользуясь (A2), получим, что дополнение $\overline{\overline A\cup\overline B}$ к этому множеству также принадлежит алгебре $\mathcal A$ . В силу формул двойственности, дополнение к объединению равно пересечению дополнений:

$A\cap B= \overline{\overline A\cup\overline B}\in\mathcal A.$

Аналогично доказывается, что при выполнении (A1) и (A2) из (A4) следует (A3), т.е. эти два свойства в определении взаимозаменяемы.

Пример 22. Пусть $\Omega=\{\spadesuit,\, \clubsuit,\,\diamondsuit,\,\heartsuit\}$ - пространство элементарных исходов. Следующие наборы подмножеств $\Omega$ являются алгебрами:

$\mathcal A = \{\Omega, \emptyset\}= \{\{ \spadesuit,\,\clubsuit,\,\diamondsuit,\,\heartsuit\}, \emptyset \}$ - тривиальная алгебра;
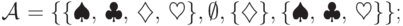
$\mathcal A\mspace{1mu} = \{\{ \spadesuit,\,\clubsuit,\,\diamondsuit,\,\heartsuit\}, \emptyset, \{\diamondsuit\}, \{\spadesuit,\,\clubsuit,\,\heartsuit\} \};$
$\mathcal A=2^\Omega$ - множество всех подмножеств $\Omega$ .

Упражнение. Доказать, что если $\Omega$ состоит из элементов, то в множестве всех его подмножеств ровно 2^n элементов.

Сигма-алгебра событий. В теории вероятностей часто возникает необходимость объединять счетные наборы событий и считать событием результат такого объединения. При этом свойства (A3) алгебры оказывается недостаточно: из него не вытекает, что объединение счетной последовательности множеств из алгебры снова принадлежит алгебре. Поэтому разумно наложить более суровые ограничения на класс событий.

Определение 5. Множество 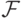$\mathcal F$ , элементами которого являются подмножества множества $\Omega$ (не обязательно все) называется $\sigma$ -алгеброй ( $\sigma$ -алгеброй событий), если выполнены следующие условия:

(S1) 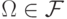$\Omega\in \mathcal F$ ( $\sigma$ -алгебра событий содержит достоверное событие);

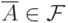(S2) если $\vphantom{\int^1}A\in\mathcal F$ , то $\overline A\in\mathcal F$ (вместе с любым событием $\sigma$ -алгебра содержит противоположное событие);

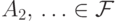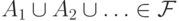(S3) если A_1 , $A_2,\, \ldots\in\mathcal F$ , то $A_1\cup A_2\cup\ldots\in\mathcal F$ (вместе с любым счетным набором событий $\sigma$ -алгебра содержит их объединение).

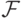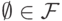Упражнение. Доказать, что вместо (S1) достаточно предположить непустоту множества $\mathcal F$ . Вывести из (S1) и (S2), что $\emptyset\in\mathcal F$ .

Этого набора аксиом достаточно для замкнутости множества 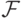$\mathcal F$ относительно счетного числа любых других операций над событиями. В частности, аналогично свойству 1 проверяется следующее утверждение.

Свойство 2. В определении 5 можно заменить (S3) на (S4): (S4) если 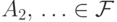A_1 , $A_2,\, \ldots\in\mathcal F$ , то $A_1\cap A_2\cap\ldots\in\mathcal F$ .

Дальше >>

Авторизоваться

Введение в теорию вероятностей

Аксиоматика теории вероятностей

Алгебра и сигма-алгебра событий

Вопросы и ответы