Лекция 12: Сходимость последовательностей случайных величин
Законы больших чисел
Определение 45.
Говорят, что последовательность случайных величин 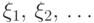 с конечными первыми моментами удовлетворяет закону больших чисел
(ЗБЧ), если
с конечными первыми моментами удовлетворяет закону больших чисел
(ЗБЧ), если
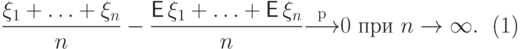 |
( 20) |
Законами больших чисел принято называть утверждения о том, при каких условиях последовательность случайных величин удовлетворяет закону больших чисел.
Выясним сначала, когда выполнен ЗБЧ для последовательности независимых и одинаково распределенных случайных величин.
Теорема 36 (ЗБЧ Чебышёва).
Для любой последовательности 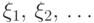 попарно
независимых и одинаково
распределенных случайных величин с конечным вторым моментом
попарно
независимых и одинаково
распределенных случайных величин с конечным вторым моментом  имеет место сходимость
имеет место сходимость
 |
( 21) |
Заметим, что если величины одинаково распределены, то их математические
ожидания
одинаковы (и равны, например, 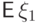 ),
поэтому свойство (20) можно записать в
виде (21).
),
поэтому свойство (20) можно записать в
виде (21).
ЗБЧ утверждает, что среднее арифметическое большого числа случайных слагаемых "стабилизируется" с ростом этого числа. Как бы сильно каждая случайная величина ни отклонялась от своего среднего значения, при суммировании эти отклонения "взаимно гасятся", так что среднее арифметическое приближается к постоянной величине.
В дальнейшем мы увидим, что требование конечности второго момента (или дисперсии) связано исключительно со способом доказательства, и что утверждение останется верным, если требовать существования только первого момента.
Доказательство.
Обозначим через  сумму первых
сумму первых  случайных
величин.
Из линейности математического ожидания получим
случайных
величин.
Из линейности математического ожидания получим
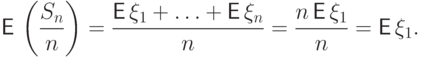
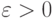 .
Воспользуемся неравенством Чебышёва (следствие 17):
.
Воспользуемся неравенством Чебышёва (следствие 17):![\[
\mathsf P\left(\left|\dfrac{S_n}{n}
- \mathsf E \left(\dfrac{S_n}{n}\right)\right|\ge \varepsilon\right)
\le \dfrac{\mathsf D \left(\dfrac{S_n}{n}\right)}{\varepsilon^2}=
\dfrac{\mathsf D S_n}{n^2\varepsilon^2} =
\dfrac{\mathsf D \xi_1+\ldots+\mathsf D \xi_n}{n^2\varepsilon^2}
= \dfrac{n\, \mathsf D \xi_1}{n^2\varepsilon^2} =
\dfrac{\mathsf D \xi_1}{n \varepsilon^2} \to 0
\]
при $n\to\infty$,](/sites/default/files/tex_cache/ee6f5ebda8e101b7a75c907182fbcc45.png)
 . Дисперсия суммы превратилась в сумму дисперсий в силу попарной
независимости слагаемых, из-за которой все ковариации
. Дисперсия суммы превратилась в сумму дисперсий в силу попарной
независимости слагаемых, из-за которой все ковариации  в свойстве 19) обратились в нуль при
в свойстве 19) обратились в нуль при 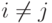 .
.Замечание.
Мы не только доказали сходимость, но и
получили оценку для вероятности среднему арифметическому
любого числа попарно независимых и одинаково распределенных величин
отличаться от 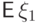 более чем на
заданное
более чем на
заданное 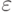 :
:
 |
( 23) |
Попарную независимость слагаемых в ЗБЧ Чебышёва можно заменить их попарной некоррелированностью, ничего не меняя в доказательстве. ЗБЧ может выполняться и для последовательности зависимых и разнораспределенных слагаемых. Из неравенства Чебышёва сразу вытекает следующее достаточное условие выполнения ЗБЧ для последовательности произвольных случайных величин.
Теорема 37 (ЗБЧ Маркова).
Последовательность случайных величин 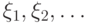 с конечными вторыми моментами удовлетворяет ЗБЧ, если
с конечными вторыми моментами удовлетворяет ЗБЧ, если  , т.е. если
, т.е. если  при
при 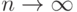 .
.
Теорема Маркова утверждает, что ЗБЧ выполнен, если дисперсия суммы  слагаемых растет не слишком быстро с ростом
слагаемых растет не слишком быстро с ростом  .
.
Сильная зависимость слагаемых приводит обычно
к невыполнению ЗБЧ. Если, например, 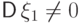 и
и  , то
, то  , и свойство (21)
не выполнено.
В этом случае не выполнено и достаточное условие для ЗБЧ:
, и свойство (21)
не выполнено.
В этом случае не выполнено и достаточное условие для ЗБЧ:  .
Для одинаково распределенных слагаемых дисперсия суммы еще быстрее расти уже
не может.
.
Для одинаково распределенных слагаемых дисперсия суммы еще быстрее расти уже
не может.
Следующее утверждение мы докажем чуть позже. Сравните его условия с условиями ЗБЧ Чебышёва.
Теорема 38 (ЗБЧ Хинчина).
Для любой последовательности 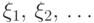 независимых в совокупности
и одинаково распределенных случайных величин с конечным первым моментом
независимых в совокупности
и одинаково распределенных случайных величин с конечным первым моментом  имеет место сходимость:
имеет место сходимость:

Итак, чтобы последовательность независимых и одинаково
распределенных случайных величин удовлетворяла ЗБЧ, достаточно
существования первого момента слагаемых.
Более того, в условиях теоремы 38
имеет место
и сходимость п.н. последовательности  к
к 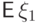 .
Это утверждение
называется усиленным законом больших чисел (УЗБЧ) Колмогорова,
и его мы доказывать не будем.
.
Это утверждение
называется усиленным законом больших чисел (УЗБЧ) Колмогорова,
и его мы доказывать не будем.
Получим в качестве следствия из ЗБЧ Чебышёва закон больших чисел Бернулли. В отличие от ЗБЧ Чебышёва, описывающего предельное поведение среднего арифметического случайных величин с произвольными распределениями, ЗБЧ Бернулли - утверждение только для схемы Бернулли.
Теорема 39 (ЗБЧ Бернулли).
Пусть событие  может произойти
в любом из
может произойти
в любом из  независимых испытаний с одной и той же вероятностью
независимых испытаний с одной и той же вероятностью  , и пусть
, и пусть 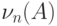 - число осуществлений события
- число осуществлений события  в
в  испытаниях. Тогда
испытаниях. Тогда 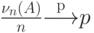 .
При этом для любого
.
При этом для любого 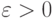
Доказательство.
Заметим, что 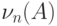 есть сумма независимых,
одинаково распределенных случайных величин, имеющих распределение Бернулли
с параметром
есть сумма независимых,
одинаково распределенных случайных величин, имеющих распределение Бернулли
с параметром 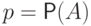 (индикаторов того, что в соответствующем испытании произошло
(индикаторов того, что в соответствующем испытании произошло  ):
):  , где
, где

 ,
, 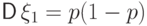 .
Осталось воспользоваться ЗБЧ в форме Чебышёва и неравенством
(23).
.
Осталось воспользоваться ЗБЧ в форме Чебышёва и неравенством
(23).Пример 71.
Монета подбрасывается  раз. Оценим вероятность того, что
частота выпадения герба отличается от
раз. Оценим вероятность того, что
частота выпадения герба отличается от  на
на 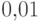 или более.
или более.
Пусть  - независимые случайные величины,
каждая из которых имеет
распределение Бернулли с параметром
- независимые случайные величины,
каждая из которых имеет
распределение Бернулли с параметром 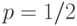 и равна
единице, если при соответствующем подбрасывании выпал герб, и нулю иначе.
Нужно оценить
и равна
единице, если при соответствующем подбрасывании выпал герб, и нулю иначе.
Нужно оценить  ,
где
,
где 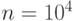 , а
, а  -
число выпадений герба.
Поскольку
-
число выпадений герба.
Поскольку 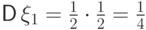 , искомая
оценка сверху
выглядит так:
, искомая
оценка сверху
выглядит так:

Итак, неравенство Чебышёва позволяет заключить,
что в среднем не более чем в четверти случаев при 10 000 подбрасываниях
монеты частота выпадения герба будет отличаться
от  на одну сотую или больше.
Мы увидим, насколько это грубая оценка, когда познакомимся с
центральной предельной теоремой.
на одну сотую или больше.
Мы увидим, насколько это грубая оценка, когда познакомимся с
центральной предельной теоремой.
