Преобразования случайных величин
Примеры использования формулы свертки
Пример 45.
Пусть независимые случайные величины  и
и 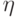 имеют стандартное
нормальное распределение. Докажем, что их сумма имеет нормальное распределение
с параметрами
имеют стандартное
нормальное распределение. Докажем, что их сумма имеет нормальное распределение
с параметрами 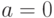 и
и 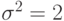 .
.
Доказательство. По формуле свертки, плотность суммы равна
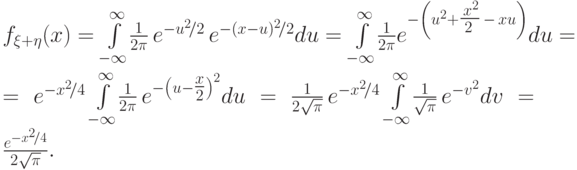
Последний интеграл равен единице, поскольку под интегралом стоит плотность
нормального распределения с параметрами 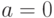 и
и 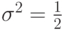 .
Итак, мы получили, что плотность распределения
суммы есть плотность нормального
распределения с параметрами
.
Итак, мы получили, что плотность распределения
суммы есть плотность нормального
распределения с параметрами  и
и 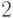 .
.
Если сумма двух независимых случайных величин из одного и того же распределения (возможно, с разными параметрами) имеет такое же распределение, говорят, что это распределение устойчиво относительно суммирования. В следующих утверждениях перечислены практически все устойчивые распределения.
Лемма 1.
Пусть случайные величины 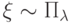 и
и 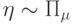 независимы. Тогда
независимы. Тогда 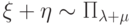 .
.
Доказательство. Найдем таблицу распределения суммы. Для любого целого 
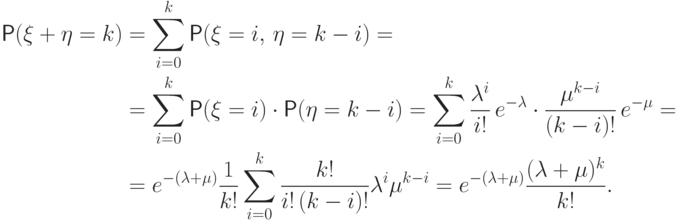
Лемма 2.
Пусть случайные величины 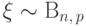 и
и 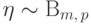 независимы.
Тогда
независимы.
Тогда 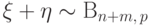 .
.
Смысл леммы 2 совершенно
понятен: складывая количество успехов в
первых  и в следующих
и в следующих  независимых испытаниях
одной и той же
схемы Бернулли, получаем количество успехов в
независимых испытаниях
одной и той же
схемы Бернулли, получаем количество успехов в 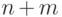 испытаниях. Полезно
доказать это утверждение аналогично тому, как мы доказали лемму 1.
испытаниях. Полезно
доказать это утверждение аналогично тому, как мы доказали лемму 1.
Лемма 3.
Пусть случайные величины  и
и  независимы.
Тогда
независимы.
Тогда  .
.
Лемма 4.
Пусть случайные величины  и
и 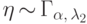 независимы.
Тогда
независимы.
Тогда 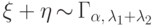 .
.
Эти утверждения мы докажем позднее, используя аппарат характеристических функций, хотя при некотором терпении можно попробовать доказать их напрямую с помощью формулы свертки.
Показательное распределение не устойчиво по суммированию, однако оно является частным случаем гамма-распределения, которое уже устойчиво относительно суммирования. Докажем частный случай леммы 4.
Лемма 5.
Пусть независимые случайные величины  имеют показательное распределение
имеют показательное распределение 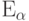 .
Тогда
.
Тогда  .
.
Доказательство.
Докажем утверждение по индукции. При 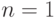 оно верно в силу
равенства
оно верно в силу
равенства 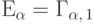 .
Пусть утверждение леммы справедливо для
.
Пусть утверждение леммы справедливо для 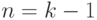 . Докажем, что оно
верно
и для
. Докажем, что оно
верно
и для 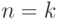 . По предположению индукции,
. По предположению индукции,  имеет распределение
имеет распределение 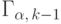 ,
т.е. плотность распределения величины
,
т.е. плотность распределения величины 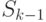 равна
равна

 равна
равна
 при
при 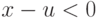 , т.е. при
, т.е. при  ,
то плотность под интегралом отлична от нуля, только если переменная
интегрирования изменяется в пределах
,
то плотность под интегралом отлична от нуля, только если переменная
интегрирования изменяется в пределах 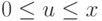 при
при  .
При
.
При  подынтегральная функция равна нулю. При
подынтегральная функция равна нулю. При  имеем
имеем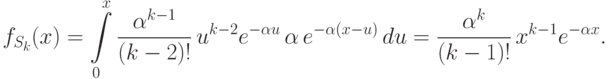
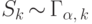 , что и требовалось доказать.
, что и требовалось доказать.Пример 46.
Равномерное распределение не является устойчивым относительно суммирования.
Найдем функцию и плотность распределения суммы двух независимых случайных
величин с одинаковым равномерным на отрезке ![[0,\,1]](/sites/default/files/tex_cache/3c677f273d5640cb290c4e4ac717fbc7.png) распределением, но не
по формуле свертки, а используя геометрическую вероятность.
распределением, но не
по формуле свертки, а используя геометрическую вероятность.
Пусть 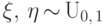 - независимые
случайные величины.
Случайные величины
- независимые
случайные величины.
Случайные величины  и
и 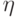 можно считать
координатами точки, брошенной
наудачу в единичный квадрат.
можно считать
координатами точки, брошенной
наудачу в единичный квадрат.
Тогда 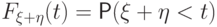 равна площади
области внутри квадрата под прямой
равна площади
области внутри квадрата под прямой 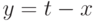 . Эта область
- заштрихованный на
рис.
9.1
треугольник (при
. Эта область
- заштрихованный на
рис.
9.1
треугольник (при 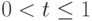 )
либо пятиугольник (при
)
либо пятиугольник (при 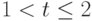 ).
Получим функцию распределения и плотность распределения суммы двух независимых
равномерно распределенных на отрезке
).
Получим функцию распределения и плотность распределения суммы двух независимых
равномерно распределенных на отрезке ![[0,\,1]](/sites/default/files/tex_cache/3c677f273d5640cb290c4e4ac717fbc7.png) случайных величин:
случайных величин:
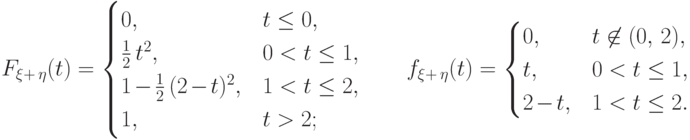
Полученное распределение называется "треугольным распределением" Симпсона. Видим, что распределение суммы независимых случайных величин с равномерным распределением не является равномерным.
Пример 47.
Найдем функцию и плотность распределения частного двух независимых случайных
величин  и
и 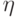 , имеющих показательное
распределение с параметром
, имеющих показательное
распределение с параметром  .
.

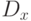 есть множество точек
есть множество точек 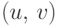 таких,
что
таких,
что 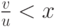 . При этом достаточно ограничиться положительными
значениями
. При этом достаточно ограничиться положительными
значениями  и
и 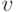 : показательно распределенные
случайные величины
могут принимать отрицательные значения лишь с нулевой вероятностью.
: показательно распределенные
случайные величины
могут принимать отрицательные значения лишь с нулевой вероятностью.Вычислим интеграл по области 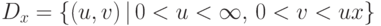 :
:
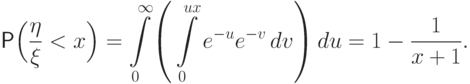
Упражнение.Провести вычисления и получить ответ. Таким образом, функция и плотность распределения частного имеют вид