Элементарная теория вероятностей
Пример 14.
Рассмотрим выбор двух шариков из двух или, что то же самое,
дважды подбросим монету.
Если учитывать порядок, то исходов получится четыре, и они равновозможны,
т.е. имеют вероятности по 


 а вероятность
последнего
равна
а вероятность
последнего
равна  Видим, что
при выборе с возвращением и без учета порядка элементарные исходы
оказываются неравновозможными.
Видим, что
при выборе с возвращением и без учета порядка элементарные исходы
оказываются неравновозможными.Упражнение.
Сравнить примеры 2 и 3. В каком из них
перечислены равновозможные элементарные исходы? Найти вероятности
всех элементарных исходов в примере 3. Равны ли они  . Равны ли
они?
. Равны ли
они?
В следующем примере разобрана классическая задача, приводящая к так называемому гипергеометрическому распределению.
Пример 15.
Из урны, в которой 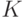 белых и
белых и  черных шаров,
наудачу и без возвращения вынимают
черных шаров,
наудачу и без возвращения вынимают  шаров, где
шаров, где  (
рис.
2.1).
Термин "наудачу" означает, что появление любого набора
из
(
рис.
2.1).
Термин "наудачу" означает, что появление любого набора
из  шаров равновозможно. Найти вероятность того, что
будет выбрано
шаров равновозможно. Найти вероятность того, что
будет выбрано  белых и
белых и 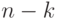 черных шаров.
черных шаров.
Решение.
Результат эксперимента - набор из  шаров. Можно не учитывать
порядок следования шаров в наборе. Общее число элементарных исходов по
теореме 3
равно
шаров. Можно не учитывать
порядок следования шаров в наборе. Общее число элементарных исходов по
теореме 3
равно 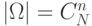 . Обозначим
через
. Обозначим
через  событие, состоящее в том, что в наборе
окажется
событие, состоящее в том, что в наборе
окажется  белых шаров и
белых шаров и 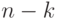 черных. Пусть
черных. Пусть 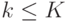 и
и 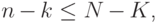 иначе
иначе 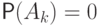 . Есть ровно
. Есть ровно 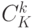 способов
выбрать
способов
выбрать  белых шаров
из
белых шаров
из 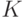 и
и  способов
выбрать
способов
выбрать 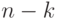 черных шаров из
черных шаров из  Каждый
возможный набор выбранных белых шаров можно комбинировать
с каждым возможным набором черных. По теореме о перемножении шансов
число благоприятных
исходов равно
Каждый
возможный набор выбранных белых шаров можно комбинировать
с каждым возможным набором черных. По теореме о перемножении шансов
число благоприятных
исходов равно  , и
вероятность события
, и
вероятность события  такова:
такова:
 |
( 2.2) |
Вычисляя вероятность событий  мы сопоставили каждому
набору
из
мы сопоставили каждому
набору
из  белых и
белых и 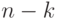 черных шаров вероятность получить этот
набор при выборе
шаров из урны. Набор вероятностей (2.2)
называется гипергеометрическим распределением вероятностей.
черных шаров вероятность получить этот
набор при выборе
шаров из урны. Набор вероятностей (2.2)
называется гипергеометрическим распределением вероятностей.
Здесь мы в первый, но далеко не в последний раз встретились с термином "распределение" вероятностей. Это слово всегда обозначает некий способ разделить (распределить) общую единичную вероятность между какими-то точками или множествами {на вещественной прямой}.
Пример 16. На пяти карточках написаны буквы А, А, Л, М, П. Найти вероятность того, что при случайной расстановке этих карточек в ряд получится слово ЛАМПА.
Решение.
Всего возможно  ! перестановок карточек.
Заметим, что перестановка двух карточек с буквой А не меняет слова. Поэтому
есть
два благоприятных
исхода:
! перестановок карточек.
Заметим, что перестановка двух карточек с буквой А не меняет слова. Поэтому
есть
два благоприятных
исхода:  и
и  . Вероятность получить нужное слово равна
. Вероятность получить нужное слово равна  .
.
Пример 17. Игральная кость подбрасывается трижды. Найти вероятность получить в сумме четыре очка.
Решение. Общее
число равновозможных элементарных исходов есть  . Сумма
очков равна четырем, если на двух костях выпали единицы, и на одной -
двойка.
Этому событию благоприятствуют три элементарных
исхода:
. Сумма
очков равна четырем, если на двух костях выпали единицы, и на одной -
двойка.
Этому событию благоприятствуют три элементарных
исхода:  . Поэтому искомая вероятность
равна
. Поэтому искомая вероятность
равна  .
.
Результаты многих экспериментов нельзя описать дискретным множеством точек. Например, бросание монеты на стол в примере 4 приводит к пространству элементарных исходов, совпадающему с множеством точек стола. Дальность броска копья спортсменом - величина с положительными значениями на числовой прямой, и т.д. Рассмотрим один из способов задания вероятностей на таком пространстве исходов.

