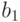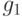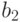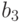Паросочетания и свадьбы
Паросочетания и свадьбы
Результаты этой главы носят более комбинаторный характер, чем результаты всех предыдущих глав, хотя они тесно связаны с теорией графов. Обсудим хорошо известную "теорему о свадьбах", принадлежащую Филиппу Холлу, и некоторые приложения этой теоремы, например, построение латинских квадратов.
Теорема Холла о свадьбах
Теорема о свадьбах, доказанная Филиппом Холлом в 1935 г., отвечает на
следующий вопрос, известный под названием задачи о свадьбах:
рассмотрим некоторое конечное множество юношей, каждый из которых знаком с
несколькими девушками; спрашивается, при каких условиях можно женить
юношей так, чтобы каждый из них женился на знакомой ему девушке?
(Будем считать, что полигамия не разрешена.) Например, если имеется четверо
юношей  и пять девушек
и пять девушек  , а отношения знакомства между ними показаны в таблице 1,
то возможно следующее решение:
, а отношения знакомства между ними показаны в таблице 1,
то возможно следующее решение:  женится
на
женится
на  ,
,  —
на
—
на 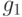 ,
, 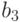 —
—  ,
а
,
а  — на
— на  .
.
Эту задачу можно представить графически, взяв двудольный
граф  с множеством вершин, разделенных на два непересекающихся подмножества
с множеством вершин, разделенных на два непересекающихся подмножества  , представляющих юношей и девушек, соответственно,
и соединив ребром каждого юношу со знакомой ему девушкой.
, представляющих юношей и девушек, соответственно,
и соединив ребром каждого юношу со знакомой ему девушкой.
Напомним определение двудольного графа. Допустим, что множество вершин
графа можно разбить на два непересекающихся подмножества 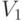 и
и 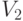 так, что каждое ребро в
так, что каждое ребро в  соединяет какую-нибудь вершину
из
соединяет какую-нибудь вершину
из 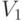 с какой-либо вершиной из
с какой-либо вершиной из 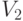 , тогда
, тогда  называем двудольным
графом. Такие графы иногда обозначают
называем двудольным
графом. Такие графы иногда обозначают 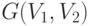 ,
если хотят выделить два указанных подмножества. Двудольный граф можно определить и
по-другому в терминах раскраски его вершин двумя цветами, скажем,
красным и синим. При этом граф называется двудольным, если каждую его
вершину можно окрасить красным или синим цветом так, чтобы любое ребро
имело один конец красный, а другой — синий. Следует подчеркнуть, что
в двудольном графе совсем не обязательно каждая вершина из
,
если хотят выделить два указанных подмножества. Двудольный граф можно определить и
по-другому в терминах раскраски его вершин двумя цветами, скажем,
красным и синим. При этом граф называется двудольным, если каждую его
вершину можно окрасить красным или синим цветом так, чтобы любое ребро
имело один конец красный, а другой — синий. Следует подчеркнуть, что
в двудольном графе совсем не обязательно каждая вершина из 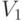 соединена с каждой вершиной из
соединена с каждой вершиной из 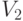 ; если же это так и если при
этом граф
; если же это так и если при
этом граф  , простой, то он называется полным двудольным графом
и обычно обозначается
, простой, то он называется полным двудольным графом
и обычно обозначается 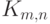 , где
, где 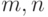 —
число вершин, соответственно, в
—
число вершин, соответственно, в 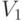 и
и 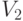 .
.
Совершенным
паросочетанием из 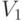 в
в 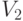 в двудольном графе
в двудольном графе 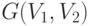 называется взаимно однозначное соответствие между вершинами из
называется взаимно однозначное соответствие между вершинами из 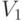 и подмножеством
вершин из
и подмножеством
вершин из 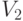 , обладающее тем свойством, что соответствующие вершины
соединены ребром. Ясно, что задачу о свадьбах можно выразить в терминах
теории графов следующим образом: если
, обладающее тем свойством, что соответствующие вершины
соединены ребром. Ясно, что задачу о свадьбах можно выразить в терминах
теории графов следующим образом: если  —
двудольный граф, то при каких условиях в
—
двудольный граф, то при каких условиях в  существует совершенное
паросочетание из
существует совершенное
паросочетание из 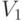 в
в 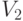 ?
?
Используя прежнюю "матримониальную" терминологию, можно
сформулировать следующее очевидное утверждение: необходимое условие для существования решения
в задаче о свадьбах в том, что
любые  юношей из данного множества должны быть
знакомы (в совокупности ), по
меньшей мере, с
юношей из данного множества должны быть
знакомы (в совокупности ), по
меньшей мере, с  девушками (для всех целых
девушками (для всех целых  , удовлетворяющих
неравенствам
, удовлетворяющих
неравенствам 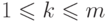 , где через
, где через  обозначено общее число юношей).
Необходимость этого условия сразу
вытекает из того, что если оно не верно для какого-нибудь множества
юношей, то мы не сможем женить требуемым способом даже
этих
обозначено общее число юношей).
Необходимость этого условия сразу
вытекает из того, что если оно не верно для какого-нибудь множества
юношей, то мы не сможем женить требуемым способом даже
этих  юношей, не говоря уже об остальных.
юношей, не говоря уже об остальных.