Теорема Цермело
Теорема Цермело
Теорема 24.(Цермело) Всякое множество может быть вполне упорядочено.
Доказательство.
Доказательство этой теоремы существенно использует аксиому
выбора и вызывало большие нарекания
своей неконструктивностью.
На счетных множествах полный порядок указать легко
(перенеся с 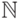 ). Но уже на множестве действительных
чисел никакого конкретного полного порядка указать не удается, и
доказав (с помощью аксиомы выбора) его существование, мы так и
не можем себе этот порядок представить.
). Но уже на множестве действительных
чисел никакого конкретного полного порядка указать не удается, и
доказав (с помощью аксиомы выбора) его существование, мы так и
не можем себе этот порядок представить.
Объясним, в какой форме используется аксиома
выбора. Пусть  - данное нам множество. Мы принимаем, что
существует функция
- данное нам множество. Мы принимаем, что
существует функция  , определенная на всех подмножествах
множества
, определенная на всех подмножествах
множества  , кроме самого
, кроме самого  , которая указывает
один из элементов вне этого подмножества:
, которая указывает
один из элементов вне этого подмножества:
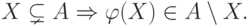
После того, как такая функция фиксирована, можно построить
полный порядок на  , и в этом построении уже нет никакой
неоднозначности. Вот как это делается.
, и в этом построении уже нет никакой
неоднозначности. Вот как это делается.
Наименьшим элементом множества  мы объявим
элемент
мы объявим
элемент 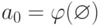 . За ним идет
элемент
. За ним идет
элемент  ; по построению он отличается
от
; по построению он отличается
от 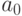 .
Далее следует
элемент
.
Далее следует
элемент 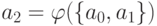 . Если
множество
. Если
множество  бесконечно, то такой процесс можно продолжать и
получить последовательность
бесконечно, то такой процесс можно продолжать и
получить последовательность 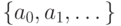 элементов
множества
элементов
множества  . Если после этого остаются еще не использованные
элементы множества
. Если после этого остаются еще не использованные
элементы множества  , рассмотрим элемент
, рассмотрим элемент 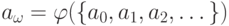 и так будем продолжать,
пока все
и так будем продолжать,
пока все  не кончится; когда оно кончится, порядок выбора
элементов и будет полным порядком на
не кончится; когда оно кончится, порядок выбора
элементов и будет полным порядком на  .
.
Конечно, последняя фраза нуждается в уточнении - что значит "
так будем продолжать"? Возникает желание применить теорему о
трансфинитной рекурсии (у нас очень похожая ситуация: следующий
элемент определяется рекурсивно, если известны все предыдущие).
И это можно сделать, если у нас есть другое вполне упорядоченное
множество  , и получить взаимно однозначное соответствие
либо между
, и получить взаимно однозначное соответствие
либо между  и частью
и частью  , либо между
, либо между  и
частью
и
частью  . В
первом случае все хорошо, но для этого надо иметь вполне
упорядоченное множество
. В
первом случае все хорошо, но для этого надо иметь вполне
упорядоченное множество  по крайней мере той же мощности, что
и
по крайней мере той же мощности, что
и  , так что получается некий порочный круг.
, так что получается некий порочный круг.
Тем не менее из него можно выйти. Мы сделаем это так: рассмотрим все потенциальные кусочки будущего порядка и убедимся, что их можно склеить.
Пусть 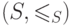 - некоторое подмножество
множества
- некоторое подмножество
множества  и заданный на нем порядок. Будем говорить, что
и заданный на нем порядок. Будем говорить, что 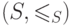 является корректным фрагментом, если оно является
вполне упорядоченным множеством, причем
является корректным фрагментом, если оно является
вполне упорядоченным множеством, причем
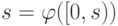
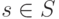 . Здесь
. Здесь 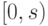 - начальный отрезок
множества
- начальный отрезок
множества  , состоящий из всех элементов, меньших
, состоящий из всех элементов, меньших  с точки зрения заданного на
с точки зрения заданного на  порядка.
порядка.Например, множество 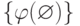 является
корректным фрагментом (порядок здесь можно не указывать, так как
элемент всего один). Множество
является
корректным фрагментом (порядок здесь можно не указывать, так как
элемент всего один). Множество 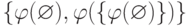 (первый из выписанных
элементов считается меньшим второго) также является корректным
фрагментом. Это построение можно продолжать и дальше, но нам
надо каким-то образом " перескочить" через бесконечное (и
очень большое в смысле мощности) число шагов этой конструкции.
(первый из выписанных
элементов считается меньшим второго) также является корректным
фрагментом. Это построение можно продолжать и дальше, но нам
надо каким-то образом " перескочить" через бесконечное (и
очень большое в смысле мощности) число шагов этой конструкции.
План такой: мы докажем, что любые два корректных фрагмента
в определенном смысле согласованы, после чего
рассмотреть объединение всех корректных фрагментов. Оно
будет корректным и будет совпадать со всем множеством  (в противном случае его можно было бы расширить и получить
корректный фрагмент, не вошедший в объединение).
(в противном случае его можно было бы расширить и получить
корректный фрагмент, не вошедший в объединение).
Лемма 1. Пусть 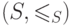 и
и 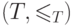 -
два корректных
фрагмента. Тогда один из них является начальным отрезком
другого, причем порядки согласованы (два общих элемента
все равно как сравнивать - в смысле
-
два корректных
фрагмента. Тогда один из них является начальным отрезком
другого, причем порядки согласованы (два общих элемента
все равно как сравнивать - в смысле  или в
смысле
или в
смысле 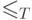 ).
).
Заметим, что по теореме 20 один из
фрагментов изоморфен начальному отрезку другого. Пусть  изоморфен начальному отрезку
изоморфен начальному отрезку  и
и  -
их изоморфизм. Лемма утверждает, что изоморфизм
-
их изоморфизм. Лемма утверждает, что изоморфизм  является тождественным, то есть что
является тождественным, то есть что 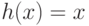 при
всех
при
всех 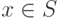 . Докажем это индукцией по
. Докажем это индукцией по 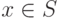 (это законно, так
как
(это законно, так
как  вполне
упорядочено по определению корректного фрагмента).
Индуктивное предположение гарантирует, что
вполне
упорядочено по определению корректного фрагмента).
Индуктивное предположение гарантирует, что 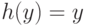 для
всех
для
всех 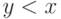 .
Мы хотим доказать, что
.
Мы хотим доказать, что 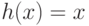 . Рассмотрим начальные
отрезки
. Рассмотрим начальные
отрезки 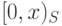 и
и 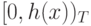 (с точки зрения
порядков
(с точки зрения
порядков  и
и 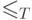 соответственно).
Они соответствуют друг другу
при изоморфизме
соответственно).
Они соответствуют друг другу
при изоморфизме  , поэтому по предположению индукции совпадают
как множества. Но по определению корректности
, поэтому по предположению индукции совпадают
как множества. Но по определению корректности 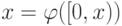 и
и  , так что
, так что 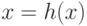 .
Лемма 1 доказана.
.
Лемма 1 доказана.
Рассмотрим объединение всех корректных фрагментов (как множеств). На этом объединении естественно определен линейный порядок: для всяких двух элементов найдется фрагмент, которому они оба принадлежат (каждый принадлежит своему, возьмем больший из фрагментов), так что их можно сравнить. По лемме 1 порядок не зависит от того, какой фрагмент будет выбран для сравнения.
Лемма 2. Это объединение будет корректным фрагментом.
Чтобы доказать лемму 2, заметим, что на этом объединении
определен линейный порядок. Он
будет полным. Для разнообразия объясним это в терминах
убывающих последовательностей. Пусть  ; возьмем корректный фрагмент
; возьмем корректный фрагмент  , которому
принадлежит
, которому
принадлежит  . Из леммы 1 следует, что все
. Из леммы 1 следует, что все  также
принадлежат этому фрагменту (поскольку фрагмент
также
принадлежат этому фрагменту (поскольку фрагмент  будет
начальным отрезком в любом большем фрагменте),
а
будет
начальным отрезком в любом большем фрагменте),
а  вполне упорядочен по
определению, так что последовательность стабилизируется. Лемма 2
доказана.
вполне упорядочен по
определению, так что последовательность стабилизируется. Лемма 2
доказана.
Утверждение леммы 2 можно переформулировать таким образом:
существует наибольший
корректный фрагмент. Осталось доказать, что этот фрагмент
(обозначим его  ) включает в себя все множество
) включает в себя все множество  .
Если
.
Если 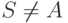 , возьмем элемент
, возьмем элемент 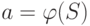 , не
принадлежащий
, не
принадлежащий  ,
и добавим его к
,
и добавим его к  , считая, что он больше всех
элементов
, считая, что он больше всех
элементов  . Полученное упорядоченное множество
. Полученное упорядоченное множество 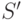 (сумма
(сумма  и одноэлементного множества) будет, очевидно,
вполне упорядочено. Кроме того, условие корректности
также выполнено (для
и одноэлементного множества) будет, очевидно,
вполне упорядочено. Кроме того, условие корректности
также выполнено (для  - по построению, для остальных
элементов - поскольку оно было выполнено в
- по построению, для остальных
элементов - поскольку оно было выполнено в  ).
Таким образом, мы построили больший корректный фрагмент,
что противоречит максимальности
).
Таким образом, мы построили больший корректный фрагмент,
что противоречит максимальности  . Это рассуждение
завершает доказательство теоремы Цермело.
. Это рассуждение
завершает доказательство теоремы Цермело.
Как мы уже говорили, из теоремы Цермело и теоремы 20 о сравнении вполне упорядоченных множеств немедленно вытекает такое утверждение:
Теорема 25. Из любых двух множеств одно равномощно подмножеству другого.
Понятие вполне упорядоченного множества ввел Кантор в работе 1883 года; в его итоговой работе 1895-1897 годов приводится доказательство того, что любые два вполне упорядоченных множества сравнимы (одно изоморфно начальному отрезку другого).
Утверждения о возможности полного упорядочения любого множества и о сравнении мощностей (теоремы 24 и 25) неоднократно встречаются в работах Кантора, но никакого внятного доказательства он не предложил, и оно было дано лишь в 1904 году немецким математиком Э.Цермело.
