Операции над мощностями
Мощности конечных множеств - натуральные числа, и их можно складывать, умножать, возводить в степень. Эти операции можно обобщить и на мощности бесконечных множеств, и делается это так.
Пусть  и
и  - два множества. Чтобы сложить их
мощности, надо
взять мощность
множества
- два множества. Чтобы сложить их
мощности, надо
взять мощность
множества 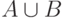 , если
, если  и
и  не
пересекаются. Если они
пересекаются, то их надо заменить на непересекающиеся
равномощные им множества
не
пересекаются. Если они
пересекаются, то их надо заменить на непересекающиеся
равномощные им множества 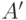 и
и  . Мощность
объединения и
будет суммой
мощностей множеств
. Мощность
объединения и
будет суммой
мощностей множеств  и
и  .
.
Замечания.
- Чтобы избежать упоминания мощностей как
самостоятельных объектов, следует считать выражение " мощность
множества
 есть сумма мощностей множеств
есть сумма мощностей множеств  и
и  "
идиоматическим выражением (а сказанное выше - его определением).
Но мы для удобства будем часто пренебрегать такими
предосторожностями.
"
идиоматическим выражением (а сказанное выше - его определением).
Но мы для удобства будем часто пренебрегать такими
предосторожностями. - В принципе следовало бы проверить корректность этого
определения и доказать, что мощность множества
 не
зависит от того, какие именно непересекающиеся
множества
не
зависит от того, какие именно непересекающиеся
множества 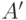 и
и  (равномощные
(равномощные  и
и  ) мы выберем. (Что, впрочем,
очевидно.)
) мы выберем. (Что, впрочем,
очевидно.) - Для конечных множеств получается обычное сложение натуральных чисел.
- Наконец, формально следовало бы еще доказать, что такие
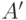 и
и  можно выбрать. Это можно сделать, например, так: положим
можно выбрать. Это можно сделать, например, так: положим 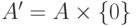 и
и  .
.
Последней проблемы не будет при определении произведения
мощностей как мощности декартова произведения  (Но остальные замечания остаются в силе.)
(Но остальные замечания остаются в силе.)
Теперь определим возведение в степень.
Для этого рассмотрим (для данных  и
и  ) множество
всех функций
вида
) множество
всех функций
вида 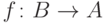 (напомним: это означает, что их область определения есть
(напомним: это означает, что их область определения есть  , а
область значений содержится в
, а
область значений содержится в  ). Это множество
обозначается
). Это множество
обозначается 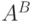 , и его мощность и будет результатом операции возведения в степень.
, и его мощность и будет результатом операции возведения в степень.
Если множества  и
и  конечны и содержат
конечны и содержат  и
и  элементов
соответственно, то
элементов
соответственно, то 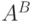 содержит как раз
содержит как раз  элементов. В
самом деле, определяя функцию
элементов. В
самом деле, определяя функцию 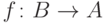 , мы должны
определить
ее значение на каждом из
, мы должны
определить
ее значение на каждом из  элементов. Это можно сделать
элементов. Это можно сделать  способами,
так что получаем всего
способами,
так что получаем всего  вариантов.
вариантов.
66. Чему равно  согласно нашему определению?
согласно нашему определению?
Пример. Обозначим через  какое- нибудь множество из
двух
элементов, например,
какое- нибудь множество из
двух
элементов, например,  . Что
такое
. Что
такое 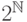 ? По
определению это множество функций
? По
определению это множество функций 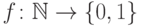 .
Такие функции - это по существу последовательности нулей и
единиц, только вместо
.
Такие функции - это по существу последовательности нулей и
единиц, только вместо 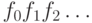 мы пишем
мы пишем 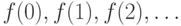 (Формально последовательность элементов
некоторого множества
(Формально последовательность элементов
некоторого множества  так и определяется - как функция
типа
так и определяется - как функция
типа 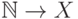 .)
.)
Заметим, что 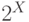 равномощно
равномощно 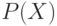 (в
частном случае
(в
частном случае  мы это доказывали; для общего случая доказательство такое же).
мы это доказывали; для общего случая доказательство такое же).
Обычные свойства сложения и умножения (коммутативность, ассоциативность и дистрибутивность) сохраняют силу и для арифметики мощностей:
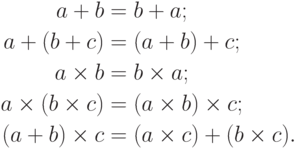
Формально их следует читать, избегая слова " мощность"
как самостоятельного объекта: например,  означает, что
означает, что  и
и  равномощны
(и это легко
проверить:
равномощны
(и это легко
проверить:  будет
взаимно однозначным соответствием между ними). Остальные свойства
доказываются столь же просто. Чуть сложнее свойства,
включающие возведение в степень:
будет
взаимно однозначным соответствием между ними). Остальные свойства
доказываются столь же просто. Чуть сложнее свойства,
включающие возведение в степень:
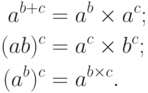
Проверим первое из них. Из чего состоит 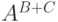 ? (Будем
считать, что
? (Будем
считать, что  и
и  не пересекаются.) Его элементами
являются
функции со значениями в
не пересекаются.) Его элементами
являются
функции со значениями в  , определенные на
, определенные на  .
Такая функция состоит из двух частей: своего сужения на
.
Такая функция состоит из двух частей: своего сужения на  (значения на аргументах из
(значения на аргументах из  остаются теми же, остальные
отбрасываются) и своего сужения на
остаются теми же, остальные
отбрасываются) и своего сужения на  . Тем самым для каждого
элемента множества
. Тем самым для каждого
элемента множества 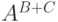 мы получаем пару элементов
из
мы получаем пару элементов
из 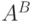 и
и 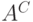 . Это и будет искомое взаимно однозначное
соответствие.
. Это и будет искомое взаимно однозначное
соответствие.
С соответствием между множествами 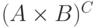 и
и  мы тоже
часто сталкиваемся. Например, элемент
множества
мы тоже
часто сталкиваемся. Например, элемент
множества 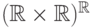 есть отображение типа
есть отображение типа  , то есть кривая
, то есть кривая 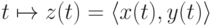 на плоскости. Такая
кривая задается парой функций
на плоскости. Такая
кривая задается парой функций  .
.
Соответствие между  и
и 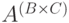 встречается
несколько реже. Элемент
встречается
несколько реже. Элемент 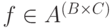 является
отображением
является
отображением 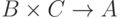 , то есть, в обычной
терминологии,
функцией двух аргументов (первый из
, то есть, в обычной
терминологии,
функцией двух аргументов (первый из  , второй из
, второй из  ).
Если
зафиксировать в ней второй аргумент, то получится
функция
).
Если
зафиксировать в ней второй аргумент, то получится
функция 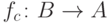 , определенная
соотношением
, определенная
соотношением 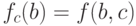 (точнее,
(точнее, 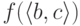 ). Отображение
). Отображение  ,
принадлежащее
,
принадлежащее  , и соответствует
элементу
, и соответствует
элементу 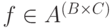 .
(Отчасти сходная конструкция встречается в
алгебре, когда многочлен от двух переменных рассматривают как
многочлен от одной переменной с коэффициентами в кольце многочленов
от второй переменной.)
.
(Отчасти сходная конструкция встречается в
алгебре, когда многочлен от двух переменных рассматривают как
многочлен от одной переменной с коэффициентами в кольце многочленов
от второй переменной.)
Мощность счетного множества символически обозначается  мощность континуума (отрезка или множества бесконечных последовательностей
нулей и единиц)
обозначается
мощность континуума (отрезка или множества бесконечных последовательностей
нулей и единиц)
обозначается 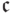 .
По определению,
.
По определению, 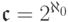 .
.
(Естественный вопрос: каков смысл индекса  в
в 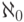 ?
что такое, скажем,
?
что такое, скажем, 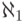 ? Обычно
? Обычно 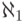 обозначает
наименьшую несчетную мощность (как мы увидим, такая существует).
Гипотеза континуума, о которой мы упоминали ранее, утверждает,
что
обозначает
наименьшую несчетную мощность (как мы увидим, такая существует).
Гипотеза континуума, о которой мы упоминали ранее, утверждает,
что  .)
.)
Известные нам свойства счетных множеств можно записать так:
-
 для конечного
для конечного  (объединение счетного
и конечного множеств счетно);
(объединение счетного
и конечного множеств счетно); -
 (объединение двух
счетных множеств
счетно);
(объединение двух
счетных множеств
счетно); -
 (объединение
счетного числа
счетных множеств счетно).
(объединение
счетного числа
счетных множеств счетно).
Отсюда можно формально получить многие факты манипуляциями с мощностями. Например, цепочка равенств

Аналогичным образом,

67. Объясните подробно выкладку:
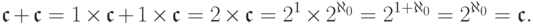
68. Проверьте, что  .
.
Приведенные нами свойства мощностей полезно сочетать с теоремой Кантора- Бернштейна. Например, заметим, что
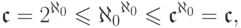
 (словами: множество всех бесконечных последовательностей
натуральных чисел имеет мощность континуума).
(словами: множество всех бесконечных последовательностей
натуральных чисел имеет мощность континуума).69. Последнее рассуждение неявно использует монотонность операции
возведения в степень для мощностей (если  ,
то
,
то 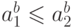 ). Проверьте это и аналогичные свойства для других
операций (впрочем, почти очевидные).
). Проверьте это и аналогичные свойства для других
операций (впрочем, почти очевидные).
70. Установите явное соответствие между последовательностями
натуральных чисел и иррациональными числами на отрезке 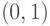 ,
используя цепные дроби, то есть дроби вида
,
используя цепные дроби, то есть дроби вида  .
.
71. Проверьте, что  .
(Напомним, что по теореме Кантора эта мощность больше
мощности континуума.)
.
(Напомним, что по теореме Кантора эта мощность больше
мощности континуума.)
72. Какова мощность множества всех непрерывных функций с действительными аргументами и значениями? Существенна ли здесь непрерывность?
73. Какова мощность множества всех монотонных функций с действительными аргументами и значениями?
74. Может ли семейство подмножеств натурального ряда быть несчетным, если любые два его элемента имеют конечное пересечение? конечную симметрическую разность?
Впоследствии мы увидим, что для бесконечных мощностей 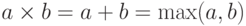 , но пока этого мы доказать не можем. Поэтому
в задачах 47, 48, нам
пришлось воспользоваться обходным маневром, чтобы доказать, что
из
, но пока этого мы доказать не можем. Поэтому
в задачах 47, 48, нам
пришлось воспользоваться обходным маневром, чтобы доказать, что
из  следует
следует 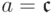 или
или  . Следующее утверждение обобщает этот прием:
. Следующее утверждение обобщает этот прием:
Теорема 10.
Если множество  разбито на
непересекающиеся
части
разбито на
непересекающиеся
части 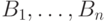 , то найдется такое
, то найдется такое  , при
котором
мощность
, при
котором
мощность  не меньше мощности
не меньше мощности  .
.
Доказательство.
В самом деле, рассмотрим проекцию множества  на
на  . Если хотя бы при
одном
. Если хотя бы при
одном  она покрывает
она покрывает  полностью, то все доказано. Если нет,
выберем для каждого
полностью, то все доказано. Если нет,
выберем для каждого  непокрытую точку
непокрытую точку  . Набор
. Набор 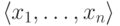 не входит ни в одно из множеств
не входит ни в одно из множеств  ,
что
противоречит предположению.
,
что
противоречит предположению.
Заметим, что в формулировке этого утверждения (которое иногда
называют теоремой Кенига)
говорится о декартовом
произведении конечного числа множеств, которое можно определить
индуктивно (скажем, 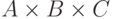 будет состоять из
троек
будет состоять из
троек 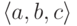 , которые суть пары
, которые суть пары 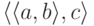 ). Декартово произведение счетного числа
множеств уже так не определишь. Выход такой:
). Декартово произведение счетного числа
множеств уже так не определишь. Выход такой:  (счетное число
сомножителей) можно определить
как множество всех
последовательностей
(счетное число
сомножителей) можно определить
как множество всех
последовательностей 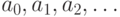 , у которых
, у которых 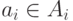 , то есть как множество всех функций
, то есть как множество всех функций  , определенных
на
, определенных
на 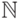 со значениями в объединении всех
со значениями в объединении всех  , причем
, причем  при всех
при всех  . После такого определения
теорема 10 легко переносится и
на счетные
(а также и на любые) произведения.
. После такого определения
теорема 10 легко переносится и
на счетные
(а также и на любые) произведения.
Переходя к отрицаниям, теорему Кенига можно сформулировать так:
если при всех 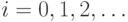 для мощностей
для мощностей  и
и 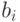 выполнено неравенство
выполнено неравенство 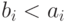 , то
, то
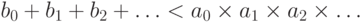
Учитывая, что 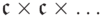 (счетное произведение) равно
(счетное произведение) равно 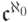 ,
то есть
,
то есть 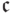 , можно сформулировать такое следствие
теоремы Кенига: если континуум разбит на счетное число
подмножеств, то одно из них имеет мощность континуума.
, можно сформулировать такое следствие
теоремы Кенига: если континуум разбит на счетное число
подмножеств, то одно из них имеет мощность континуума.
75. Докажите подробно это утверждение.
76. Пусть 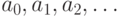 - мощности, причем
- мощности, причем  для всех
для всех  .
Покажите, что
.
Покажите, что

77. Пусть  - возрастающая
последовательность
мощностей. Докажите, что сумма
- возрастающая
последовательность
мощностей. Докажите, что сумма  не
представима
в виде
не
представима
в виде 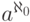 ни для какой мощности
ни для какой мощности  .
.
