Муравьиные алгоритмы
12.6 Q-муравьиная система
В [10] разработана модификация СМК (в современной классификации – Ant-Q), в которой правило локального изменения концентрации феромона реализовано на основе метода Q-обучения (Q-learning).
Пусть 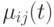 обозначает AQ-значение дуги
обозначает AQ-значение дуги  в момент
в момент  . Тогда правило перехода для этой дуги определяется следующим образом
. Тогда правило перехода для этой дуги определяется следующим образом
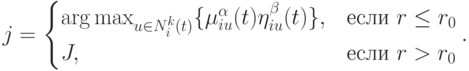 |
( 12.25) |
Здесь коэффициенты 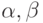 определяют важность AQ-величин
определяют важность AQ-величин  и эвристической информации . AQ-величины отражают предпочтительность перехода
и эвристической информации . AQ-величины отражают предпочтительность перехода  . В уравнении (12.25)
. В уравнении (12.25)  – случайная переменная, значение которой выбирается в соответствии с распределением, которое определяется функцией AQ-величин
– случайная переменная, значение которой выбирается в соответствии с распределением, которое определяется функцией AQ-величин 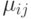 и
и  . Предложено три различных правила для выбора значения
. Предложено три различных правила для выбора значения  :
:
- псевдослучайный выбор, где следующая вершина
 случайным образом выбирается из множества
случайным образом выбирается из множества 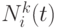 в соответствии с однородным распределением;
в соответствии с однородным распределением; -
псевдослучайный пропорциональный выбор, где
 выбирается в соответствии со следующим распределением
выбирается в соответствии со следующим распределением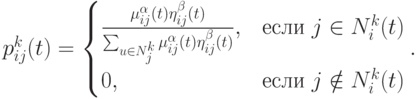
( 12.26) -
случайный пропорциональный выбор соответственно (12.25) с
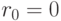 .В [10] отмечено, что псевдослучайный пропорциональный выбор лучше показал себя при решении задачи коммивояжера.
.В [10] отмечено, что псевдослучайный пропорциональный выбор лучше показал себя при решении задачи коммивояжера.AQ-величины обучаются с использованием следующих правил коррекции:
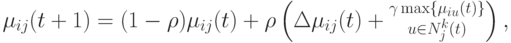
( 12.27) где
 -коэффициент переоценки (по аналогии с испарением феромона) и
-коэффициент переоценки (по аналогии с испарением феромона) и  - шаг обучения. Отметим, что при
- шаг обучения. Отметим, что при 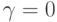 уравнение (12.27) сводится к уравнению (12.19) . В Ant-Q уравнение (12.27) применяется для каждого муравья после каждого нового выбора
уравнение (12.27) сводится к уравнению (12.19) . В Ant-Q уравнение (12.27) применяется для каждого муравья после каждого нового выбора  , но с
, но с 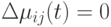 . Эффект заключается в том, что AQ-величины, связанные с дугой
. Эффект заключается в том, что AQ-величины, связанные с дугой  , уменьшаются путем умножения на
, уменьшаются путем умножения на  каждый раз, когда дуга выбирается в потенциальное решение. В тоже время AQ-величина корректируется пропорционально AQ-величине лучшей дуги
каждый раз, когда дуга выбирается в потенциальное решение. В тоже время AQ-величина корректируется пропорционально AQ-величине лучшей дуги  .
.
