НОУ ИНТУИТ | Эволюционные вычисления. Лекция 12: Муравьиные алгоритмы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет путей сообщения

Опубликован: 10.10.2014 | Доступ: свободный | Студентов: 869 / 193 | Длительность: 22:10:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист, Архитектор программного обеспечения

|

Вам нравится? Нравится 18 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

12.5 Максиминная муравьиная система

Данная модификация (макси-минная муравьиная система МММС - Max-MinAntSystem [8]) разработана для преодоления проблемы преждевременной стагнации. Ее основное отличие от МС в том, что интенсивность феромона ограничивается в некотором заданном интервале. Кроме этого, здесь изменять концентрацию феромона разрешается только лучшим муравьям, начальная концентрация феромона устанавливается в максимально допустимые значения и используется механизм сглаживания для концентрации феромона.

В МММС концентрация феромона изменяется, также как и в СМК, согласно уравнению (12.19), где 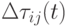$\Delta\tau_{ij}(t)$ вычисляется на основе либо глобально, либо лучшего на итерации пути. Первая версия МММС использовала при коррекции феромона лучший на текущей итерации путь 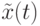$\tilde x(t)$ , последние версии основаны на применении глобально лучшего пути 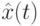$\hat x(t)$ с различными стратегиями:

Использование только глобально лучшего пути 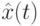$\hat x(t)$ для определения концентрации 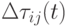$\Delta\tau_{ij}(t)$ , что ускоряет процесс поиска, но с другой стороны сужает его.
Использование смешанных стратегий, где для коррекции концентрации феромона используются как 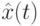$\hat x(t)$ , так и 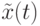$\tilde x(t)$ . При этом для расширения пространства поиска, в основном, применяется лучший за текущую итерацию путь с периодическим подключением глобально лучший путь. Обычно частота использования последнего увеличивается в процессе поиска.
В случае стагнации все значения концентрации феромона $\tau_{ij}$ реинициализируются до допустимых максимальных значений, после чего допускается использовать только лучший за текущую итерацию путь ограниченное число итераций.

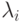Для определения точки стагнации используется коэффициент $\lambda$ -ветвления [9] со значением $\lambda=0,05$ . При этом $\lambda_i$ определяется как число дуг, исходящих из узла со значением $\tau_{ij}$ больше чем $\lambda\delta_i+\tau_{i,\min};\delta_i=\tau_{i,\max}-\tau_{i,\min}$ , где

$\tau_{i,\min}=\substack{\min\{\tau_{ij}\}\\j\in N_i}$

( 12.22)

$\tau_{i,\min}=\substack{\max\{\tau_{ij}\}\\j\in N_i}$

( 12.23)

и N_i - множество узлов, соединенных с узлом . Если

$\frac{\sum_{i\in V}\lambda_i}{n_G}<\varepsilon,$

( 12.24)

где $\varepsilon$ - малое положительное значение, то предполагается, что наступила стагнация в процессе поиска.

В процессе поиска в МММС все значения концентрации феромона $\tau_{ij}$ ограничены в заданном диапазоне. В первой версии МММС $\tau_{ij}\in[\tau_{\min},\tau_{\max}]$ для всех дуг (i,j) , где границы диапазона $\tau_{\min},\tau_{\max}]$ постоянны и зависят от решаемой задачи. Если после коррекции концентрации феромона имеем $\tau_{ij}(t+1)>\tau_{\max}$ , то полагаем $\tau_{ij}(t+1)=\tau_{\max}$ . Аналогично при $\tau_{ij}(t+1)<\tau_{\min}\ \tau_{ij}(t+1)=\tau_{\min}$ . Ограничение значений концентрации иногда позволяет избежать стагнации. В целом алгоритм представлен псевдокодом А12.5[4].

Дальше >>

Авторизоваться

Эволюционные вычисления

Муравьиные алгоритмы

12.5 Максиминная муравьиная система

Вопросы и ответы