Муравьиные алгоритмы

12.13 Применение муравьиных алгоритмов

Муравьиные алгоритмы использовались при решении многих реальных задач, прежде всего задач комбинаторной оптимизации, из которых самой "популярной" является задача коммивояжера. Для того чтобы разработать муравьиный алгоритм для решения конкретной задачи, необходимо:

1. Соответствующее представление в виде графа для описания дискретного пространства поиска. Граф должен представлять все состояния и переходы между ними. Необходима также схема представления потенциального решения.
2. Определить правила коррекции концентрации феромона, которые определяют положительную обратную связь в процессе.
3. При необходимости разработать эвристику для определения предпочтительности дуги в графе.
4. Определить эвристику поведения муравья при построении решения в виде вероятности перехода.
5. Определить средства проверки выполнимости потенциального решения с учетом ограничений задачи.
6. Определить основные параметры МА (число искусственных муравьев и т.п.).

Далее рассмотрим использование МА на примере задачи коммивояжера, на которой впервые были апробированы МА. Напомним, что формальная постановка этой задачи изложена в разделе 3. Здесь мы имеем естественное представление задачи в виде графа , где –множество вершин, каждая из которых представляет город, множество дуг графа представляет связи между городами и - матрица расстояний, где каждой дуге приписывается вес .

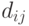Предпочтительность выбора вершины после в данном случае естественно определить как 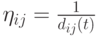, где время существенно только для задач с изменяющимся окружением.

Решение задачи должно удовлетворять двум ограничениям: 1) все города должны быть посещены, 2) каждый город разрешается посещать только один раз. Для проверки второго ограничения часто используется tabu-список для каждого потенциального решения, где содержатся посещенные города. Пусть обозначает tabu-список для -го муравья (потенциального решения). Тогда 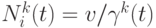- множество непосещенных городов после достижения города .

При решении задачи каждое потенциальное решение представляется искусственным муравьем. При инициализации муравьи располагаются на городах случайным образом и далее каждый муравей строит свое решение путем выбора в текущей вершине следующей вершины , используя вероятность перехода в соответствии с одним из представленных выше вариантов МА.

Поскольку в основе МА лежит передвижение муравьев по некоторым путям, то МА эффективны, прежде всего, при решении задач, которые допускаю интерпретацию в виде графа. Проведенные многочисленные компьютерные эксперименты показали, что эффективность МА растет при увеличении размерности задачи и для задач на графах высокой размерности они работают быстрее, чем другие эволюционные алгоритмы.Отмечены также хорошие результаты при решении нестационарных задач на графах с изменяющейся средой.

В настоящее время муравьиные алгоритмы получили применение при решении следующих практических задач [3]:

1. маршрутизация (прежде всего, в сетях – networkrooting);
2. задачиназначения (quadratic assignment problem, graph coloring, generalized assignment, frequentially assignment);
3. машинноеобучение (classification rules, Bayesian networks, fuzzy systems);
4. кластеризация данных;
5. роботика (vehiclerouting и др. );
6. календарноепланированиеисоставлениерасписания( job shop, open shop, flow shop, total terdiness, project sheduling, group shop);
7. покрытиемножества, задачаобукладкерюкзака(multi-knapsack, max independent set, reduncy allocation, set covering, maximum clique, weight constrained graph tree partition, bin packing);
8. биоинформатика;
9. обработка текстов.

Этот список можно продолжить, поскольку число публикаций с использованием МА последние десять лет быстро растет.