Муравьиные алгоритмы

12.7 Быстрая муравьиная система

Данная модификация (FastAntSystem [11]) первоначально разработана для решения квадратичной задачи о назначениях (quadratic assignment problem). В быстрой муравьиной системе (БМС) по сравнению с другими муравьиными алгоритмами используется популяция, состоящая из одного муравья, и другие правила коррекции феромона без испарения. Естественно, использование только одного муравья снижает вычислительную сложность алгоритма. В БМС применяется правило перехода (12.6) со значением коэффициента (эвристическая информация не используется). Таким образом, правило коррекции концентрации феромона следующее:

( 12.28)

где коэффициенты 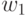и определяют относительный вклад текущего решения и лучшего глобального, которые вычисляются согласно

( 12.29)

( 12.30)

Здесь, как и ранее, 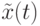и 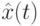представляют соответственнонайденный лучший путь на итерации и лучший путь в глобальном смысле (с первой по -ю итерацию). При инициализации 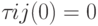. Когда найдено новое решение 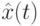, производится переинициализация .

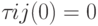12.8 Antabu

Эта модификация МС [12] включает локальный поиск с использованием tabu-поиска для улучшения решений, полученных на каждой итерации МС. Кроме этого, изменено глобальное правило пересчета концентрации феромона, где любой муравей откладывает феромон на каждой дуге пропорционально качеству пути согласно следующей формуле:

( 12.31)

где 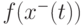- стоимость найденного худшего пути и 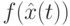- стоимость лучшего пути, найденного -м муравьем. Уравнение (12.31) применяется для каждого муравья и каждой дуги .