Эволюционное программирование
10.3.Применение классического эволюционного программирования в прогнозировании
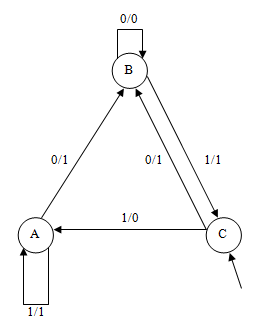
Как уже отмечалось, в ранних работах ЭП использовалось, в основном, при решении задач прогнозирования временных рядов, где целью эволюции популяции конечных автоматов является построение автомата, который способен предсказывать значение следующего входного сигнала. Рассмотрим суть задачи прогнозирования на примере автомата, представленного на рис.10.3 [1].
Задача заключается в определении следующего символа входной последовательности. Допустим приведенный автомат рис.10.3 находится в начальном состоянии  , и на его вход подается последовательность
, и на его вход подается последовательность  . В этом случае согласно графу переходов-выходов автомат выдает выходную последовательность
. В этом случае согласно графу переходов-выходов автомат выдает выходную последовательность  . Автомат правильно выполняет предсказание, если его выходной сигнал
. Автомат правильно выполняет предсказание, если его выходной сигнал 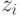 равен следующему входному сигналу
равен следующему входному сигналу  . В случае равенства
. В случае равенства  значение фитнесс-функции увеличивается на 1. Для нашего примера автомат правильно предсказывает 3 из 5 символов входной последовательности. .Иногда в фитнесс-функцию вводится штраф за превышение заданного числа состояний автомата.
значение фитнесс-функции увеличивается на 1. Для нашего примера автомат правильно предсказывает 3 из 5 символов входной последовательности. .Иногда в фитнесс-функцию вводится штраф за превышение заданного числа состояний автомата.
В качестве примера рассмотрим предсказание следующего символа периодической последовательности, один период которой представляется (101110011101)* [2]. Здесь входной и выходной алфавит конечных автоматов равен {0,1}. В качестве обучающего множества используется множество подпоследовательностей, содержащих первые 20 символов указанной циклической последовательности. Популяция случайным образом синтезированных конечных автоматов проходит пять поколений эволюции. В качестве фитнесс-функции в данном случае используется средняя абсолютная ошибка (число неправильно предсказанных символов). После короткого периода эволюции в популяции определялась лучшая особь (с минимальной ошибкой), которая далее использовалась для предсказания следующего символа входной последовательности. Такая процедура повторялась 300 раз, и процесс эволюции в итоге состоял из 1500 поколений. Процедура ЭП оценивалась при каждом прогнозе с использованием совокупной доли корректных прогнозов.
Эксперименты по прогнозированию выполнялись с популяциями, содержащими  особей. Число мутаций выбиралось случайным образом из
особей. Число мутаций выбиралось случайным образом из  . Было выполнено 30 попыток для каждой комбинации
. Было выполнено 30 попыток для каждой комбинации  и
и  . Число состояний автоматов варьировалось от 1 до 10. Во всех экспериментах максимальное число состояний ограничивалось сверху 10.
. Число состояний автоматов варьировалось от 1 до 10. Во всех экспериментах максимальное число состояний ограничивалось сверху 10.
Согласно [2] получены следующие результаты экспериментов для задачи прогнозирования, которые представлены на рис.10.4. Здесь показано, как изменяется доля правильных прогнозов для лучшего автомата в популяции, усредненная по 30 попыткам для популяций с числом особей 3,5,10,50 и 100 и выполнением от 1 до 3 операторов мутации. Из графика видно, что при первом прогнозе число правильных прогнозов примерно равно 80% (после 30 попыток первого эксперимента). Далее следует небольшой спад, и затем постепенное повышение доли правильных прогнозов примерно до 90%.