Эволюционное программирование
10.6. Параметры ЭП
К основным параметрам ЭП относится, прежде всего, размер шага мутации. В простейшем случае значения отклонения фиксируются и функция параметра линейна, т.е.  , где
, где 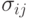 малая величина. Тогда потомок вычисляется в предположении Гауссова распределения
малая величина. Тогда потомок вычисляется в предположении Гауссова распределения 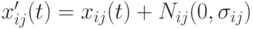 с
с 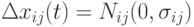 . Нотация
. Нотация  означает, что новое случайное значение генерируется для каждой компоненты каждой особи. Очевидным недостатком такого подхода является то, что слишком малые значения
означает, что новое случайное значение генерируется для каждой компоненты каждой особи. Очевидным недостатком такого подхода является то, что слишком малые значения 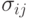 ограничивают пространство поиска и дают низкую скорость сходимости. С другой стороны, слишком большие значения
ограничивают пространство поиска и дают низкую скорость сходимости. С другой стороны, слишком большие значения 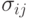 сдерживают "эксплуатацию" пространства поиска и способность точной доводки решения. Поэтому разработаны различные динамические стратегии изменения значений параметров.
сдерживают "эксплуатацию" пространства поиска и способность точной доводки решения. Поэтому разработаны различные динамические стратегии изменения значений параметров.
В одном из первых методов динамической настройки параметров его значение зависит от значения фитнесс-функции [6,13]:
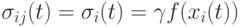 , где
, где ![\gamma \in(0,1]](/sites/default/files/tex_cache/a61d382e520d6a5c282d4824934a5f7f.png) и потомок
и потомок 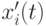 генерируется следующим образом
генерируется следующим образом 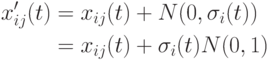 .
.
Если доступна информация о глобальном оптимуме, то вместо абсолютного значения фитнесс-функции можно использовать значение ошибки. Но, к сожалению, такая информация обычно недоступна. В качестве альтернативы можно использовать расстояние (на уровне фенотипа) от лучшей текущей особи, которое определяется выражением

где  - лучшая особь.
- лучшая особь.
Расстояние от лучшей текущей особи в пространстве решений также можно использовать для этих целей:
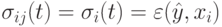
где 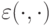 означает Евклидово расстояние между векторами. Преимущество этого подхода в том, что здесь чем хуже особь, тем больше шансов у нее мутировать. При этом потомок удаляется от худшей родительской особи. С другой стороны, чем лучше особь, тем потомок меньше удаляется от родительской особи, что позволяет "доводить" хорошее текущее решение. Но данный подход имеет следующие недостатки:
означает Евклидово расстояние между векторами. Преимущество этого подхода в том, что здесь чем хуже особь, тем больше шансов у нее мутировать. При этом потомок удаляется от худшей родительской особи. С другой стороны, чем лучше особь, тем потомок меньше удаляется от родительской особи, что позволяет "доводить" хорошее текущее решение. Но данный подход имеет следующие недостатки:
- для очень больших значений фитнесс-функции размер шага может также быть слишком большим, что чревато пропуском оптимума;
- проблема может быть даже в случае, когда худшее значение имеет большое ненулевое значение. Если значение фитнесс-функции хорошей особи также велико, размер шага может быть большим, что "уводит" особи от хороших решений. В таких случаях, если доступна информация об оптимуме, лучше использовать значение ошибки.
Предложено достаточно много способов управления размером шага, когда этот размер является некоторой функцией от значений фитнесс-функции и ниже приведены некоторые методы:
- Фогель [9] предложил аддитивный подход, где
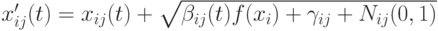 ,а
,а 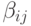 и
и  - коэффициенты пропорциональности и сдвига.
- коэффициенты пропорциональности и сдвига. - Для функции
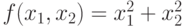 в [14] предложено
в [14] предложено 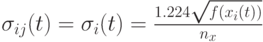 ,где
,где  - размерность пространства поиска
- размерность пространства поиска 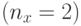 .
.
- Для обучения рекуррентных нейронных сетей в [15] используется
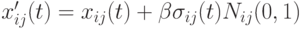 , где
, где  - коэффициент пропорциональности и
- коэффициент пропорциональности и ![sigma_{ij}(t)=U(0,1)\left[1-\frac{f(x_i(t))}{f_{\max}(t)}\right]](/sites/default/files/tex_cache/8ff1fb16944e28e934a828428437d683.png) с максимальным значением
с максимальным значением  текущей популяции (здесь рассматривается случай максимизации и
текущей популяции (здесь рассматривается случай максимизации и 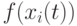 возвращает положительные значения).
возвращает положительные значения). - В работе [17] (для задач минимизации) используется отклонение, пропорциональное нормализованному значению фитнесс-функции
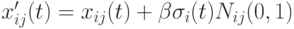 ,
где
,
где 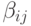 - коэффициент пропорциональности,
- коэффициент пропорциональности,  и
и  - мощность популяции.
- мощность популяции.
- В работе [17] (для задач максимизации) используется выражение
 , которое позволяет комбинировать граничные условия и фитнесс-функцию. Здесь
, которое позволяет комбинировать граничные условия и фитнесс-функцию. Здесь 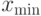 и
и  определяют границы диапазона изменения в пространстве поиска и параметр
определяют границы диапазона изменения в пространстве поиска и параметр  является малым числом.
является малым числом. - В [18] используется отклонение, пропорциональное расстоянию от лучшей особи
 ,где параметр
,где параметр  и коэффициент пропорциональности
и коэффициент пропорциональности 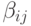 определяется следующим образом:
определяется следующим образом:  , где
, где ![\beta\in[0,2]](/sites/default/files/tex_cache/e6179231a234f7c135619ac71eeb29ea.png) и
и  определяет ширину пространства поиска как Евклидово расстояние между векторами
определяет ширину пространства поиска как Евклидово расстояние между векторами 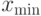 и
и  . При этом большие значения параметра
. При этом большие значения параметра  способствуют расширению пространства поиска, а малые значения – его эксплуатации. Иногда этот параметр изменяется со временем от больших начальных значений до малых конечных. При этом потомок генерируется так:
способствуют расширению пространства поиска, а малые значения – его эксплуатации. Иногда этот параметр изменяется со временем от больших начальных значений до малых конечных. При этом потомок генерируется так: 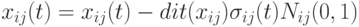 , где направление определяется выражением
, где направление определяется выражением 
- В работе [19] предложено использовать следующее выражение:
![\sigma_{ij}(t)=\left[\frac{1}{\sqrt{\beta_jf(x(t))+\lambda_j}}\right]\left[\frac{\lambda}{f_{\max}(t)-f_{\min}(t)}\right]](/sites/default/files/tex_cache/db4f6f6ca0bfd315ff71130a4586c8c7.png) , где
, где 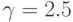 и
и 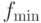 ,
, 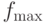 представляют минимальное и максимальное значения фитнесс-функции текущей популяции.
представляют минимальное и максимальное значения фитнесс-функции текущей популяции.
