Эволюционное программирование
10.7. Самоадаптация
мы видели ранее, самоадаптация используется не только в ЭП, но и ЭС и ГА. Первые методы самоадаптации в ЭП предложены Фогелем в [20], получившие развитие в последующих работах, которые можно разбить на три основные группы.
-
Аддитивные методы. Первый аддитивный метод предложен Фогелем [21], где
 и
и  - коэффициент обучения. В первых приложениях использовались значения
- коэффициент обучения. В первых приложениях использовались значения 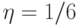 . Если
. Если  , то
, то 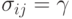 , где
, где  - малая положительная константа.
- малая положительная константа.Второй аддитивный метод [9] также предложен Фогелем, где
 , где
, где 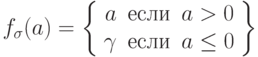 .
. 
-
Мультипликативные методы, где
 и
и 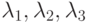 - управляющие параметры и
- управляющие параметры и  - максимальное количество итераций
- максимальное количество итераций
-
Методы на основе логарифмически нормального распределения [21],где
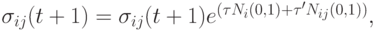
( 10.1) 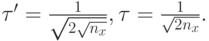
При этом потомок производится следующим образом:
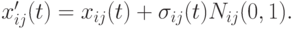
Эксперименты показали, что иногда имеет место стагнация вследствие слишком быстрой сходимости параметров. Вследствие этого отклонение становится слишком малым, что ограничивает возможности исследования пространства поиска.
-
Робастное ЭП предложено в [22], здесь представление каждой особи расширяется до вектора из
 параметров
параметров 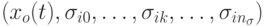 , где
, где 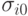 вектор параметров, получаемых в результате применения трех операторов мутации следующим образом:
вектор параметров, получаемых в результате применения трех операторов мутации следующим образом:
После выполнения приведенных операторов мутации порождается потомок путем использования выражения 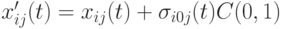 .
.
Аналогичным образом, Фогель [23] предложил векторную самоадаптацию, где на каждой итерации перед генерацией потомка вектор параметров с вероятностью 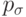 изменяется на один из оставшихся
изменяется на один из оставшихся 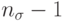 векторов. Здесь важно определить лучшие значения для
векторов. Здесь важно определить лучшие значения для  и
и 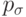 , которые являются проблемно- зависимыми.
, которые являются проблемно- зависимыми.
Отметим, что при самоадаптации в ЭП сначала генерируется потомок, а затем изменяются значения параметров. Это отличается от ЭС, где сначала изменяются значения параметров, а затем генерируются потомки. Порядок выполнения этих действий имеет существенное значение. Использование новых значений параметров в первом случае (ЭП) задерживается на одну итерацию.

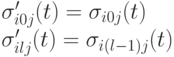
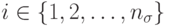 . Затем выполняется
. Затем выполняется  для
для 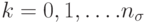 .
.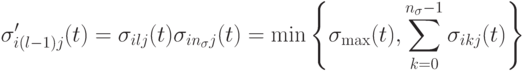
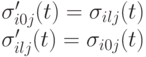
 и
и 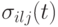 соответственно.
соответственно.