Игра Эренфойхта и понижение мощности
Лемма 4. Пусть 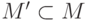 замкнуто относительно
сигнатурных функций и экзистенциально замкнуто. Тогда
замкнуто относительно
сигнатурных функций и экзистенциально замкнуто. Тогда  является элементарным расширением
является элементарным расширением 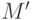 .
.
Отсюда уже вытекает утверждение теоремы 42: применим лемму 3 к
некоторому счетному подмножеству множества  , а затем
воспользуемся леммой 4.
, а затем
воспользуемся леммой 4.
Доказательство леммы 4 также довольно просто. Напомним определение элементарного расширения: требуется, чтобы

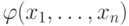 и для любых элементов
и для любых элементов 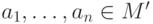 .
.(Формально следовало бы сказать: для любой формулы с параметрами
и любой оценки, при которой все параметры принимают значения в 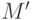 , истинность этой формулы в
, истинность этой формулы в 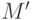 на этой оценке
равносильна истинности той же формулы в
на этой оценке
равносильна истинности той же формулы в  на той же оценке.)
на той же оценке.)
Будем доказывать это индукцией по построению формулы 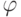 .
Для атомарных формул это очевидно: значения термов не
зависят от того, проводим ли мы вычисления в
.
Для атомарных формул это очевидно: значения термов не
зависят от того, проводим ли мы вычисления в  или
или 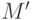 , а предикаты на
, а предикаты на 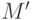 индуцированы из
индуцированы из  .
.
Если формула 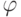 есть конъюнкция, дизъюнкция, импликация
или отрицание, то ее истинность как в
есть конъюнкция, дизъюнкция, импликация
или отрицание, то ее истинность как в  , так и в
, так и в 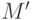 определяется истинностью ее частей (и можно сослаться на предположение индукции).
определяется истинностью ее частей (и можно сослаться на предположение индукции).
Единственный нетривиальный случай — если формула 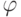 начинается с квантора. Мы можем сократить себе работу и
рассматривать только квантор существования, так как
начинается с квантора. Мы можем сократить себе работу и
рассматривать только квантор существования, так как 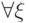 можно заменить на
можно заменить на 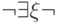 . Итак, пусть
. Итак, пусть 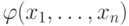 имеет вид
имеет вид
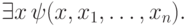
 для некоторых
для некоторых 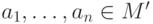 , то по определению истинности найдется
элемент
, то по определению истинности найдется
элемент 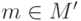 , для которого
, для которого 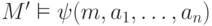 . Тогда по предположению индукции
(формула
. Тогда по предположению индукции
(формула 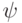 короче формулы
короче формулы 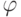 ) можно перейти к
большей интерпретации и заключить, что
) можно перейти к
большей интерпретации и заключить, что 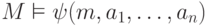 , и потому по определению
истинности
, и потому по определению
истинности 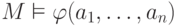 . Обратное
рассуждение просто так не проходит, поскольку существующий
элемент
. Обратное
рассуждение просто так не проходит, поскольку существующий
элемент  существует в
существует в  , а не в
, а не в 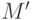 , и
предположение индукции применить нельзя. Однако ровно для этого у нас есть
требование экзистенциальной замкнутости, которое позволяет
заменить элемент
, и
предположение индукции применить нельзя. Однако ровно для этого у нас есть
требование экзистенциальной замкнутости, которое позволяет
заменить элемент  на другой элемент из
на другой элемент из 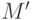 и
завершить доказательство.
и
завершить доказательство.Вот пример применения теоремы Левенгейма-Сколема в алгебре:
существует алгебраически замкнутое счетное подполе поля 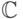 комплексных чисел. (В самом деле, требование алгебраической замкнутости
можно записать в виде счетной последовательности формул — по одной
для каждой степени многочлена. Аксиомы поля также можно записать
в виде формул. Значит, счетная элементарная подмодель
поля
комплексных чисел. (В самом деле, требование алгебраической замкнутости
можно записать в виде счетной последовательности формул — по одной
для каждой степени многочлена. Аксиомы поля также можно записать
в виде формул. Значит, счетная элементарная подмодель
поля 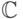 будет также алгебраически замкнутым полем.)
будет также алгебраически замкнутым полем.)
Впрочем, алгебраистов такое применение скорее насмешит — они и
так знают, что алгебраические элементы поля 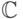 (корни
многочленов с целыми коэффициентами) образуют счетное
алгебраически замкнутое поле.
(корни
многочленов с целыми коэффициентами) образуют счетное
алгебраически замкнутое поле.
Любопытный парадокс связан с попытками применить теорему
Левенгейма-Сколема в теории множеств. Представим себе
интерпретацию языка теории множеств (предикаты  и
и 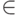 ), носителем которой является множество всех множеств. Такого
множества, строго говоря, не бывает, но если про это забыть и
применить теорему Левенгейма-Сколема об элементарной
подмодели, то можно оставить лишь счетное число множеств так,
чтобы истинность утверждений теории множеств не изменилась. Но
среди этих утверждений есть и утверждение о существовании
несчетного множества — как же так? Это рассуждение содержит
столько пробелов, что указать один из них совсем нетрудно. Тем
не менее оно может быть переведено в аксиоматическую теорию
множеств и дает интересные (хотя уже не парадоксальные)
результаты.
), носителем которой является множество всех множеств. Такого
множества, строго говоря, не бывает, но если про это забыть и
применить теорему Левенгейма-Сколема об элементарной
подмодели, то можно оставить лишь счетное число множеств так,
чтобы истинность утверждений теории множеств не изменилась. Но
среди этих утверждений есть и утверждение о существовании
несчетного множества — как же так? Это рассуждение содержит
столько пробелов, что указать один из них совсем нетрудно. Тем
не менее оно может быть переведено в аксиоматическую теорию
множеств и дает интересные (хотя уже не парадоксальные)
результаты.
Два дополнительных замечания усиливают теорему Левенгейма-Сколема.
Во-первых, легко видеть, что для всякого конечного
или счетного подмножества 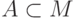 найдется счетная
элементарная подструктура
найдется счетная
элементарная подструктура  , содержащая все
элементы
, содержащая все
элементы  . (В самом деле, процесс замыкания, использованный
при доказательстве, можно начинать с множества
. (В самом деле, процесс замыкания, использованный
при доказательстве, можно начинать с множества  .)
.)
Во-вторых, можно отказаться от требования счетности сигнатуры
и сказать так: для всякого подмножества 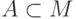 найдется
элементарная подструктура
найдется
элементарная подструктура 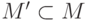 , содержащая
, содержащая  ,
мощность которой не превосходит максимума из
,
мощность которой не превосходит максимума из 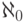 ,
мощности множества
,
мощности множества  и мощности сигнатуры. В самом деле, и
конструкция замыкания относительно сигнатурных операций, и
конструкция экзистенциального замыкания, и счетное объединение
возрастающей цепи не выводят мощность за пределы указанного
максимума, поскольку и формулы, и термы являются конечными
последовательностями символов сигнатуры и счетного числа других
символов (см. подробнее в [6]); то же самое
можно сказать о числе возможных наборов значений параметров.
и мощности сигнатуры. В самом деле, и
конструкция замыкания относительно сигнатурных операций, и
конструкция экзистенциального замыкания, и счетное объединение
возрастающей цепи не выводят мощность за пределы указанного
максимума, поскольку и формулы, и термы являются конечными
последовательностями символов сигнатуры и счетного числа других
символов (см. подробнее в [6]); то же самое
можно сказать о числе возможных наборов значений параметров.
Мы научились уменьшать мощность структуры, не меняя множества истинных в ней формул. Можно, напротив, увеличивать мощность (соответствующее утверждение иногда называют теоремой Левенгейма-Сколема об элементарном расширении). Но эта конструкция использует теорему компактности для языков первого порядка, которая в свою очередь вытекает из теоремы Геделя о полноте. Поэтому мы отложим обсуждение этого утверждения до следующей лекции.
