НОУ ИНТУИТ | Языки и исчисления. Лекция 8: Игра Эренфойхта и понижение мощности

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.04.2007 | Доступ: свободный | Студентов: 723 / 35 | Оценка: 4.60 / 4.30 | Длительность: 25:56:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

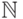85. Кто выигрывает в игре Эренфойхта для упорядоченных множеств (а) $\mathbb Z$ и $\mathbb R$ ; (б) $\mathbb R$ и $\mathbb Q$ ; (в) $\mathbb N$ и $\mathbb N+\mathbb Z$ ? Как он должен играть?

Приведенные примеры делают правдоподобной связь между наличием формулы, различающей интерпретации, и выигрышной стратегии для Н. При этом число ходов, которое понадобится Новатору, соответствует кванторной глубине различающей интерпретации формулы. Кванторная глубина формулы определяется так:

Глубина атомарных формул равна нулю.
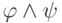Глубина формул $\varphi\vee\psi$ и $\varphi\wedge\psi$ равна максимуму глубин формул $\varphi$ и $\psi$ .
Глубина формулы $\neg\varphi$ равна глубине формулы $\varphi$ .
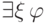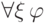Глубина формул $\exists\xi\,\varphi$ и $\forall\xi\,\varphi$ на единицу больше глубины формулы $\varphi$ .

Другими словами, глубина формулы — это наибольшая "глубина вложенности" кванторов (максимальная длина цепочки вложенных кванторов).

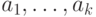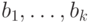Рассмотрим позицию, которая складывается в игре после ходов Н и К (перед очередным ходом Н ) и за ходов до конца игры (таким образом, общая длина игры есть k+l ). В этот момент в каждой из интерпретаций совместными усилиями Н и К выбрано по элементов. Пусть это будут элементы $a_1,\dots,a_k$ в одной интерпретации (назовем ее ) и $b_1,\dots,b_k$ в другой ( ).

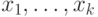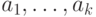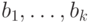Лемма. Если существует формула глубины с параметрами $x_1,\dots,x_k$ , отличающая $a_1,\dots,a_k$ от $b_1,\dots,b_k$ , то в указанной позиции Н имеет выигрышную стратегию; в противном случае ее имеет К.

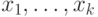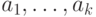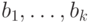Поясним смысл условия леммы. Пусть $\varphi$ — формула глубины , все параметры которой содержатся в списке $x_1,\dots,x_k$ . Тогда имеет смысл ставить вопрос о ее истинности в интерпретации при значениях параметров $a_1,\dots,a_k$ , а также в интерпретации при значениях параметров $b_1,\dots,b_k$ . 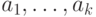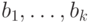Если окажется, что в одном случае формула $\varphi$ истинна, а в другом ложна, то мы говорим, что $\varphi$ отличает $a_1,\dots,a_k$ от $b_1,\dots,b_k$ .

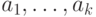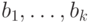Пусть такая формула $\varphi$ существует. Она представляет собой логическую (бескванторную) комбинацию некоторых формул вида $\forall \xi \,\psi$ и $\exists\xi \psi$ , где $\psi$ — формула глубины l-1 . Хотя бы одна из формул, входящих в эту комбинацию, должна также отличать $a_1,\dots,a_k$ от $b_1,\dots,b_k$ . Переходя к отрицанию, можно считать, что эта формула начинается с квантора существования. Пусть формула $\varphi$ , имеющая вид

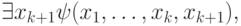
$\exists x_{k+1} \psi(x_1,\dots,x_k,x_{k+1}),$

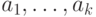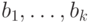истинна для $a_1,\dots,a_k$ и ложна для $b_1,\dots,b_k$ . Тогда найдется такое $a_{k+1}$ , для которого в

истинно

$\psi(a_1,\dots,a_k,a_{k+1}).$

Это $a_{k+1}$ и будет выигрывающим ходом Новатора; при любом ответном ходе $b_{k+1}$ Консерватора формула

$\psi(b_1,\dots,b_k,b_{k+1})$

будет ложной. Таким образом, некоторая формула глубины l-1

отличает $a_1,\dots,a_k,a_{k+1}$ от $b_1,\dots,b_k,b_{k+1}$ и потому, рассуждая по индукции, мы можем считать, что в оставшейся (l-1)

-ходовой игре Н имеет выигрышную стратегию. (В конце концов мы придем к ситуации, когда некоторая бескванторная формула отличает k+l

элементов в

от соответствующих элементов в

, то есть Н выиграет.)

Обратное рассуждение (если наборы не отличимы никакой формулой глубины , то К имеет выигрышную стратегию в оставшейся -ходовой игре) аналогично, но чуть более сложно. Здесь важно, что по существу есть лишь конечное число различных формул глубины .

Точнее говоря, будем называть две формулы (с параметрами) эквивалентными, если они одновременно истинны или ложны в любой интерпретации на любой оценке. Поскольку сигнатура конечна, существует лишь конечное число атомарных формул, все параметры которых содержатся среди $u_1,\dots,u_s$ . Существует лишь конечное число булевых функций с данным набором аргументов, поэтому существует лишь конечное число неэквивалентных бескванторных формул, все параметры которых содержатся среди $u_1,\dots,u_s$ . Отсюда следует, что существует лишь конечное число неэквивалентных формул вида

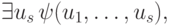
$\exists u_s\, \psi(u_1,\dots,u_{s}),$

и потому лишь конечное число неэквивалентных формул глубины

, параметры которых содержатся среди $u_1,\dots,u_{s-1}$ . (Здесь мы снова используем утверждение о конечности числа булевых функций с данным конечным списком аргументов, а также возможность переименовывать переменную под квантором, благодаря которой мы можем считать, что эта переменная есть u_s

.) Продолжая эти рассуждения, мы заключаем, что для любого

и для любого набора переменных $u_1,\dots,u_n$ существует лишь конечное число неэквивалентных формул глубины

, все параметры которых содержатся среди $u_1,\dots,u_n$ . (Здесь мы существенно используем конечность сигнатуры.)

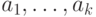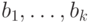Теперь можно закончить рассуждения про игру Эренфойхта. Пусть элементы $a_1,\dots,a_k$ нельзя отличить от элементов $b_1,\dots,b_k$ с помощью формул глубины . Опишем выигрышную стратегию для К. Пусть Н выбрал произвольный элемент в одной из интерпретаций, скажем, $a_{k+1}$ . Рассмотрим все формулы глубины l-1 с k+1 параметрами (с точностью до эквивалентности их конечное число); некоторые из них будут истинны на $a_1,\dots,a_{k+1}$ , а некоторые ложны. 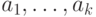Тогда формула, утверждающая существование $a_{k+1}$ с ровно такими свойствами (после квантора существования идет конъюнкция всех истинных формул и отрицаний всех ложных) будет формулой глубины , истинной на $a_1,\dots,a_k$ . 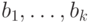По предположению эта формула должна быть истинной и на $b_1,\dots,b_k$ , и потому существует $b_{k+1}$ с теми же свойствами, что и $a_{k+1}$ . Этот элемент $b_{k+1}$ и должен пометить К. Теперь предположение индукции позволяет заключить, что в возникшей позиции (где до конца игры l-1 ходов) у К есть выигрышная стратегия.

Лемма доказана. Ее частным случаем является обещанный критерий элементарной эквивалентности:

Теорема 41. Интерпретации и элементарно эквивалентны тогда и только тогда, когда в соответствующей игре Эренфойхта выигрывает Консерватор.

86. Покажите, что условие конечности сигнатуры существенно (без него из элементарной эквивалентности не следует существование выигрышной стратегии для К ).

Заметим, что в некоторых случаях (например, для $\mathbb Z$ и $\mathbb Z+\mathbb Z$ ) игра Эренфойхта дает нам новый способ доказательства элементарной эквивалентности.

Дальше >>

Авторизоваться

Языки и исчисления

Игра Эренфойхта и понижение мощности

Вопросы и ответы