Выразимость в арифметике

Теорема 31. Пусть единичный квадрат разрезан на несколько меньших квадратов. Тогда все они имеют рациональные стороны.

Пусть дано такое разрезание с меньшими квадратами. Напишем формулу с параметрами ( из которых соответствуют размерам меньших квадратов, а — координатам их левых верхних углов), которая говорит, что эти параметры действительно задают разрезание квадрата (квадраты содержатся внутри единичного, не имеют общих точек и всякая точка единичного квадрата покрывается хотя бы одним из меньших квадратов). 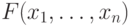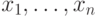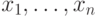Навесив кванторы существования по переменным, задающим координаты, получим формулу с параметрами , которая истинна, когда из квадратов размеров можно составить единичный квадрат.

Элиминация кванторов позволяет считать, что формула бескванторная, то есть представляет собой логическую комбинацию равенств и неравенств вида и с различными рациональными коэффициентами. Посмотрим на все выражения, стоящие в левой части таких равенств и неравенств. Подставим в них числа , соответствующие данному нам разрезанию. При этом получится истинная формула , в которой некоторые из левых частей равенств и неравенств будут равны нулю, а другие нет. Временно забудем про те, которые не равны нулю, а равные нулю будем воспринимать как левые части уравнений с неизвестными 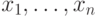(с нулем в правой части) независимо от того, входили ли они в как левые части уравнений или неравенств. Получится система уравнений, для которой числа будут решениями. Если эти числа являются единственными ее решениями, то они рациональны (например, потому, что правила Крамера для решения системы уравнений содержат отношения определителей с рациональными элементами). Покажем, что другого быть не может.

В самом деле, если решение не единственно, то есть целая прямая, проходящая через точку 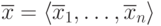и лежащая в множестве решений системы. Все точки прямой, достаточно близкие к , неотличимы от с точки зрения формулы и потому делают формулу истинной. В самом деле, левые части, равные нулю в , равны нулю на всей прямой, а левые части, отличные от нуля в точке , сохраняют знак в некоторой окрестности этой точки. Пусть — направляющий вектор этой прямой. Тогда при всех достаточно малых значениях из квадратов размеров

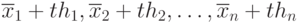
можно составить единичный квадрат. Но это невозможно. Чтобы убедиться в этом, достаточно оставить логику и вернуться к геометрии: площади этих квадратов в сумме должны равняться , но площадь каждого есть многочлен второй степени по , и коэффициент при положителен, поэтому сумма таких многочленов не может тождественно равняться единице ни на каком интервале.

Насколько существенна в этом рассуждении ссылка на возможность элиминации кванторов? В принципе можно было бы рассуждать так. Пусть дано разрезание квадрата. Посмотрим на конфигурацию, образуемую меньшими квадратами, и напишем равенства и неравенства на размеры частей, которые гарантируют, что в этой конфигурации нет щелей и перекрытий. (Далее продолжаем рассуждение как раньше.) Конечно, возникает вопрос: почему мы уверены, что такую систему уравнений и неравенств можно написать? Глядя на конкретную конфигурацию, это сделать легко, но как провести это рассуждение строго для общего случая, не вполне понятно.

Изложенные методы позволяют провести элиминацию кванторов и описать выразимые множества во многих ситуациях; несколько простых примеров такого рода предлагаются в качестве задач. Два более сложных примера (арифметика Пресбургера и теория сложения и умножения действительных чисел) разбираются в двух следующих разделах.

66. Описать выразимые предикаты, проведя элиминацию кванторов (и расширив сигнатуру, если нужно) для (а) 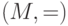, где — произвольное бесконечное множество; (б) ; (в) , где — операция прибавления единицы; (г) 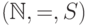, где — операция прибавления единицы; (д) , где — операция прибавления единицы, а — одноместный предикат "быть степенью двойки".