Схемы из функциональных элементов
Лемма. Пусть последовательность ![x_k\hm\in[0,1]](/sites/default/files/tex_cache/92890f21470c9f04a333edb98bc67df1.png) задана рекуррентной
формулой
задана рекуррентной
формулой 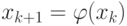 , где
, где
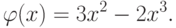
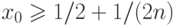 . Тогда
последовательность
. Тогда
последовательность  монотонно возрастает и приближается
к
монотонно возрастает и приближается
к  на расстояние
на расстояние 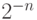 за
за  шагов. [Симметричное утверждение верно и при
шагов. [Симметричное утверждение верно и при 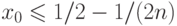 .]
.]Идея доказательства: посмотрим на функцию вблизи
точки 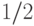 и у краев отрезка. В точке
и у краев отрезка. В точке 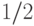 производная
больше
производная
больше  , поэтому удаление от
, поэтому удаление от 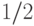 растет как геометрическая
прогрессия, и точка перейдет какую-то фиксированную границу
(например,
растет как геометрическая
прогрессия, и точка перейдет какую-то фиксированную границу
(например,  ) не позднее чем за
) не позднее чем за  шагов. Затем потребуется
шагов. Затем потребуется  шагов, чтобы дойти, скажем, до
шагов, чтобы дойти, скажем, до  . В единице первая производная функции равна нулю, поэтому
расстояние до единицы каждый раз примерно возводится в квадрат,
и потому для достижения погрешности
. В единице первая производная функции равна нулю, поэтому
расстояние до единицы каждый раз примерно возводится в квадрат,
и потому для достижения погрешности 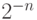 потребуется
потребуется  шагов (как в методе Ньютона отыскания корня). Всего
получается
шагов (как в методе Ньютона отыскания корня). Всего
получается  шагов, что и требовалось.
шагов, что и требовалось.
На самом деле справедливо гораздо более сильное утверждение:
существует схема размера 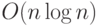 и глубины
и глубины  ,
состоящая только из элементов И и ИЛИ, которая имеет
,
состоящая только из элементов И и ИЛИ, которая имеет  входов
и
входов
и  выходов и осуществляет сортировку последовательности
выходов и осуществляет сортировку последовательности  нулей и единиц (это означает, что на выходе столько же
единиц, сколько на входе, причем выходная последовательность
всегда невозрастающая). Ясно, что средний бит выхода в такой
ситуации реализует функцию большинства.
нулей и единиц (это означает, что на выходе столько же
единиц, сколько на входе, причем выходная последовательность
всегда невозрастающая). Ясно, что средний бит выхода в такой
ситуации реализует функцию большинства.
При кажущейся простоте формулировки единственная известная конструкция такой схемы (сортирующая сеть AKS, придуманная Айтаи, Комлошом и Сцемереди сравнительно недавно, в 1983 году) весьма сложна, и появление какой-то более простой конструкции было бы замечательным достижением.
Многие нетривиальные результаты теории алгоритмов можно
переформулировать в терминах сложности каких-то булевых функций.
Например, есть вероятностный алгоритм проверки простоты большого
числа (применяемый в системах шифрования для проверки
простоты чисел из нескольких тысяч цифр). Используя
этот алгоритм, можно доказать такой факт: существует схема
проверки простоты  -битового числа (на вход подаются
-битового числа (на вход подаются  цифр, на выходе появляется единица, если число простое, и нуль,
если число составное), размер которой ограничен полиномом от
цифр, на выходе появляется единица, если число простое, и нуль,
если число составное), размер которой ограничен полиномом от  .
.
Вернемся к общим утверждениям о схемах и формулах. Мы уже говорили, что с точки зрения измерения размера схемы и формулы — это разные вещи (схемы экономичнее, так как в них одинаковые подформулы учитываются только один раз). Оказывается, что размер формулы можно связать с глубиной схемы.
Будем называть размером формулы число логических связок в
ней. Мы предполагаем, что формула использует конъюнкции,
дизъюнкции и отрицания, и в схемах будем использовать такие же
элементы. Напомним, что размером схемы мы называли число
элементов, а сложностью булевой функции — минимальный размер
схемы, ее вычисляющей. Сложность функции  обозначалась
обозначалась  (точнее
(точнее  , где
, где  —
набор разрешенных функциональных элементов, но сейчас мы договорились использовать
конъюнкции, дизъюнкции и отрицания и опускаем индекс
—
набор разрешенных функциональных элементов, но сейчас мы договорились использовать
конъюнкции, дизъюнкции и отрицания и опускаем индекс  ).
).
Минимальный размер формулы, выражающей функцию  , будем
обозначать
, будем
обозначать  . Очевидно,
. Очевидно, 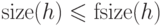 .
Более интересно, однако, следующее утверждение, связывающее
размер схемы с глубиной формулы. Обозначим через
.
Более интересно, однако, следующее утверждение, связывающее
размер схемы с глубиной формулы. Обозначим через  минимальную глубину схемы, вычисляющей функцию
минимальную глубину схемы, вычисляющей функцию  .
.
Теорема 16. Имеют место оценки 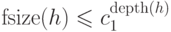 и
и 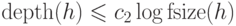 (для некоторых констант
(для некоторых констант 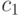 и
и 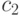 и для всех
и для всех  ). Другими
словами, меры сложности
). Другими
словами, меры сложности  и
и  отличаются не более
чем в константу раз.
отличаются не более
чем в константу раз.
Первая оценка очевидна: если мы скопируем повторяющиеся
фрагменты схемы, чтобы развернуть ее в дерево, то глубина не
изменится. Если она равна  , то в полученном дереве будет не
больше
, то в полученном дереве будет не
больше  элементов и соответствующая формула имеет размер
не более
элементов и соответствующая формула имеет размер
не более 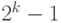 . (Напомним, что элементами являются
конъюнкции, дизъюнкции и отрицания, и потому ветвление не больше
. (Напомним, что элементами являются
конъюнкции, дизъюнкции и отрицания, и потому ветвление не больше  .)
.)
То же самое можно сказать индуктивно. Пусть глубина схемы равна  . Выход схемы является выходом некоторого элемента. Тогда на
его входы подаются булевы функции глубины не больше
. Выход схемы является выходом некоторого элемента. Тогда на
его входы подаются булевы функции глубины не больше  . По
предположению индукции их можно записать формулами размера
. По
предположению индукции их можно записать формулами размера 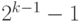 . Таких формул максимум две, так что общий размер не
превосходит
. Таких формул максимум две, так что общий размер не
превосходит 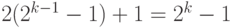 .
.
Вторая оценка сложнее. Если мы будем преобразовывать формулу в
схему естественным образом (введя вспомогательную переменную для
каждой подформулы), то глубина получившейся схемы может быть
близка к размеру формулы, а не к его логарифму. Например, если
формула имеет вид 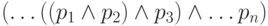 , то у нас получится цепочка элементов И, у которых каждый
следующий подвешен к левому входу предыдущего, и глубина равна
, то у нас получится цепочка элементов И, у которых каждый
следующий подвешен к левому входу предыдущего, и глубина равна 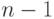 . Конечно, если использовать ассоциативность конъюнкции,
скобки можно переставить и получить более сбалансированное
дерево глубины примерно
. Конечно, если использовать ассоциативность конъюнкции,
скобки можно переставить и получить более сбалансированное
дерево глубины примерно  , как и требуется. Но как
выполнить такое преобразование в случае произвольной формулы?
, как и требуется. Но как
выполнить такое преобразование в случае произвольной формулы?
Обозначим данную нам формулу через  . Выберем у нее некоторую
подформулу
. Выберем у нее некоторую
подформулу  (как именно, мы объясним позже). Рассмотрим
формулу
(как именно, мы объясним позже). Рассмотрим
формулу 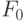 , которая получится, если вместо
, которая получится, если вместо  подставить
подставить  (ложь), а также формулу
(ложь), а также формулу 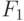 , которая получится, если
подставить
, которая получится, если
подставить  . Легко понять, что
. Легко понять, что  равносильна формуле
равносильна формуле 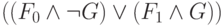 .
Если теперь удастся заменить формулы
.
Если теперь удастся заменить формулы 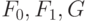 схемами
глубины не больше
схемами
глубины не больше  , то для
, то для  получится схема
глубины не больше
получится схема
глубины не больше  .
.
Такое преобразование полезно, если все три формулы 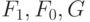 имеют заметно меньший размер, чем исходная формула
имеют заметно меньший размер, чем исходная формула  .
.
Лемма. У любой формулы размера  (при достаточно больших
(при достаточно больших  )
есть подформула размера от
)
есть подформула размера от 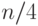 до
до 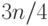 .
.
Доказательство. Каждая формула есть конъюнкция двух подформул,
дизъюнкция двух подформул или отрицание подформулы. Начав со всей
формулы, будем переходить к ее подформулам, на каждом шаге
выбирая из двух подформул наибольшую.
Тогда на каждом шаге размер убывает не более чем в два раза,
и потому мы не можем миновать
промежуток ![[n/4, 3n/4]](/sites/default/files/tex_cache/d6deb3b65c6e50a80978b57ced7084d1.png) , концы которого отличаются втрое. (На
самом деле тут есть небольшая неточность: размер формулы может
убывать чуть быстрее, чем вдвое, так как размер формулы на
единицу больше суммы размеров частей, но у нас есть запас,
поскольку концы промежутка отличаются втрое, а не вдвое.) Лемма доказана.
, концы которого отличаются втрое. (На
самом деле тут есть небольшая неточность: размер формулы может
убывать чуть быстрее, чем вдвое, так как размер формулы на
единицу больше суммы размеров частей, но у нас есть запас,
поскольку концы промежутка отличаются втрое, а не вдвое.) Лемма доказана.
Выбирая подформулу  с помощью этой леммы, мы гарантируем,
что размер всех трех формул
с помощью этой леммы, мы гарантируем,
что размер всех трех формул 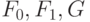 не превосходит
не превосходит 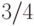 размера исходной формулы (подстановка нуля или единицы может
только уменьшить размер формулы — некоторые части можно будет выбросить).
размера исходной формулы (подстановка нуля или единицы может
только уменьшить размер формулы — некоторые части можно будет выбросить).
Применим ко всем трем формулам 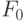 ,
, 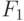 и
и  тот же прием, выделим в них подформулы среднего размера и так далее, пока мы
не спустимся до формул малого размера, которые можно записать в
виде схем как угодно. В итоге получится дерево с логарифмическим
числом уровней, на каждом из которых стоят схемы глубины
тот же прием, выделим в них подформулы среднего размера и так далее, пока мы
не спустимся до формул малого размера, которые можно записать в
виде схем как угодно. В итоге получится дерево с логарифмическим
числом уровней, на каждом из которых стоят схемы глубины  , а
в листьях находятся схемы глубины
, а
в листьях находятся схемы глубины  .
.
Другими словами, индукцией по размеру формулы, выражающей
некоторую функцию  , легко получить оценку
, легко получить оценку 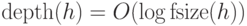 .
.
16. Определим глубину формулы как максимальное число вложенных
пар скобок; для единообразия будем окружать отрицание скобками
и писать 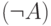 вместо
вместо 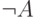 . Покажите, что при
этом не получится ничего нового: минимальная глубина формулы, записывающей
некоторую функцию
. Покажите, что при
этом не получится ничего нового: минимальная глубина формулы, записывающей
некоторую функцию  , совпадает с минимальной глубиной схемы,
вычисляющей
, совпадает с минимальной глубиной схемы,
вычисляющей  .
.
Определение формульной сложности  зависит от выбора
базиса. Оказывается, что здесь (в отличие от схемной сложности) выбор
базиса может изменить
зависит от выбора
базиса. Оказывается, что здесь (в отличие от схемной сложности) выбор
базиса может изменить  более чем в константу раз.
более чем в константу раз.
17. Объясните, почему доказательство теоремы 7 не переносится на случай формул.
Так происходит с функцией  (знак
(знак  обозначает сложение по модулю
обозначает сложение по модулю  ). Эта функция имеет формульную сложность
). Эта функция имеет формульную сложность  , если сложение по модулю
, если сложение по модулю  входит в базис. Однако в базисе И, ИЛИ,
НЕ она имеет большую сложность, как доказала Б.А.Субботовская.
Идея доказательства такова: если заменить случайно выбранную переменную в формуле с конъюнкциями и
дизъюнкциями на случайно выбранное значение
входит в базис. Однако в базисе И, ИЛИ,
НЕ она имеет большую сложность, как доказала Б.А.Субботовская.
Идея доказательства такова: если заменить случайно выбранную переменную в формуле с конъюнкциями и
дизъюнкциями на случайно выбранное значение  или
или  ,
то формула упростится (не только эта переменная пропадет, но с
некоторой вероятностью пропадут и другие). Если делать так
многократно, то от формулы останется небольшая часть — с другой
стороны, эта часть все равно должна реализовывать сложение
оставшихся аргументов по модулю
,
то формула упростится (не только эта переменная пропадет, но с
некоторой вероятностью пропадут и другие). Если делать так
многократно, то от формулы останется небольшая часть — с другой
стороны, эта часть все равно должна реализовывать сложение
оставшихся аргументов по модулю  .
.
18. Докажите, что функция большинства может быть вычислена не только схемой, но и формулой полиномиального размера, содержащей только связки И и ИЛИ.
19. Докажите, что значения  и
и  для
одной булевой функции
для
одной булевой функции  и различных полных базисов полиномиально
связаны: существует полином
и различных полных базисов полиномиально
связаны: существует полином  (зависящий от выбора базисов),
для которого
(зависящий от выбора базисов),
для которого 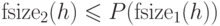 при всех
при всех  .
(Указание: использовать теорему 16.)
.
(Указание: использовать теорему 16.)
