Логика высказываний
Пример. Рассмотрим формулу 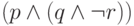 .
Она истинна в единственном случае — когда
.
Она истинна в единственном случае — когда  и
и  истинны, а
истинны, а  ложно (см.таблицу 1.3).
ложно (см.таблицу 1.3).
 |
 |
 |
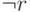 |
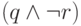 |
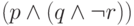 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 |
Некоторые формулы выражают логические законы — составные высказывания, истинные независимо от смысла их частей. Такие формулы (истинные при всех значениях входящих в них переменных) называют тавтологиями.
Пример. Формула 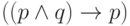 является
тавтологией (это можно проверить, например, составив таблицу).
Она выражает такой логический закон: из конъюнкции утверждений следует
первое из них.
является
тавтологией (это можно проверить, например, составив таблицу).
Она выражает такой логический закон: из конъюнкции утверждений следует
первое из них.
1. Как выглядит симметричное утверждение для дизъюнкции и какая формула его выражает?
Две формулы называют эквивалентными,если они истинны при
одних и тех же значениях переменных (другими словами, если они
задают одну и ту же булеву функцию). Например, формула 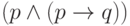 истинна лишь при
истинна лишь при 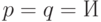 , и потому эквивалентна
формуле
, и потому эквивалентна
формуле 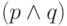 .
.
Рассмотрим формулу 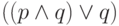 . Она истинна, если
переменная
. Она истинна, если
переменная  истинна, и ложна, если переменная
истинна, и ложна, если переменная  ложна. Хотелось бы сказать, что она эквивалентна
формуле
ложна. Хотелось бы сказать, что она эквивалентна
формуле  , но тут есть формальная трудность: она содержит
две переменные и потому задает функцию от двух аргументов
(типа
, но тут есть формальная трудность: она содержит
две переменные и потому задает функцию от двух аргументов
(типа 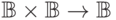 ), в то время как формула
), в то время как формула  задает
функцию одного аргумента. Мы не будем обращать на это внимания
и будем считать эти формулы эквивалентными. Вообще, если есть
список переменных
задает
функцию одного аргумента. Мы не будем обращать на это внимания
и будем считать эти формулы эквивалентными. Вообще, если есть
список переменных 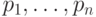 , содержащий все переменные
некоторой формулы
, содержащий все переменные
некоторой формулы  (и, возможно, еще какие-то
переменные), можно считать, что формула
(и, возможно, еще какие-то
переменные), можно считать, что формула  задает функцию от
задает функцию от  аргументов, возможно, на деле зависящую не от всех аргументов
(постоянную по некоторым аргументам)
аргументов, возможно, на деле зависящую не от всех аргументов
(постоянную по некоторым аргументам)
После сделанных оговорок легко проверить следующий факт: формулы  и
и  эквивалентны тогда и только тогда,
когда формула
эквивалентны тогда и только тогда,
когда формула 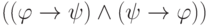 является
тавтологией. Используя сокращение
является
тавтологией. Используя сокращение  для
для 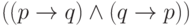 , можно записывать утверждения об
эквивалентности формул в виде тавтологий. Вот несколько таких эквивалентностей:
, можно записывать утверждения об
эквивалентности формул в виде тавтологий. Вот несколько таких эквивалентностей:
Теорема 1. Формулы





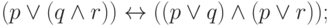
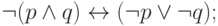
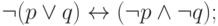
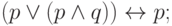
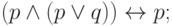
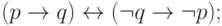
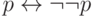
Первые четыре эквивалентности выражают коммутативность и ассоциативность конъюнкции и дизъюнкции. Проверим, например, вторую: левая и правая части истинны в единственном случае (когда все переменные истинны), и потому эквивалентны. (Для дизъюнкции удобнее смотреть, когда она ложна.)
Две следующие эквивалентности утверждают дистрибутивность—
заметим, что в отличие от сложения и умножения в кольцах здесь
верны оба свойства дистрибутивности. Проверить эквивалентность
легко, если отдельно рассмотреть случаи истинного и ложного  .
.
Следующие два свойства, законы Де Моргана, легко проверить, зная, что конъюнкция истинна, а дизъюнкция ложна лишь в одном случае. Эти свойства иногда выражают словами: "конъюнкция двойственна дизъюнкции".
Далее следуют два очевидных закона поглощения (один из них мы уже упоминали).
За ними идет правило контрапозиции, которое говорит, в
частности, что утверждения "если  совершенно, то
совершенно, то  четно"и "если
четно"и "если  нечетно, то
нечетно, то  несовершенно"равносильны. Хотя оно и очевидно проверяется с помощью таблиц
истинности, с ним связаны любопытные парадоксы. Вот один из них.
несовершенно"равносильны. Хотя оно и очевидно проверяется с помощью таблиц
истинности, с ним связаны любопытные парадоксы. Вот один из них.
Биолог А выдвинул гипотезу: все вороны черные. Проверяя ее, он вышел во двор и обнаружил на дереве ворону. Она оказалось черной. Биолог А радуется — гипотеза подтверждается. Биолог Б переформулировал гипотезу так: все не-черные предметы — не вороны (применив наше правило контрапозиции) и не стал выходить во двор, а открыл холодильник и нашел там оранжевый предмет. Он оказался апельсином, а не вороной. Биолог Б обрадовался — гипотеза подтверждается — и позвонил биологу А. Тот удивляется — у него тоже есть апельсин в холодильнике, но с его точки зрения никакого отношения к его гипотезе апельсин не имеет...
Другой парадокс: с точки зрения формальной логики утверждения "кто не с нами, тот против нас"и "кто не против нас, тот с нами"равносильны.
Последнее (и очевидное) правило 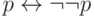 называется снятием двойного отрицания.
называется снятием двойного отрицания.
2. Перечисленные эквивалентности соответствуют равенствам для
множеств: например, первая гарантирует, что  для любых множеств
для любых множеств  и
и  . Какие утверждения
соответствуют остальным эквивалентностям?
. Какие утверждения
соответствуют остальным эквивалентностям?
3. Две формулы, содержащие только переменные и связки 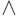 ,
, 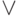 и
и 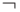 , эквивалентны. Докажите, что они
останутся эквивалентными, если всюду заменить
, эквивалентны. Докажите, что они
останутся эквивалентными, если всюду заменить 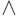 на
на 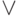 и
наоборот.
и
наоборот.
Далеко не все тавтологии имеют ясный интуитивный
смысл. Например, формула  является
тавтологией (если одно из утверждений
является
тавтологией (если одно из утверждений  и
и  ложно,
то из него следует все, что угодно; если оба истинны, то тем более
формула истинна), хотя и отчасти противоречит нашей интуиции —
почему, собственно, из двух никак не связанных утверждений одно
влечет другое? Еще более загадочна тавтология
ложно,
то из него следует все, что угодно; если оба истинны, то тем более
формула истинна), хотя и отчасти противоречит нашей интуиции —
почему, собственно, из двух никак не связанных утверждений одно
влечет другое? Еще более загадочна тавтология
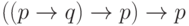
Отступление о пользе скобок.На самом деле наше определение истинности содержит серьезный
пробел. Чтобы обнаружить его, зададим себе вопрос: зачем нужны
скобки в формулах? Представим себе, что мы изменим определение
формулы, и будем говорить, что 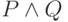 и
и  являются формулами для любых
являются формулами для любых  и
и  . Останутся ли наши
рассуждения в силе?
. Останутся ли наши
рассуждения в силе?
Легко понять, что мы столкнемся с трудностью при определении
булевой функции, соответствующей формуле. В этом определении
мы подставляли нули и единицы на место переменных и затем
вычисляли значение формулы с помощью таблиц истинности для
связок. Но теперь, когда мы изменили определение формулы,
формула 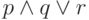 может быть получена двумя способами —
из формул
может быть получена двумя способами —
из формул 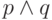 и
и  с помощью операции
с помощью операции 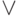 и из формул
и из формул  и
и 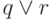 спомощью операции
спомощью операции 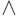 . Эти два толкования дадут разный результат при попытке вычислить
значение
. Эти два толкования дадут разный результат при попытке вычислить
значение 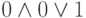 .
.
Из сказанного ясно, что скобки нужны, чтобы гарантировать однозначность синтаксического разбора формулы. Точнее говоря, верно такое утверждение:
Теорема 2 (однозначность разбора). Пропозициональная формула, не являющаяся переменной,
может быть представлена ровно в одном из четырех видов  ,
, 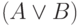 ,
,  или
или 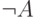 , где
, где  и
и  — некоторые
формулы, причем
— некоторые
формулы, причем  и
и  (в первых трех случаях) восстанавливаются однозначно.
(в первых трех случаях) восстанавливаются однозначно.
Формальное доказательство можно провести так: назовем скобочным итогом разницу между числом открывающихся и закрывающихся скобок. Индукцией по построению формулы легко доказать такую лемму:
Лемма. Скобочный итог формулы равен нулю. Скобочный итог любого начала формулы неотрицателен и равен нулю, лишь если это начало совпадает со всей формулой, пусто или состоит из одних символов отрицания.
Слова "индукцией по построению"означают, что мы
проверяем утверждение для переменных, а также
доказываем, что если оно верно для формул  и
и  , то
оно верно и для формул
, то
оно верно и для формул  ,
, 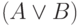 ,
,  и
и 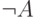 .
.
После того как лемма доказана, разбор формулы проводится так: если она начинается с отрицания, то может быть образована лишь по третьему правилу. Если же она начинается со скобки, то надо скобку удалить, а потом искать непустое начало, имеющее нулевой скобочный итог и не оканчивающееся на знак логической операции. Такое начало единственно (как легко проверить, используя лемму). Это начало и будет первой частью формулы. Тем самым формула разбирается однозначно.
Нет смысла вдаваться в подробности этого (несложного) рассуждения: вообще-то алгоритмы разбора формул — это отдельная большая и практически важная тема (в первую очередь в связи с компиляторами). Приведенный нами алгоритм далеко не оптимален. С другой стороны, мы вообще можем обойти эту проблему, потребовав, чтобы при записи формул левая и правая скобки, окружающие формулу, связывались линией — тогда однозначность разбора формулы не вызывает вопросов, и больше ничего нам не надо.
В дальнейшем мы будем опускать скобки, если они либо не играют роли (например, можно написать конъюнкцию трех членов, не указывая порядок действий в силу ассоциативности), либо ясны из контекста.
4. Польский логик Лукасевич предлагал обходиться без скобок,
записывая в формулах сначала знак операции, а потом операнды
(без пробелов и разделителей). Например, 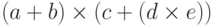 в его обозначениях запишется как
в его обозначениях запишется как 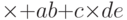 . Эту запись еще называют польской записью. Обратная
польская запись отличается от нее тем, что знак операции идет
после операндов. Покажите, что в обоих случаях порядок действий
восстанавливается однозначно.
. Эту запись еще называют польской записью. Обратная
польская запись отличается от нее тем, что знак операции идет
после операндов. Покажите, что в обоих случаях порядок действий
восстанавливается однозначно.
