Синхронизация времени в распределенном имитационном моделировании
В предыдущей лекции мы рассмотрели такие вопросы, как управление временем в распределенных вычислениях, управление временем в последовательном имитационном моделировании. Рассмотрим, какие механизмы существуют для синхронизации логических процессов распределенной имитационной модели.
Управление временем в распределенном моделировании
Управление временем в распределённом моделировании должно обеспечивать выполнение событий в правильном хронологическом порядке. Более того, на алгоритмы синхронизации возлагается обязанность корректно выполнять повторные имитационные прогоны. При повторном моделировании пользователь должен быть уверен, что он получит те же результаты, что и в первый раз, если входные данные останутся неизменными. Обеспечение следования событий в правильном порядке и проблемы повторного имитационного прогона для моделирования тренажёров несущественно. Поэтому речь о дискретно-событийном моделировании.
Сделаем предположение, что имитационная модель представляет собой совокупность логических процессов ( LPi ), которые взаимодействуют друг с другом, посылая друг другу сообщения с временной меткой (time stamped) или события. Логические процессы являются отражением физических процессов PPj. События логического процесса должны выполняться в хронологическом порядке. Это требование называют ограничением локальной каузальности (local causality constraint). Можно показать, что если игнорировать события с одинаковыми временными метками и если процесс поддерживает ограничение локальной каузальности, то выполнение имитационной программы на параллельном компьютере даст такие же результаты, как и выполнение на последовательном, где все события выполняются в соответствии с их временными метками. Кроме того, это свойство позволяет убедиться в том, что выполнение имитационного прогона повторяемо (даёт те же результаты при одном и том же наборе исходных данных).
Будем рассматривать каждый логический процесс как последовательный симулятор, поддерживающий дискретное событийное моделирование. А это означает, что каждый логический процесс содержит локальную информацию о состоянии объектов моделирования и список событий, которые были запланированы для этого процесса, но ещё не были выполнены (pending event list). Этот список необработанных событий включает локальные события (т.е. запланированные самим процессом LPi ) и события, запланированные для него другими процессами.
Работа симулятора заключается в том, чтобы выбрать из списка необработанных событий событие с минимальной временной меткой и обработать его. Так выполнение процесса можно рассматривать как выполнение последовательности событий. Выполнение событие сопровождается изменением переменных, которые определяют состояние моделируемого объекта. Кроме того, логический процесс при выполнении очередного события может запланировать выполнение нового события ej для самого себя или для другого логического процесса. Каждый логический процесс имеет локальные часы. Локальные часы указывают на время выполнения самого последнего обработанного симулятором события. Время, на которое запланировано логическим процессом любое событие должно быть больше, чем значение его локальных часов.
Итак, m = {LP, ME}, где LP – это множество процессов, ME – коммуникационная среда для передачи сообщений от одного процесса другому. В свою очередь,
LPi = {Q, E, Sch, Ch, T}, где
T – линейно-упорядоченное абстрактное множество с отношением порядка <. Множество T называют множеством моментов времени.
Ein – это множество внутренних событий процесса.
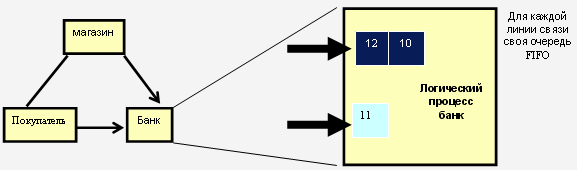
Em –множество событий, полученных процессом i процессом от j -того процесса. Если процесс LPi получит сообщение (событие, которое запланировано для него процессом LPj ), то он должен переупорядочить очередь локальных событий (или календарь событий) C = ((e1, t1), (e2 , t2),…,(en , tn)), включив в неё пару (ej , tj). Очередь С упорядочена по возрастанию временных меток событий.
Sch – преобразование планирования событий процесса ei, Sch: E x Q x T -> E ;
Ch – преобразование изменения состояния Сh: E x Q x T -> Q,
Tloc – локальное время логического процесса (время последнего обработанного события из множества E ).
Текущее модельное время 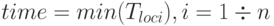 .
.
Парадоксы времени
Алгоритм управления временем должен следить за тем, чтобы события выполнялись в хронологическом порядке. Эта задача не является тривиальной. Действительно, логический процесс заранее не может знать о том, на какое время будет запланировано событие, которое он получает от другого логического процесса. Пусть в списке необработанных событий хранится событие с временной меткой 10. Может ли симулятор логического процесса выбрать его для обработки. Это можно было бы сделать, если бы логический процесс каким-нибудь образом знал о том, что другой логический процесс не запланировал для него события, со временем меньшим, чем 10.
Рассмотрим другой пример.
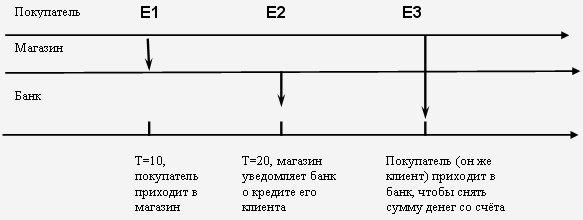
Пусть модель представляет собой совокупность трёх процессов. Один процесс отображает поведение покупателя, второй – магазина, в котором покупатель совершает покупки, а третий процесс – деятельность банка, со счёта которого покупатель снимает деньги.
Предположим, что покупатель приобрёл товары в магазине на определённую сумму N (в кредит) (событие e1, произошло в момент времени t1 = 9 ). Магазин уведомил об этом банк ( e2, t2 = 10 ) Сумма на счёте уменьшается: S = S – N. Покупатель посещает банк с целью снять деньги со счёта ( e3, t3=11 ). Если денег на счёте достаточно, то банк выдаёт клиенту (которым является покупатель) запрошенную им сумму. Если счёт меньше запрошенной суммы, то покупателю будет отказано.
Хронологический порядок событий: e1, e2, e3 (рис. 8.1).
Рассмотрим описанную выше ситуацию: если уведомление в банк из магазина поступит позже того, как покупатель снимет сумму с вклада в банке (которой уже нет на счёте), то банк понесёт убытки. Ситуация, которая обрисована выше, возникла вследствие того, что хронология событий была нарушена (рис. 8.2).
Нарушение хронологического порядка могло произойти по той причине, что в распределённом моделировании время для разных логических процессов движется с разной скоростью. Например, если процесс, реализующий работу магазина, выполняется на загруженном процессоре, то уведомление банку поступает позже, поскольку процесс банк "убежал" вперёд (он выполняется на менее загруженном процессоре).
Распределённый алгоритм должен уметь бороться с такими парадоксами времени.
В этом и заключается проблема синхронизации компонентов распределённого моделирования. Было предпринято множество попыток решить эту проблему. В настоящее время все алгоритмы синхронизации делятся на консервативные и оптимистические.
Если мы вернёмся к примеру 1, то консервативный алгоритм не позволит логическому процессу обрабатывать событие с временной отметкой 10, пока не убедится, что другой логический процесс не запланировал для него события с временной меткой, меньшей 10.
Оптимистический алгоритм позволяет выбирать из списка необработанных событий очередное событие и обрабатывать его, исключив проверку событий, планируемых другими логическими процессами. Однако отдельный программный механизм реализует обнаружение ошибок и восстановление от ошибок выполнения событий, которые происходят не в хронологическом порядке.
Рассмотрим более подробно каждый из алгоритмов управления временем.
Консервативное управление временем
Первые алгоритмы синхронизации использовали консервативный подход. Принципиальная задача консервативного протокола – определить время, когда обработка очередного события из списка необработанных событий является "безопасным". Иными словами, событие является безопасным, если можно гарантировать, что процесс в дальнейшем не получит от других процессов событие с меньшей временной меткой. Консервативный подход не позволяет выполнять событие до тех пор, пока нет гарантии, что оно является безопасным.
Большинства консервативных алгоритмов основано на вычислении LBTS (Lower Bound on the Time Stamp – нижняя граница временных меток) будущих сообщений, которые могут быть получены логическим процессом. Этот механизм позволяет определить, является ли очередной событие из списка необработанных событий безопасным. Действительно, если консервативный алгоритм определит, что LBTS = 11, то все события из списка необработанных событий с временной отметкой, меньшей 11, являются безопасными и могут быть выполнены. Соответственно, события с временной меткой, большей 11 не являются безопасными и не могут быть выполнены. Что касается событий, которые имеют временную отметку, равную 12 ( LBTS = 12 ), то их обработка зависит от реализации конкретного консервативного алгоритма и правил, по которому должны обрабатываться события, запланированные на один и тот же момент времени (одновременные события – simultaneous events).
Будем считать, что логические процессы не содержат событий, запланированных на одно и то же модельное время.

 .
.