Алгоритмы обхода сайтов
Алгоритмом обхода называется алгоритм, обладающий следующими тремя свойствами.
- В каждом вычислении один сайт-инициатор, который начинает выполнение алгоритма, посылая ровно одно сообщение.
- Процесс сайта, получая сообщение, либо посылает одно сообщение дальше, либо выполняет процедуру return(OK).
- Алгоритм завершается в инициаторе и к тому времени, когда это происходит, процесс каждого сайта посылает сообщение хотя бы один раз.
Из первых двух свойств следует, что в каждом конечном вычислении решение принимает ровно один процесс. Говорят, что алгоритм завершается в этом процессе.
В каждой достижимой конфигурации алгоритма обхода либо передается ровно одно сообщение, либо ровно один процесс получил сообщение и еще не послал ответное сообщение. С более абстрактной точки зрения, сообщения в вычислении, взятые вместе, можно рассматривать как единый объект (маркер), который передается от процесса к процессу и, таким образом, "посещает" все процессы. В следующей лекции алгоритмы обхода используются для построения алгоритмов выбора и для этого важно знать не только общее количество переходов маркера в одной волне, но и сколько переходов необходимо для того, чтобы посетить первые k процессов.
Алгоритм обхода полного графа
Полный граф содержит все возможные связи между вершинами. Пусть n – количество узлов в полном графе. По отношению к данному узлу this – инициатору обозначим множество остальных вершин полного графа: {u1, u2, .., un – 1}.
Полный граф можно обойти путем последовательного опроса. Алгоритм подобен соответствующему алгоритму из предыдущей лекции, но за один раз опрашивается только один сосед инициатора. Только когда получен ответ от одного соседа, опрашивается следующий. Таким образом, сообщение с номером (2i – 1) – это опрос для сайта ui, а сообщение с номером 2i – ответ этого сайта. Всего же за время исполнения происходит обмен 2(i – 1) сообщениями.
Алгоритм последовательного опроса:
Процесс сайта – инициатора:
var i: integer init 0 ; (* счетчик *)
Для инициатора:
begin while i < n – 1 do
begin out token to ui+1 ;
receive token; i := i + 1
end ;
return(OK)
endПроцесс сайта не-инициатора:
begin receive token from u ; out token to u end
Алгоритм обхода тора
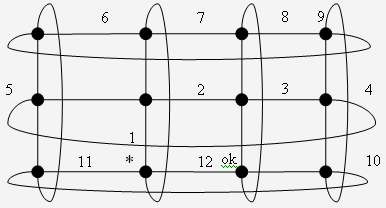
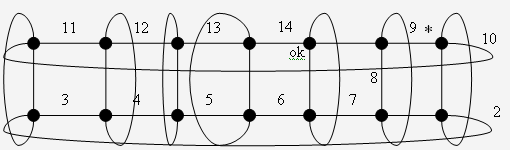
Граф вида "тор" представляет собой решетку с дополнительными ребрами, соединяющими вершины из верхнего ряда ("строки") решетки с вершинами из нижнего ряда, а также с ребрами, соединяющими вершины из левого ряда ("столбца") решетки с вершинами из правого ряда. Таким образом, возникают дополнительные циклы. Каждая вершина тора (в отличие от решетки) имеет степень 4, т.е. граф является регулярным. При стандартном изображении такого графа каждая вершина имеет "левого" соседа, "правого" соседа, "верхнего" соседа, "нижнего" соседа (рис. 17.1). Тор, построенный на основе решетки m x n, содержит mn узлов и 2mn ребер. Количество ребер можно подсчитать как непосредственно, так и на основе известной теоремы теории графов: "сумма степеней узлов равна удвоенному числу ребер".
Из-за его регулярных свойств тор или его модификации часто используются в различных архитектурах. Например, одна из первых архитектур многопроцессорных ЭВМ ILLIAC-IV использовала тороподобное соединение процессоров.
Требуется обойти все узлы тора m x n (но не все ребра). Инициатором – начальным узлом при обходе может быть любой из узлов. Алгоритм ориентирован на топологию тора, но на сайтах нет глобальной информации о топологии, имеются лишь имена ребер ( L, R, U, D ), определяющие направления в соответствии с приведенным выше рисунком. Их можно считать локальным знанием о топологии.
Действия инициатора (выполняется один раз):
out (token, 1) through U
Действия процесса каждого сайта при получении маркера (token, k):
begin if k = m*n then return(OK)
else if (k mod n = 0) then out (token, k+1) through U
else out (token, k+1) through R
endНа рис. 17.2 и 17.3 показан порядок обхода торов 3 x 4 и 2 x 5. Звездочкой обозначен сайт – инициатор обхода, а буквами "ОК" – сайт, сообщающий о завершении обхода. Около ребра записано число – значение k, которое передается по этому ребру от одного сайта к другому.
Алгоритм обхода гиперкуба
В теории графов известен класс графов Qn , называемых кубами размерности n, или гиперкубами. Это семейство описывается формулами Qn = K2 x Qn – 1 , Q1 = K2 . Здесь K2 – полный граф с двумя вершинами, т.е. две вершины, соединенные одним ребром. Операция n - перемножение графов.
Эта операция для графов A и B определяется следующим образом.
Результатом операции является граф C = A x B, множество вершин которого состоит во взаимнооднозначном отношении с декартовым произведением множеств вершин графов A и B, V(C) = V(A) x V(B).
Множество ребер E(C) графа C порождается множествами ребер E(A) и E(B). Пусть вершина  соответствует паре вершин (a1 , b1),
соответствует паре вершин (a1 , b1),  ,
, 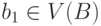 , а вершина
, а вершина  соответствует паре вершин (a2 , b2),
соответствует паре вершин (a2 , b2),  ,
, 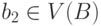 , тогда v1 смежна v2 (между ними имеется ребро), если выполняется одно из двух условий:
, тогда v1 смежна v2 (между ними имеется ребро), если выполняется одно из двух условий:
- a1 = a2 и b1 смежна b2 ;
- b1 = b2 и a1 смежна a2 ;
Гиперкуб Q1 = K2 , т.е. представляет собой "отрезок" с точки зрения изображения геометрических фигур. Он содержит 2 вершины. Степень каждой из них равна единице. Гиперкуб Q2 с точки зрения теории графов представляет собой цикл из четырех вершин, в геометрическом представлении – квадрат. Степень каждой вершины равна 2. Гиперкуб Q3 может быть представлен вершинами и ребрами геометрической фигуры – куба. Этот гиперкуб содержит 8 вершин степени 3.
В общем случае гиперкуб Qn содержит 2n вершин степени n. В связи с этим удобно кодировать вершины строками из n бит – двоичной формой номеров вершин: от 000…0 до 111…1. Левый разряд числа (символ строки) будем называть нулевым разрядом, правый – (n – 1) -м. Тогда две вершины смежны в гиперкубе, если их коды отличаются в точности одним битом. Например, смежными с вершиной с кодом 010 будут вершины с кодами 110, 000, 011.
В каждом узле u инцидентные ему ребра можно перенумеровать числами от 0 до n – 1 так, что ребро номер 0 будет соединять узел u с таким узлом гиперкуба, код которого отличается от кода u в нулевом разряде. Соответственно, ребро номер 1 идет к вершине с отличием в коде в первом разряде и т.д.
Действия в алгоритме для гиперкуба.
Для инициатора (выполняется один раз):
out (token, 1) through канал n – 1
Для каждого процесса при получении маркера (token, k):
begin if k=2n then return(OK)
else begin пусть l - наибольший номер, такой, что 2l|k;
out (token, k+1) through канал l
end
endИз алгоритма видно, что решение принимается после 2n пересылок маркера. Пусть p0 – инициатор, а pk – процесс, который получает маркер (token, k). Для любого k < 2n, обозначения pk и pk+1 отличаются на 1 бит, индекс которого обозначим как l(k), удовлетворяющий следующему условию:

Т.к. для любого i < n существует равное количество 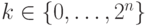 с l(k) = i, то p0 = p2^n и решение принимается в инициаторе. Можно показать, что из pa = pb следует, что 2n|(b – a), откуда следует, что все p0, ..., p2^n-1 различны.
с l(k) = i, то p0 = p2^n и решение принимается в инициаторе. Можно показать, что из pa = pb следует, что 2n|(b – a), откуда следует, что все p0, ..., p2^n-1 различны.
Алгоритм Тарри
Алгоритм обхода для произвольных связных графов был дан Тарри. Алгоритм основан на следующих двух правилах.
- Процесс никогда не передает маркер дважды по одному и тому же каналу.
- Не-инициатор передает маркер своему предшественнику (соседу, от которого он впервые получил маркер), только если невозможна передача по другим каналам, в соответствии с правилом 1.
В следующем тексте используются локальные переменные сайтов:
pre – сайт, предшествующий тому, который выполняет текущий процесс, т.е. сайт, с которого пришел маркер;
used[q] – признак того, отправлен ли был маркер на сайт u.
![var \ used[q]: boolean \ init \ false \ для \ всех \ u \in Out(this);
\\
pre : site \ init \ udef ;](/sites/default/files/tex_cache/b6e7ed0894c7e34be7d200bb203aa2e9.png)
Для инициатора (выполняется один раз):
![begin \ pre := this ; \ выбор \ u \in Out(this);
\\
used[u] := true ; \ out \ token \ to \ u ;
\\
end](/sites/default/files/tex_cache/696401d9e2f08d6734c905c1e73d58a4.png)
Для каждого процесса при получении token от s:
![begin \ \ \ if \ pre = udef \ then \ pre := s;
\\
if \ \forall u \in Out(this) : used[u]
\\
then \ return(OK)
\\
else \ if \ \exists u \in Out(this): (u \ne pre \& \neg used[u])
\\
then \ begin \ выбор \ u \in Out(this) \setminus \{ pre\} с \neg used[u] ;
\\
used[u] := true ; \ out \ token \ to \ u
\\
end
\\
else \ begin \ used[pre] := true ;
\\
out \ token \ to \ pre
\\
end
\\
end](/sites/default/files/tex_cache/6b73b1193cbfffeb2b20228222ae9df1.png)
Так как процесс каждого сайта передает маркер через каждый канал не более одного раза, то каждый процесс получает маркер через каждый канал не более одного раза. Каждый раз, когда маркер захватывается не-инициатором u, получается, что процесс u получил маркер на один раз больше, чем послал его. Отсюда следует, что количество каналов, инцидентных u, превышает количество каналов, использованных u, по крайней мере, на 1. Таким образом, u не завершает процесс, а передает маркер дальше. Следовательно, завершение процесса производится в сайте-инициаторе.
Ниже показывается, что когда алгоритм завершается, каждый процесс передал маркер.
- Все каналы, инцидентные инициатору, были пройдены один раз в обоих направлениях. Инициатором маркер был послан по всем каналам, иначе алгоритм не завершился бы. Инициатор получил маркер ровно столько же раз, сколько отправил его; так как инициатор получал маркер каждый раз через другой канал, то маркер пересылался через каждый канал по одному разу.
- Для каждого посещаемого процесса u все каналы, инцидентные u были пройдены один раз в каждом направлении. Предположив, что это не так, выберем в качестве u первый встретившийся процесс, для которого это не выполняется, и заметим, что из пункта (1) u не является инициатором. Из выбора u, все каналы, инцидентные pre(u) были пройдены один раз в обоих направлениях, откуда следует, что u переслал маркер своему предшественнику. Следовательно, u использовал все инцидентные каналы, чтобы переслать маркер; но, так как маркер в конце остается в инициаторе, u получил маркер ровно столько же раз, сколько отправил его, т.е. u получил маркер по одному разу через каждый инцидентный канал. Мы пришли к противоречию.
- Все процессы были посещены и каждый канал был пройден по одному разу в обоих направлениях. Если есть непосещенные процессы, то существуют соседи u и s такие, что u был посещен, а s не был. Это противоречит тому, что все каналы u были пройдены в обоих направлениях. Следовательно, из пункта (2), все процессы были посещены и все каналы пройдены один раз в обоих направлениях.
Каждое вычисление алгоритма Тарри определяет остовное дерево графа. В корне дерева находится инициатор, а каждый не-инициатор u в конце вычисления занес своего предшественника в дереве в переменную pre.