Волновые алгоритмы распространения информации
Многие задачи в распределенных системах решаются путем пересылки сообщений согласно некоторой схемы, которая гарантирует участие всех сайтов. Эта схема зависит от топологических особенностей системы, т.е. от вида графов, представляющих связи между узлами – сайтами.
Распределенные алгоритмы обычно допускают большой набор возможных трасс вычислений благодаря недетерминированности как в процессах, так и в подсистеме передачи. Трасса вычисления – это набор событий, частично упорядоченных отношением причинно-следственного предшествования. Волновой алгоритм обменивается конечным числом сообщений со всеми сайтами и затем на основе этого выполняет специальную процедуру return(OK).
Волновой алгоритм - это распределенный алгоритм, который удовлетворяет следующим трем требованиям:
- Конечность. Каждое вычисление содержит конечное число событий.
- Успешное завершение. Каждое вычисление содержит хотя бы одно событие return(OK).
- Зависимость. В каждом вычислении каждому событию вызова процедуры return(OK) предшествует (в смысле причинно-следственной связи) какое-либо событие на каждом сайте.
Выполнение волнового алгоритма называется волной. Кроме того, в выполнении алгоритма различаются сайты инициаторы и сайты не-инициаторы. Сайт является инициатором, если он начинает выполнение своего локального алгоритма самопроизвольно, т.е. при выполнении некоторого условия, внутреннего по отношению к процессу. Не-инициатор включается в алгоритм только когда прибывает сообщение и вызывает выполнение локального алгоритма сайта. Начальное событие инициатора – внутреннее событие или событие посылки сообщения, начальное событие не-инициатора – событие получения сообщения.
Обычно при применении волновых алгоритмов в сообщение могут быть включены дополнительные переменные и другая информация. Многие приложения используют одновременное или последовательное распространение нескольких волн; в этом случае в сообщение должна быть включена информация о волне, которой оно принадлежит. Кроме того, процесс может хранить дополнительные переменные для управления волной, или волнами, в которых он в настоящее время активен.
Алгоритм для кольцевой архитектуры
Если сайты распределенной системы соединены однонаправленными каналами связи так, что образуют граф – ориентированный цикл, применим следующий волновой алгоритм.
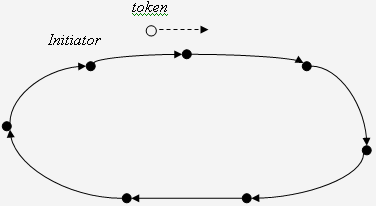
Суть его в следующем. Один из сайтов – инициатор посылает маркер token своему единственному соседу по выходу (в ориентированном цикле каждый сайт имеет в точности один вход и один выход; выход одного сайта соединен с входом соседнего). Маркер, как правило, не имеет "содержания". Важен лишь факт отсылки маркера или поступления маркера.
Любой сайт (кроме инициатора), получив маркер, тут же отправляет его соседу. Инициатор, получив маркер, завершает процесс. Завершение процесса заключается в том, что сайт не посылает далее маркер, а выполняет некоторую процедуру return(OK) – успешный возврат. Рис. иллюстрирует работу этого алгоритма.
Опишем волновой алгоритм для кольцевой архитектуры, используя языковые средства из "Моделирование распределенных систем. Язык Triad" .
Структура распределенной системы задается формулой
System := dcycle(n)(Node[1..n]).
В системе имеется n сайтов с именами Node[i]. У каждого сайта имеется один входной полюс и один выходной полюс. Выходной полюс сайта Node[i], 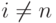 , соединен каналом связи с входным полюсом сайта Node[i + 1]. Выходной полюс сайта Node[n] соединен с входным полюсом сайта Node[1].
, соединен каналом связи с входным полюсом сайта Node[i + 1]. Выходной полюс сайта Node[n] соединен с входным полюсом сайта Node[1].
Алгоритм (рутина) узла – инициатора: routine Initiator initial out token; endi event; if message = token then return(OK) ende endrout.
Здесь идентификатор message обозначает пришедшее на вход рутины сообщение. Этот идентификатор не описывается, он является системной переменной без определенного типа. Реально пришедшее на вход сообщение, "скрывающееся" за этим идентификатором, тип может иметь (кроме абстрактных сообщений). Поэтому в операциях сравнения сначала сравниваются (динамически) типы левой и правой частей, а при совпадении типов – значения.
Рутины остальных узлов имеют вид:
routine OtherNode event; if message = token then out token; ende endrout.
Таким образом "волна", начатая инициатором, заканчивается, когда возвращается к инициатору. Описанный распределенный алгоритм выполняется за время O(n).
Алгоритм можно расширить на случай двунаправленного цикла. Каждый узел имеет двух соседей и связи между ними симметричны (ненаправленны). Поэтому, следует ввести понятия "левого" и "правого" соседа. Инициатор направляет маркер только одному, например, правому соседу, и ожидает возвращения маркера слева. Также поступает и любой другой сайт.
Метод можно использовать и еще для более широкого класса архитектур распределенных систем, в которых существует гамильтонов цикл, проходящий через все сайты. Однако формулировка соответствующего алгоритма будет более сложной: для каждого сайта должен быть определен "сосед справа в гамильтоновом цикле".
Алгоритм для структуры – дерева
Предположим, что соединение сайтов распределенной системы каналами образует граф – неориентированное дерево. Из теории графов известны следующие факты для деревьев:
- дерево – связный ациклический граф;
- количество вершин в дереве на единицу больше, чем количество ребер;
- в нетривиальном дереве имеется, по крайней мере, две вершины, степени которых равны единице; эти вершины называются висячими или терминальными; остальные вершины имеют степень, не меньше 2.
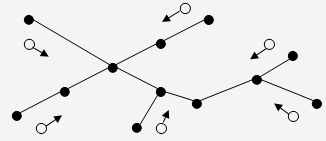
В описываемом алгоритме инициаторами являются все висячие вершины (рис. 12.2). Любой инициатор может передать маркер только одному соседнему сайту. Любой другой сайт v (не инициатор), имеющий степень deg(v), генерирует маркер только в том случае, если получил маркеры от deg(v) – 1 соседа, т.е. от всех смежных сайтов, кроме одного. Тогда сайт v отправляет маркер тому единственному соседу, от которого маркера еще не было (вполне возможно, что этот сосед просто задержался с передачей).
Если задержавшийся сосед все же передаст маркер, т.е. сайт v получит deg(v) маркеров, то сайт v выполнит процедуру return(OK). Выполнение процедуры return(OK) любым из сайтов завершает работу распределенного алгоритма.
Описанный алгоритм не столь очевиден, как алгоритм для кольцевой архитектуры. Поэтому нам нужны гарантии его правильности, а именно, гарантии того, что если какой-либо из сайтов выполнил процедуру return(OK), все остальные сайты vi получили, по крайней мере, по deg(vi) – 1 маркеров и сгенерировали или готовы сгенерировать выходные маркеры.
Рисунки 12.2 – 12.4 иллюстрируют на примере некоторого дерева продвижение маркеров. На шаге 2 вершины, уже получившие маркеры, обозначены соответствующими числами. После выполнения шага 3, вершина, обозначенная " a " и имеющая степень 3, получит последние два маркера. Количество полученных маркеров станет равным трем, и будет выполнена процедура return(OK).
Отметим, что эти рисунки и приведенные выше комментарии к ним справедливы для случая, когда перемещение любого маркера по любому ребру дерева требует одного и того же времени, а генерация маркера происходит мгновенно. Инициаторы также одновременно генерируют свои маркеры.
В противном случае процесс закончится в какой-либо другой (не висячей) вершине дерева. Если же какая-либо из висячих вершин – инициаторов сильно запоздает с генерацией своего маркера, то может возникнуть непредусмотренная ситуация получения маркера висячей вершиной.
Сказанное еще раз подтверждает то, что выполнение распределенного алгоритма не является строго детерминированным во времени, но, тем не менее, при правильном построении алгоритма может быть детерминированным по результатам.