Волновые алгоритмы распространения информации

Фазовый алгоритм

Фазовый алгоритм является децентрализованным алгоритмом для произвольных ориентированных графов. Двунаправленные связи тоже могут присутствовать, но они должны быть заданы парой параллельных встречных однонаправленных каналов (дуг графа). Алгоритм требует, чтобы процессам на сайтах был известен диаметр d графа, либо его оценка сверху.

Переменные в тексте алгоритма имеют следующий смысл.

counter_out – счетчик, подсчитывающий количество маркеров token, посланных каждому из соседей по выходу. Если таких соседей у некоторого сайта, например, три, то за каждой единицей счетчика стоит три посланных маркера – по одному на каждого соседа.

counter_in – массив счетчиков, по одному счетчику на каждого соседа по входу. Хранит количество маркеров, посланных соседями.

this – сайт, процесс которого исполняет данный алгоритм.

Out() – множество вершин, смежных по выходу.

u – некоторый сайт, передавший маркер.

Функция min, примененная к массиву, выбирает из него минимальный элемент.

Алгоритм может использоваться в ориентированных сетях произвольной топологии, где каналы могут передавать сообщения только в одном направлении. В этом случае, соседи s являются соседями по входу (процессы, которые могут посылать сообщения s ) и соседями по выходу (процессы, которым s может посылать сообщения).

В фазовом алгоритме каждый процесс посылает ровно d сообщений каждому соседу по выходу. Только после того, как k сообщений было получено от каждого соседа по входу, (k + 1) -ое сообщение посылается каждому соседу по выходу.

Алгоритм Финна

Алгоритм Финна – еще один волновой алгоритм, который можно использовать в ориентированных сетях произвольной топологии. Он не требует того, чтобы диаметр сети был известен заранее, но подразумевает наличие уникальных идентификаторов процессов. В сообщениях передаются множества идентификаторов процессов, что приводит к довольно высокой битовой сложности алгоритма.

Процесс сайта s содержит два множества идентификаторов процессов, Inc(s) и NInc(s). Неформально говоря, n – это множество процессов u таких, что событие в u предшествует последнему произошедшему событию в s, а NInc(s) – множество процессов u таких, что для всех соседей r процесса u событие в r предшествует последнему произошедшему событию в s. Эта зависимость поддерживается следующим образом.

Изначально Inc(s) = {s}, а 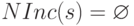. Каждый раз, когда одно из множеств пополняется, процесс s посылает сообщение, включая в него Inc(s) и NInc(s). Когда s получает сообщение, включающее множества Inc(s) и NInc(s), полученные идентификаторы включаются в версии этих множеств в процессе s. Когда s получит сообщения от всех соседей по входу, s включается в NInc(s). Когда два множества становятся равны, s выполняет процедуру return(OK). Из неформального смысла двух множеств следует, что для каждого процесса u такого, что событие в u предшествует некоторому событию e, выполняется следующее: для каждого соседа r процесса u событие в r также предшествует событию e.

При разработке распределенных алгоритмов для различных приложений часто в качестве подзадач возникает несколько общих проблем для сетей процессов. Эти элементарные задачи включают в себя широковещательную рассылку информации – broadcasting (например, посылка начального или заключительного сообщения), достижение глобальной синхронизации между процессами, запуск выполнения некоторого события в каждом процессе, или вычисление функции, входные данные которой распределены между процессами.

Распространение информации с обратной связью

Важным применением волновых алгоритмов является случай, когда некоторая информация должна быть передана всем процессам и определенные процессы должны быть оповещены о завершении передачи. Эта задача распространения информации с обратной связью (PIF – propagation of information with feedback) формулируется следующим образом.

Формируется подмножество процессов из тех, кому известно сообщение M (одно и то же для всех процессов), которое должно быть распространено, т.е. все процессы должны принять M. Определенные процессы должны быть оповещены о завершении передачи; т.е. должно быть выполнено специальное событие notify, причем оно может быть выполнено только когда все процессы уже получили сообщение M. Алгоритм должен использовать конечное количество сообщений.

Оповещение в PIF-алгоритме можно рассматривать как событие return(OK).

Любой волновой алгоритм может использоваться как PIF-алгоритм. Действительно, пусть A – волновой алгоритм. Чтобы использовать A как PIF-алгоритм, возьмем в качестве процессов, изначально знающих M, инициаторы A. Информация M добавляется к каждому сообщению A. Это возможно, поскольку по построению стартеры A знают M изначально, а последователи не посылают сообщений, пока не получат хотя бы одно сообщение, т.е. пока не получат M. Событию return(OK) в волне предшествуют события в каждом процессе; следовательно, когда оно происходит, каждый процесс знает M, и событие return(OK) можно считать требуемым событием notify в PIF-алгоритме.

Синхронизация

Волновые алгоритмы могут использоваться для случаев, когда должна быть достигнута глобальная синхронизация процессов. Задача синхронизации формулируется следующим образом. В каждом процессе q должно быть выполнено событие a_q, и в некоторых процессах должны быть выполнены события b_p, причем все события a_q должны быть выполнены по времени раньше, чем будет выполнено какое-либо событие b_p. Алгоритм должен использовать конечное количество сообщений.

В алгоритмах синхронизации события b_p будут рассматриваться как события return(OK).

Любой волновой алгоритм может использоваться как алгоритм синхронизации. Действительно, пусть A – волновой алгоритм. Чтобы преобразовать A в алгоритм синхронизации, потребуем, чтобы каждый процесс q выполнял a_q до того, как q пошлет сообщение в A или примет решение в A. Событие b_p происходит после события return(OK) в p.

Вычисление нижней грани

Продемонстрируем применение волновых алгоритмов для вычисления функций, значения которых зависят от входов процесса на каждом сайте. В качестве представителей таких функций будут рассмотрены алгоритмы, вычисляющие нижнюю грань по всем входам, которые должны быть извлечены из частично упорядоченного множества.

Как известно из курса математики, если ( X, <= ) – частичный порядок, то c называют нижней гранью a и b, если c <= a, c <= b, и . Допустим, что X таково, что нижняя грань всегда существует; в этом случае нижняя грань является единственной и обозначается как . Так как – бинарный оператор, коммутативный и ассоциативный, то операция может быть обобщена на конечные множества: .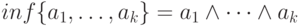

Задача вычисления нижней грани в распределенной системе формулируется следующим образом. Каждый процесс на сайте q содержит вход a_q , являющийся элементом частично упорядоченного множества X. Потребуем, чтобы определенные процессы вычисляли значение inf {a_q} по всем сайтам и чтобы эти процессы знали, когда вычисление завершается. Они записывают результат вычисления в переменную out и после этого не могут изменять ее значение.

Событие write, которое заносит значение в out, рассматривается в алгоритме вычисления нижней грани как событие return(OK).

Любой волновой алгоритм может быть использован для вычисления нижней грани.

Это можно показать следующим образом. Допустим, что дан волновой алгоритм A. Назначим каждому процессу q дополнительную переменную v_q , которой придадим начальное значение a_q . Во время волны эти переменные переприсваиваются следующим образом. Всякий раз, когда процесс q посылает сообщение, текущее значение v_q включается в сообщение. Всякий раз, когда процесс q получает сообщение со значением v, переменной v_q присваивается значение 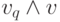. Когда в процессе p происходит событие return(OK), текущее значение v_p заносится в out_p.

Теперь нужно показать, что в результат заносится правильное значение. Обозначим правильный ответ через L, т.е. L = inf {a_q}. Для события a в процессе q обозначим через v^(a) значение v_q сразу после выполнения a. Так как начальное значение v_q равно a_q , и в течение волны оно только уменьшается, неравенство v^(a) <= a_q сохраняется для каждого события a в q. Из присваивания v следует, что для событий a и b, a >= b => v^(a) >= v^(b). Кроме того, так как v всегда вычисляется как нижняя грань двух уже существующих величин, нера венство L <= v выполняется для всех величин в течение волны. Таким образом, если d – событие return(OK) в p, значение v^(d) удовлетворяет неравенству L <= v^(d) и, так как событию d предшествует хотя бы одно событие в каждом процессе q, v^(d) <= a_q для всех q. Отсюда следует, что L = v^(d).

Известна теорема о нижней грани: Если • – бинарный оператор на множестве X, причем он:

1. коммутативен, т.е. a • b = b • a,
2. ассоциативен, т.е. (a • b) • c = a • (b • c),
3. идемпотентен, т.е. a • a = a,

то существует отношение частичного порядка на X такое, что • – функция нижней грани.

Среди операторов, удовлетворяющих этим трем критериям – логическая конъюнкция и дизъюнкция, минимум и максимум целых чисел, наибольший общий делитель и наименьшее общее кратное целых чисел, пересечение и объединение множеств. Отсюда следует, что операции &, 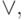min, max, НОД, НОК, и над величинами, локальными по отношению к сайтам, могут быть вычислены за одну волну.