Представление множеств. Деревья. Сбалансированные деревья.
Восстановление сбалансированности требует движения от
листьев к корню, поэтому будем хранить в стеке путь от корня к рассматриваемой в данный момент вершине. Элементами стека будут
пары 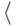 вершина, направление движения из
нее
вершина, направление движения из
нее 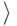 , т.е. значения типа
, т.е. значения типа
record
| vert: 1..n; {вершина}
| direction : (l, r); {l - левое, r - правое}
end;Программа добавления элемента t теперь выглядит так:
if root = null then begin
| get_free (root);
| left[root] := null; right[root] := null; diff[root] := 0;
| val[root] := t;
end else begin
| x := root; ..сделать стек пустым
| {инвариант: осталось добавить t к непустому поддереву с
| корнем в x; стек содержит путь к x}
| while ((t < val [x]) and (left [x] <> null)) or
| | ((t > val [x]) and (right [x] <> null)) do begin
| | if t < val [x] then begin
| | | ..добавить в стек пару <x, l>
| | | x := left [x];
| | end else begin {t > val [x]}
| | | ..добавить в стек пару <x, r>
| | | x := right [x];
| | end;
| end;
| if t <> val [x] then begin {t нет в дереве}
| | get_free (i); val [i] := t;
| | left [i] := null; right [i] := null; diff [i] := 0;
| | if t < val [x] then begin
| | | ..добавить в стек пару <x, l>
| | | left [x] := i;
| | end else begin {t > val [x]}
| | | ..добавить в стек пару <x, r>
| | | right [x] := i;
| | end;
| | d := 1;
| | {инвариант: стек содержит путь к изменившемуся
| | поддереву, высота которого увеличилась по
| | сравнению с высотой в исходном дереве
| | на d (=0 или 1); это поддерево сбалансировано;
| | значения diff для его вершин правильны; в
| | остальном дереве все осталось как было -
| | в частности, значения diff}
| | while (d <> 0) and ..стек непуст do begin {d = 1}
| | | ..взять из стека пару в <v, direct>
| | | if direct = l then begin
| | | | if diff [v] = 1 then begin
| | | | | c := 0;
| | | | end else begin
| | | | | c := 1;
| | | | end;
| | | | diff [v] := diff [v] - 1;
| | | end else begin
| | | {direct = r}
| | | | if diff [v] = -1 then begin
| | | | | c := 0;
| | | | end else begin
| | | | | c := 1;
| | | | end;
| | | | diff [v] := diff [v] + 1;
| | | end;
| | | {c = изменение высоты поддерева с корнем в v по
| | | сравнению с исходным деревом; массив diff
| | | содержит правильные значения для этого поддерева;
| | | возможно нарушение сбалансированности в v}
| | | balance (v, d1); d := c + d1;
| | end;
| end;
end;Легко проверить, что значение d может быть равно только 0 или 1 (но не -1 ): если c=0, то diff[v]=0 и балансировка не производится.
Программа удаления строится аналогично. Ее основной фрагмент таков:
{инвариант: стек содержит путь к изменившемуся поддереву,
высота которого изменилась по сравнению с высотой в
исходном дереве на d (=0 или -1); это поддерево
сбалансировано; значения diff для его вершин правильны;
в остальном дереве все осталось как было -
в частности, значения diff}
while (d <> 0) and ..стек непуст do begin
| {d = -1}
| ..взять из стека пару в <v, direct>
| if direct = l then begin
| | if diff [v] = -1 then begin
| | | c := -1;
| | end else begin
| | | c := 0;
| | end;
| | diff [v] := diff [v] + 1;
| end else begin {direct = r}
| | if diff [v] = 1 then begin
| | | c := -1;
| | end else begin
| | | c := 0;
| | end;
| | diff [v] := diff [v] - 1;
| end;
| {c = изменение высоты поддерева с корнем в v по
| сравнению с исходным деревом; массив diff содержит
| правильные значения для этого поддерева;
| возможно нарушение сбалансированности в v}
| balance (v, d1);
| d := c + d1;
end;Легко проверить, что значение d может быть равно только 0 или -1 (но не -2 ): если c=-1, то diff[v]=0 и балансировка не производится.
Отметим также, что наличие стека делает излишними переменные father и direction (их роль теперь играет вершина стека).
14.2.6. Доказать, что при добавлении элемента
(а) второй из трех случаев балансировки (см.рисунок к задаче 14.2.3.) невозможен;
(б) полная балансировка требует не более одного вращения (после чего все дерево становится сбалансированным), в то время как при удалении элемента может понадобиться много вращений.
Замечание. Мы старались записать программы добавления и удаления так, чтобы они были как можно более похожими друг на друга. Используя специфику каждой из них, можно многое упростить.
Существуют и другие способы представления множеств,
гарантирующие число действий порядка  на каждую
операцию. Опишем один из них (называемый Б-деревьями ).
на каждую
операцию. Опишем один из них (называемый Б-деревьями ).
До сих пор каждая вершина содержала один элемент хранимого
множества. Этот элемент служил границей между левым
и правым поддеревом. Будем теперь хранить в вершине  элементов множества (число
элементов множества (число  может меняться от вершины к вершине, а также при добавлении и удалении новых элементов, см.далее). Эти
может меняться от вершины к вершине, а также при добавлении и удалении новых элементов, см.далее). Эти  элементов служат
разделителями для
элементов служат
разделителями для  поддерева. Пусть фиксировано
некоторое число
поддерева. Пусть фиксировано
некоторое число  . Будем рассматривать деревья,
обладающие такими свойствами:
. Будем рассматривать деревья,
обладающие такими свойствами:
- Каждая вершина содержит от
 до
до 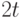 элементов (за исключением корня, который может содержать любое число элементов от
элементов (за исключением корня, который может содержать любое число элементов от  до
до 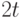 ).
). - Вершина с
 элементами либо имеет
элементами либо имеет  сына, либо не имеет сыновей вообще (является
сына, либо не имеет сыновей вообще (является 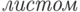 ).
). - Все листья находятся на одной и той же высоте.
Добавление элемента происходит так. Если лист, в который он попадает, неполон (т.е. содержит
менее 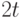 элементов), то нет проблем. Если он полон, то
элементов), то нет проблем. Если он полон, то  элемент (все элементы листа и новый элемент)
разбиваем на два листа по
элемент (все элементы листа и новый элемент)
разбиваем на два листа по  элементов и разделяющий их
серединный элемент. Этот серединный элемент надо добавить
в вершину предыдущего уровня. Это возможно, если в ней
менее
элементов и разделяющий их
серединный элемент. Этот серединный элемент надо добавить
в вершину предыдущего уровня. Это возможно, если в ней
менее 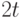 элементов. Если и она полна, то ее разбивают на
две, выделяют серединный элемент и т.д. Если в конце концов
мы захотим добавить элемент в корень, а он окажется полным,
то корень расщепляется на две вершины, а высота дерева
увеличивается на
элементов. Если и она полна, то ее разбивают на
две, выделяют серединный элемент и т.д. Если в конце концов
мы захотим добавить элемент в корень, а он окажется полным,
то корень расщепляется на две вершины, а высота дерева
увеличивается на  .
.
Удаление элемента, находящегося не в листе, сводится к удалению непосредственно следующего за ним,
который находится в листе. Поэтому достаточно научиться удалять
элемент из листа. Если лист при этом становится слишком маленьким,
то его можно пополнить за счет соседнего листа - если только и он не
имеет минимально возможный размер  . Если же оба листа имеют размер
. Если же оба листа имеют размер  , то на них вместе
, то на них вместе 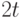 элементов, вместе с разделителем -
элементов, вместе с разделителем -  . После удаления одного элемента остается
. После удаления одного элемента остается 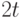 элементов - как раз на один лист. Если при этом вершина предыдущего уровня становится меньше нормы, процесс повторяется и т.д.
элементов - как раз на один лист. Если при этом вершина предыдущего уровня становится меньше нормы, процесс повторяется и т.д.
14.2.7.
Реализовать описанную схему хранения множеств,
убедившись, что она также позволяет обойтись  действий для операций включения, исключения и проверки принадлежности.
действий для операций включения, исключения и проверки принадлежности.
14.2.8.
Можно определять сбалансированность дерева иначе:
требовать, чтобы для каждой вершины ее левое и правое
поддеревья имели не слишком сильно отличающиеся количества
вершин. (Преимущество такого определения состоит в том, что
при вращениях не нарушается сбалансированность в вершинах,
находящихся ниже точки вращения.) Реализовать на основе
этой идеи способ хранения множеств, гарантирующий оценку
в  действий для включения, удаления и проверки
принадлежности.
действий для включения, удаления и проверки
принадлежности.
Указание. Он также использует большие и малые вращения. Подробности см.в книге Рейнгольда, Нивергельта и Део "Комбинаторные алгоритмы".
