Переменные, выражения, присваивания
1.1. Задачи без массивов
1.1.1. Даны две целые переменные a, b. Составить фрагмент программы, после исполнения которого значения переменных поменялись бы местами (новое значение a равно старому значению b и наоборот).
Решение. Введем дополнительную целую переменную t.
t := a; a := b; b := t;
Попытка обойтись без дополнительной переменной, написав
a := b; b := a;
не приводит к цели (безвозвратно утрачивается начальное значение переменной a ).
1.1.2. Решить предыдущую задачу, не используя дополнительных переменных (и предполагая, что значениями целых переменных могут быть произвольные целые числа).
Решение.Начальные значения a и b обозначим a0, b0.
a := a + b; {a = a0 + b0, b = b0}
b := a - b; {a = a0 + b0, b = a0}
a := a - b; {a = b0, b = a0}1.1.3.
Дано целое число а и натуральное (целое
неотрицательное) число n. Вычислить 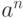 .
Другими словами, необходимо составить программу, при
исполнении которой значения переменных а и n не
меняются, а значение некоторой другой переменной
(например, b ) становится равным
.
Другими словами, необходимо составить программу, при
исполнении которой значения переменных а и n не
меняются, а значение некоторой другой переменной
(например, b ) становится равным 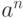 .
(При этом разрешается использовать и другие переменные.)
.
(При этом разрешается использовать и другие переменные.)
Решение. Введем целую переменную k, которая меняется
от 0 до n, причем поддерживается такое свойство: 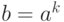 ).
).
k := 0; b := 1;
{b = a в степени k}
while k <> n do begin
| k := k + 1;
| b := b * a;
end;Другое решение той же задачи:
k := n; b := 1;
{a в степени n = b * (a в степени k)}
while k <> 0 do begin
| k := k - 1;
| b := b * a;
end;1.1.4.Решить предыдущую задачу, если требуется, чтобы число
действий (выполняемых операторов присваивания) было порядка  (то есть не превосходило бы
(то есть не превосходило бы  для некоторой константы
для некоторой константы  ;
;  - это степень,
в которую нужно возвести
- это степень,
в которую нужно возвести  , чтобы получить
, чтобы получить  ).
).
Решение. Внесем некоторые изменения во второе из предложенных решений предыдущей задачи:
k := n; b := 1; c:=a;
{a в степени n = b * (c в степени k)}
while k <> 0 do begin
| if k mod 2 = 0 then begin
| | k:= k div 2;
| | c:= c*c;
| end else begin
| | k := k - 1;
| | b := b * c;
| end;
end;Каждый второй раз (не реже) будет выполняться первый вариант оператора выбора (если k нечетно, то после вычитания единицы становится четным), так что за два цикла величина k уменьшается по крайней мере вдвое.
1.1.5.Даны натуральные числа а, b. Вычислить произведение 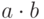 , используя в программе лишь
операции +, -, =, <>.
, используя в программе лишь
операции +, -, =, <>.
Решение.
k := 0; c := 0;
{инвариант: c = a * k}
while k <> b do begin
| k := k + 1;
| c := c + a;
end;
{c = a * k и k = b, следовательно, c = a * b}1.1.6.
Даны натуральные числа а и b. Вычислить их сумму  . Использовать операторы присваивания лишь
вида
. Использовать операторы присваивания лишь
вида
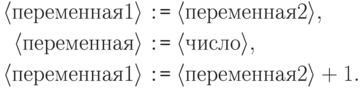
Решение.
...
{инвариант: c = a + k}
...