Переменные, выражения, присваивания
1.1.27.
То же самое, но надо напечатать десятичную запись
в обратном порядке. (Для 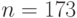 надо напечатать 371.)
надо напечатать 371.)
Решение.
k:= n;
{инвариант: осталось напечатать k в обратном порядке}
while k <> 0 do begin
| write (k mod 10);
| k:= k div 10;
end;1.1.28.
Дано натуральное n. Подсчитать количество решений
неравенства 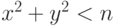 в натуральных
(неотрицательных целых) числах, не используя действий
с вещественными числами.
в натуральных
(неотрицательных целых) числах, не используя действий
с вещественными числами.
Решение.
k := 0; s := 0;
{инвариант: s = количество решений неравенства
x*x + y*y < n c x < k}
while k*k < n do begin
| ...
| {t = число решений неравенства k*k + y*y < n
| с y>=0 (при данном k) }
| k := k + 1;
| s := s + t;
end;
{k*k >= n, поэтому s = количество всех решений
неравенства}Здесь ... - пока еще не написанный кусок программы, который будет таким:
l := 0; t := 0;
{инвариант: t = число решений
неравенства k*k + y*y < n c 0<=y<l }
while k*k + l*l < n do begin
| l := l + 1;
| t := t + 1;
end;
{k*k + l*l >= n, поэтому t = число
всех решений неравенства k*k + y*y < n}1.1.29.
Та же задача, но количество операций должно быть порядка  . (В предыдущем решении, как можно
подсчитать, порядка n операций.)
. (В предыдущем решении, как можно
подсчитать, порядка n операций.)
Решение. Нас интересуют точки решетки (с целыми
координатами) в первом квадранте, попадающие внутрь круга
радиуса  . Интересующее нас множество (назовем
его X ) состоит из объединения вертикальных столбцов
убывающей высоты.
. Интересующее нас множество (назовем
его X ) состоит из объединения вертикальных столбцов
убывающей высоты.
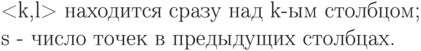
- l - минимальное среди тех
 , для
которых <k,l> не принадлежит X ;
, для
которых <k,l> не принадлежит X ; - s - число пар натуральных
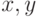 , для
которых
, для
которых 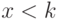 и
и 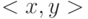 принадлежит X.
принадлежит X.
Обозначим эти условия через (И).
k := 0; l := 0;
while <0,l> принадлежит X do begin
| l := l + 1;
end;
{k = 0, l - минимальное среди тех l >= 0,
для которых <k,l> не принадлежит X}
s := 0;
{инвариант: И}
while not (l = 0) do begin
| s := s + l;
| {s - число точек в столбцах до k-го включительно}
| k := k + 1;
| {точка <k,l> лежит вне X, но, возможно, ее надо сдвинуть
| вниз, чтобы восстановить И}
| while (l <> 0) and (<k, l-1> не принадлежит X) do begin
| | l := l - 1;
| end;
end;
{И, l = 0, поэтому k-ый столбец и все следующие пусты, а
s равно искомому числу}Оценка числа действий очевидна: сначала мы движемся вверх
не более чем на  шагов, а затем вниз
и вправо - в каждую сторону не более чем на
шагов, а затем вниз
и вправо - в каждую сторону не более чем на  шагов.
шагов.
1.1.30.
Даны натуральные числа n и k, 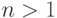 .
Напечатать k десятичных знаков числа
.
Напечатать k десятичных знаков числа 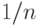 .
(При наличии двух десятичных разложений выбирается то из
них, которое не содержит девятки в периоде.) Программа
должна использовать только целые переменные.
.
(При наличии двух десятичных разложений выбирается то из
них, которое не содержит девятки в периоде.) Программа
должна использовать только целые переменные.
Решение. Сдвинув в десятичной записи числа 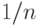 запятую на k мест вправо, получим число
запятую на k мест вправо, получим число 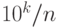 . Нам надо напечатать его целую часть,
то есть разделить
. Нам надо напечатать его целую часть,
то есть разделить 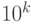 на n нацело.
Стандартный способ требует использования больших по
величине чисел, которые могут выйти за границы диапазона
представимых чисел. Поэтому мы сделаем иначе (следуя
обычному методу "деления уголком") и будем хранить
"остаток" r:
на n нацело.
Стандартный способ требует использования больших по
величине чисел, которые могут выйти за границы диапазона
представимых чисел. Поэтому мы сделаем иначе (следуя
обычному методу "деления уголком") и будем хранить
"остаток" r:
l := 0; r := 1;
{инв.: напечатано l разрядов 1/n, осталось напечатать
k - l разрядов дроби r/n}
while l <> k do begin
| write ( (10 * r) div n);
| r := (10 * r) mod n;
| l := l + 1;
end;1.1.31.
Дано натуральное число  . Определить длину
периода десятичной записи дроби
. Определить длину
периода десятичной записи дроби 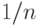 .
.
Решение. Период дроби равен периоду в последовательности
остатков (докажите это; в частности, надо доказать, что он
не может быть меньше). Кроме того, в этой
последовательности все периодически повторяющиеся члены
различны, а предпериод имеет длину не более n. Поэтому
достаточно найти 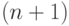 -ый член
последовательности остатков и затем минимальное k, при
котором
-ый член
последовательности остатков и затем минимальное k, при
котором 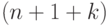 -ый член совпадает
с
-ый член совпадает
с 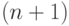 -ым.
-ым.
l := 0; r := 1;
{инвариант: r/n = результат отбрасывания l знаков в 1/n}
while l <> n+1 do begin
| r := (10 * r) mod n;
| l := l + 1;
end;
c := r;
{c = (n+1)-ый член последовательности остатков}
r := (10 * r) mod n;
k := 1;
{r = (n+k+1)-ый член последовательности остатков}
while r <> c do begin
| r := (10 * r) mod n;
| k := k + 1;
end;1.1.32.(Сообщил Ю. В. Матиясевич)
Дана функция 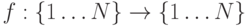 Найти период последовательности
Найти период последовательности 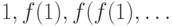 Количество действий
должно быть пропорционально суммарной длине предпериода
и периода (эта сумма может быть существенно меньше N ).
Количество действий
должно быть пропорционально суммарной длине предпериода
и периода (эта сумма может быть существенно меньше N ).
Решение. Если отбросить начальный кусок, последовательность периодична, причем все члены периода различны.
{Обозначение: f[n,1]=f(f(...f(1)...)) (n раз)}
k:=1; a:=f(1); b:=f(f(1));
{a=f[k,1]; b=f[2k,1]}
while a <> b do begin
| k:=k+1; a:=f(a); b:=f(f(b));
end;
{a=f[k,1]=f[2k,1]; f[k,1] входит в периодическую часть}
l:=1; b:=f(a);
{b=f[k+l,1]; f[k,1],...,f[k+l-1,1] различны}
while a <> b do begin
| l:=l+1; b:=f(b);
end;
{период равен l}1.1.33.
(Э. Дейкстра)
Функция f с натуральными аргументами
и значениями определена так:  ,
, 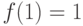 ,
, 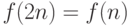 ,
, 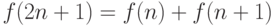 .
Составить программу вычисления
.
Составить программу вычисления 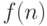 по
заданному n, требующую порядка
по
заданному n, требующую порядка  операций.
операций.
Решение.
k := n; a := 1; b := 0;
{инвариант: 0 <= k, f (n) = a * f(k) + b * f (k+1)}
while k <> 0 do begin
| if k mod 2 = 0 then begin
| | l := k div 2;
| | {k=2l, f(k)=f(l), f(k+1) = f(2l+1) = f(l) + f(l+1),
| | f (n) = a*f(k) + b*f(k+1) = (a+b)*f(l) + b*f(l+1)}
| | a := a + b; k := l;
| end else begin
| | l := k div 2;
| | {k = 2l + 1, f(k) = f(l) + f(l+1),
| | f(k+1) = f(2l+2) = f(l+1),
| | f(n) = a*f(k) + b*f(k+1) = a*f(l) + (a+b)*f(l+1)}
| | b := a + b; k := l;
| end;
end;
{k = 0, f(n) = a * f(0) + b * f(1) = b, что и требовалось}1.1.34.
То же, если 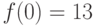 ,
, 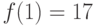 ,
, 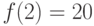 ,
, 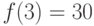 ,
, 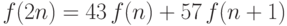 ,
, 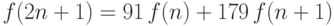 при
при  .
.
Указание.
Хранить коэффициенты в выражении 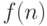 через три
соседних числа.
через три
соседних числа.
1.1.35.
Даны натуральные числа а и b, причем 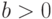 .
Найти частное и остаток при делении a на b,
оперируя лишь с целыми числами и не используя операции div и mod, за исключением деления на 2 четных
чисел; число шагов не должно превосходить
.
Найти частное и остаток при делении a на b,
оперируя лишь с целыми числами и не используя операции div и mod, за исключением деления на 2 четных
чисел; число шагов не должно превосходить 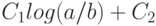 для некоторых констант
для некоторых констант 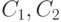
Решение.
b1 := b;
while b1 <= a do begin
| b1 := b1 * 2;
end;
{b1 > a, b1 = b * (некоторая степень 2)}
q:=0; r:=a;
{инвариант: q, r - частное и остаток при делении a на b1,
b1 = b * (некоторая степень 2)}
while b1 <> b do begin
| b1 := b1 div 2 ; q := q * 2;
| { a = b1 * q + r, 0 <= r, r < 2 * b1}
| if r >= b1 then begin
| | r := r - b1;
| | q := q + 1;
| end;
end;
{q, r - частное и остаток при делении a на b}
