Контекстно-свободные грамматики
15.1. Общий алгоритм разбора
Чтобы определить то, что называют контекстно-свободной грамматикой (КС-грамматикой), надо:
- указать конечное множество
 , называемое алфавитом ;
его элементы называют символами ; конечные последовательности
символов называют словами (в данном алфавите);
, называемое алфавитом ;
его элементы называют символами ; конечные последовательности
символов называют словами (в данном алфавите); - разделить все символы алфавита
 на две группы: терминальные ("окончательные") и нетерминальные
("промежуточные");
на две группы: терминальные ("окончательные") и нетерминальные
("промежуточные"); - выбрать среди нетерминальных символов один, называемый начальным ;
- указать конечное число правил грамматики, каждое
из которых должно иметь вид
 ,
где
,
где  - некоторый нетерминальный символ, а
- некоторый нетерминальный символ, а  - слово
(в него могут входить и терминальные, и нетерминальные символы).
- слово
(в него могут входить и терминальные, и нетерминальные символы).
Пусть фиксирована КС-грамматика (мы часто будем опускать
префикс "КС-", так как других грамматик у нас
не будет). Выводом в этой грамматике называется
последовательность слов  , в которой
, в которой 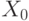 состоит из одного символа, и этот символ - начальный,
а
состоит из одного символа, и этот символ - начальный,
а 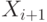 получается из
получается из  заменой некоторого
нетерминального символа
заменой некоторого
нетерминального символа  на слово
на слово  по одному из
правил грамматики. Слово, составленное из терминальных
символов, называется выводимым, если существует
вывод, который им кончается. Множество всех выводимых слов
(из терминальных символов) называется языком,
порождаемым данной грамматикой}.
по одному из
правил грамматики. Слово, составленное из терминальных
символов, называется выводимым, если существует
вывод, который им кончается. Множество всех выводимых слов
(из терминальных символов) называется языком,
порождаемым данной грамматикой}.
В этой и следующей лекции нас будет интересовать такой вопрос: дана КС-грамматика; построить алгоритм, который по любому слову проверяет, выводимо ли оно в этой грамматике.
![\begin{center}\ttfamily
( ) [ ] E
\end{center}](/sites/default/files/tex_cache/5a16569a9ccdc322d3aa286046be0576.png)
![\begin{align*}
\hbox{\texttt{E}} & \to \hbox{\texttt{(E)}}\\
\hbox{\texttt{E}} & \to \hbox{\texttt{[E]}}\\
\hbox{\texttt{E}} & \to \hbox{\texttt{EE}}\\
\hbox{\texttt{E}} & \to
\end{align*}](/sites/default/files/tex_cache/178d42d7f52feb483dca03e71f7ebb48.png)
Примеры выводимых слов:
![\begin{center}\ttfamily
\hspace*{1em} \textrm{(пустое слово)}\\
()\\
([$\,$])\\
()[([$\,$])]\\
\leavevmode \hbox{\texttt{[()[$\,$]()[$\,$]]}}
\end{center}](/sites/default/files/tex_cache/5735c4020da86a921474723e4df75bd3.png)
![\begin{center}\ttfamily
(\\
)(\\
(]\\
([)]
\end{center}](/sites/default/files/tex_cache/3d81f44828e69b1146dc34ebb7acd689.png)
Пример 2. Другая грамматика, порождающая тот же язык:
Правила:
![\begin{align*}
\hbox{\texttt{E}} &\to\\ \hbox{\texttt{E}} &\to\hbox{\texttt{TE}}\\ \hbox{\texttt{T}} &\to\hbox{\texttt{(E)}}\\ \hbox{\texttt{T}} &\to\hbox{\texttt{[E]}}
\end{align*}](/sites/default/files/tex_cache/be97974ce57c545ff894a88eabf8e9bb.png)
Для каждого нетерминального символа можно рассмотреть
множество всех слов из терминальных символов, которые из него
выводятся (аналогично тому, как это сделано для начального
символа в определении выводимости в грамматике). Каждое правило
грамматики можно рассматривать как свойство этих множеств.
Покажем это на примере только что приведенной грамматики. Пусть  и
и  - множества слов (из скобок), выводимых из нетерминалов T и E соответственно. Тогда правилам грамматики соответствуют такие свойства:
- множества слов (из скобок), выводимых из нетерминалов T и E соответственно. Тогда правилам грамматики соответствуют такие свойства:
Сформулированные свойства множеств  ,
,  не определяют эти множества однозначно (например, они остаются верными, если в качестве
не определяют эти множества однозначно (например, они остаются верными, если в качестве  и
и  взять множество всех слов).
Однако можно доказать, что множества, задаваемые
грамматикой, являются минимальными среди удовлетворяющих
этим условиям.
взять множество всех слов).
Однако можно доказать, что множества, задаваемые
грамматикой, являются минимальными среди удовлетворяющих
этим условиям.
15.1.1. Сформулировать точно и доказать это утверждение для произвольной контекстно-свободной грамматики.
15.1.2. Построить грамматику, в которой выводимы слова
(а) 00..0011..11 (число нулей равно числу единиц);
(б) 00..0011..11 (число нулей вдвое больше числа единиц);
(в) 00..0011..11 (число нулей больше числа единиц);
(и только они).
15.1.3. Доказать, что не существует КС-грамматики, в которой были бы выводимы слова вида 00..0011..1122..22, в которых числа нулей, единиц и двоек равны, и только они.
Указание.
Доказать следующую лемму о произвольной
КС-грамматике: для любого достаточно длинного слова  , выводимого в этой грамматике, существует такое его представление в виде
, выводимого в этой грамматике, существует такое его представление в виде  , что любое слово вида
, что любое слово вида 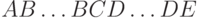 ,
где
,
где  и
и  повторены одинаковое число раз, также выводимо в этой
грамматике. (Это можно установить, найдя нетерминальный символ,
оказывающийся своим собственным "наследником" в процессе вывода.)
повторены одинаковое число раз, также выводимо в этой
грамматике. (Это можно установить, найдя нетерминальный символ,
оказывающийся своим собственным "наследником" в процессе вывода.)
Нетерминальный символ можно рассматривать как "родовое имя" для выводимых из него слов. В следующем примере для наглядности в качестве нетерминальных символов использованы фрагменты русских слов, заключенные в угловые скобки. (С точки зрения грамматики каждый такой фрагмент - один символ!)
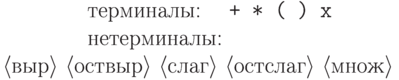
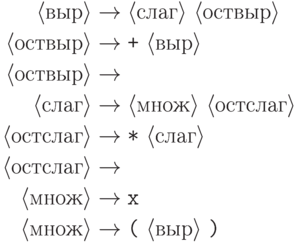
 - это
последовательность слагаемых
- это
последовательность слагаемых  , разделенных плюсами, слагаемое - это последовательность множителей
, разделенных плюсами, слагаемое - это последовательность множителей  ,
разделенных звездочками (знаками умножения), а множитель - это
либо буква x, либо выражение в скобках.
,
разделенных звездочками (знаками умножения), а множитель - это
либо буква x, либо выражение в скобках.
