Порождение комбинаторных объектов
Здесь собраны задачи, в которых требуется получить один за другим все элементы некоторого множества.
2.1. Размещения с повторениями
2.1.1. Напечатать все последовательности длины k из чисел 1..n.
Решение. Будем печатать их в лексикографическом порядке (последовательность a предшествует последовательности b, если для некоторого s их начальные отрезки длины s равны, а (s+1) -ый член последовательности a меньше). Первой будет последовательность <1,1,...,1>, последней - последовательность <n,n,...,n>. Будем хранить последнюю напечатанную последовательность в массиве x[1]..x[k].
...x[1]...x[k] положить равными 1
...напечатать x
...last[1]...last[k] положить равным n
{напечатаны все до x включительно}
while x <> last do begin
| ...x := следующая за x последовательность
| ...напечатать x
end;Опишем, как можно перейти от x к следующей последовательности. Согласно определению, у следующей последовательности первые s членов должны быть такими же, а (s+1) -ый - больше. Это возможно, если x[s+1] меньше n. Среди таких s нужно выбрать наибольшее (иначе полученная последовательность не будет непосредственно следующей). Соответствующее x[s+1] нужно увеличить на 1. Итак, надо, двигаясь с конца последовательности, найти самый правый член, меньший n (он найдется, т.к по предположению x<>last ), увеличить его на 1, а идущие за ним члены положить равными 1.
p:=k;
while not (x[p] < n) do begin
| p := p-1;
end;
{x[p] < n, x[p+1] =...= x[k] = n}
x[p] := x[p] + 1;
for i := p+1 to k do begin
| x[i]:=1;
end;Замечание. Если членами последовательности считать числа не от 1 до n, а от 0 до n-1, то переход к следующему соответствует прибавлению единицы в n -ичной системе счисления.
2.1.2. В предложенном алгоритме используется сравнение двух массивов ( x <> last ). Устранить его, добавив булевскую переменную l и включив в инвариант соотношение
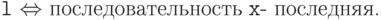
2.1.3. Напечатать все подмножества множества {1...k}.
Решение. Подмножества находятся во взаимно однозначном соответствии с последовательностями нулей и единиц длины k.
2.1.4. Напечатать все последовательности положительных целых чисел длины k, у которых i -ый член не превосходит i.
2.2. Перестановки
2.2.1. Напечатать все перестановки чисел 1..n (то есть последовательности длины n, в которые каждое из этих чисел входит по одному разу).
Решение. Перестановки будем хранить в массиве x[1]..x[n] и печатать в лексикографическом порядке.
(Первой при этом будет перестановка  , последней -
, последней - 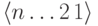 . Для составления
алгоритма перехода к следующей перестановке зададимся
вопросом: в каком случае k -ый член перестановки
можно увеличить, не меняя предыдущих? Ответ: если он меньше
какого-либо из следующих членов (т.е. членов с номерами
больше k ). Мы должны найти наибольшее k, при
котором это так, т.е. такое k, что
. Для составления
алгоритма перехода к следующей перестановке зададимся
вопросом: в каком случае k -ый член перестановки
можно увеличить, не меняя предыдущих? Ответ: если он меньше
какого-либо из следующих членов (т.е. членов с номерами
больше k ). Мы должны найти наибольшее k, при
котором это так, т.е. такое k, что
![{x[k]} < {x[k+1]} > \ldots > {x[n]}](/sites/default/files/tex_cache/0bcd51a4fe18ec8afabe912250ab6080.png)
Алгоритм перехода к следующей перестановке:
{<x[1]...x[n]> <> <n...2,1>}
k:=n-1;
{последовательность справа от k убывающая: x[k+1]>...>x[n]}
while x[k] > x[k+1] do begin
| k:=k-1;
end;
{x[k] < x[k+1] > ... > x[n]}
t:=k+1;
{t <=n, все члены отрезка x[k+1] > ... > x[t] больше x[k]}
while (t < n) and (x[t+1] > x[k]) do begin
| t:=t+1;
end;
{x[k+1] > ... > x[t] > x[k] > x[t+1] > ... > x[n]}
... обменять x[k] и x[t]
{x[k+1] > ... > x[n]}
... переставить участок x[k+1] ... x[n] в обратном порядкеЗамечание. Программа имеет знакомый дефект: если t=n, то x[t+1] не определено.
