Сортировка
4.1. Квадратичные алгоритмы
4.1.1.
Пусть ![{a[1]},\ldots,{a[n]}](/sites/default/files/tex_cache/78e872883833cd02b1d589edbcfe3f5e.png) - целые числа. Требуется
построить массив
- целые числа. Требуется
построить массив ![{b[1]},\ldots,{b[n]}](/sites/default/files/tex_cache/cbc9e080fe566e8cce023eaa6fabe52a.png) , содержащий те
же числа, для которого
, содержащий те
же числа, для которого ![{b[1]}\le\ldots\le{b[n]}](/sites/default/files/tex_cache/318c387b3bd65255d14a8d1219425065.png) .
.
Замечание. Среди чисел ![{a[1]}\ldots{a[n]}](/sites/default/files/tex_cache/dce62e79eefc8a3d30d7b9890da6b90f.png) могут быть
равные. Требуется, чтобы каждое целое число входило
в
могут быть
равные. Требуется, чтобы каждое целое число входило
в ![{b[1]}\ldots{b[n]}](/sites/default/files/tex_cache/d90e4f87f7ef75bbded4fc18991103da.png) столько же раз, сколько и в
столько же раз, сколько и в ![{a[1]}\ldots{a[n]}](/sites/default/files/tex_cache/dce62e79eefc8a3d30d7b9890da6b90f.png) .
.
Решение.
Удобно считать, что числа ![{a[1]}\ldots{a[n]}](/sites/default/files/tex_cache/dce62e79eefc8a3d30d7b9890da6b90f.png) и
и ![{b[1]}\ldots{b[n]}](/sites/default/files/tex_cache/d90e4f87f7ef75bbded4fc18991103da.png) представляют собой начальное
и конечное значения массива x. Требование " a
и b содержат одни и те же числа" будет заведомо
выполнено, если в процессе работы мы ограничимся
перестановками элементов x.
представляют собой начальное
и конечное значения массива x. Требование " a
и b содержат одни и те же числа" будет заведомо
выполнено, если в процессе работы мы ограничимся
перестановками элементов x.
k := 0;
{k наименьших элементов массива установлены на свои места}
while k <> n do begin
| s := k + 1; t := k + 1;
| {x[s] - наименьший среди x[k+1]...x[t] }
| while t<>n do begin
| | t := t + 1;
| | if x[t] < x[s] then begin
| | | s := t;
| | end;
| end;
| {x[s] - наименьший среди x[k+1]..x[n] }
| ... переставить x[s] и x[k+1];
| k := k + 1;
end;4.1.2.
Дать другое решение задачи сортировки, использующее
инвариант "первые k элементов упорядочены"
( ![{x[1]}\le\ldots\le{x[k]}](/sites/default/files/tex_cache/a01dca04be06cf797d0b5e6b0cd66209.png) ).
).
Решение.
k:=1;
{первые k элементов упорядочены}
while k <> n do begin
| t := k+1;
| {k+1-ый элемент продвигается к началу, пока не займет
| надлежащего места, t - его текущий номер}
| while (t > 1) and (x[t] < x[t-1]) do begin
| | ...поменять x[t-1] и x[t];
| | t := t - 1;
| end;
end;Замечание. Дефект программы: при ложном выражении (t>1)
проверка ![{x[t]}<{x[t-1]}](/sites/default/files/tex_cache/68ffe657b9bf7c48b535b08a8dc87afb.png) требует несуществующего
значения x[0].
требует несуществующего
значения x[0].
Оба предложенных решения требуют числа действий,
пропорционального 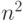 . Существуют более эффективные
алгоритмы.
. Существуют более эффективные
алгоритмы.
4.2. Алгоритмы порядка n log n
4.2.1.
Предложить алгоритм сортировки за время  (число
операций при сортировке
(число
операций при сортировке  элементов не больше
элементов не больше 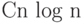 для некоторого
для некоторого  и для
всех
и для
всех  ).
).
Мы предложим два решения.
Решение 1 (сортировка слиянием).
Пусть k - положительное целое число. Разобьем массив ![{x[1]}\ldots{x[n]}](/sites/default/files/tex_cache/716647067f5d76102fd209a2c165c0db.png) на отрезки
длины k. (Первый -
на отрезки
длины k. (Первый - ![{x[1]}\ldots{x[k]}](/sites/default/files/tex_cache/ed7ba99c83b01980f423a7ad385d6639.png) , затем
, затем ![{x[k+1]}\ldots{x[2k]}](/sites/default/files/tex_cache/98456b0edf6068bc15e56c26848ca7df.png) и так
далее.) Последний отрезок будет неполным, если n не
делится на k. Назовем массив k-упорядоченным,
если каждый из этих отрезков в отдельности упорядочен.
Любой массив 1-упорядочен. Если массив k-упорядочен и
и так
далее.) Последний отрезок будет неполным, если n не
делится на k. Назовем массив k-упорядоченным,
если каждый из этих отрезков в отдельности упорядочен.
Любой массив 1-упорядочен. Если массив k-упорядочен и  , то он упорядочен.
, то он упорядочен.
Мы опишем, как преобразовать k-упорядоченный массив в 2k-упорядоченный (из тех же элементов). С помощью этого преобразования алгоритм записывается так:
k:=1;
{массив x является k-упорядоченным}
while k < n do begin
| ...преобразовать k-упорядоченный массив в 2k-упорядоченный;
| k := 2 * k;
end;Требуемое преобразование состоит в том,что мы многократно "сливаем" два упорядоченных отрезка длины не больше k в один упорядоченный отрезок. Пусть процедура

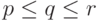 сливает отрезки
сливает отрезки ![{x[p+1]}\ldots{x[q]}](/sites/default/files/tex_cache/903bb8e0517be3a71c9e2cee76d9539c.png) и
и ![{x[q+1]}\ldots{x[r]}](/sites/default/files/tex_cache/6eb30670716c47d106f87c4667f8132b.png) в упорядоченный отрезок
в упорядоченный отрезок ![{x[p+1]}\ldots{x[r]}](/sites/default/files/tex_cache/490ff857fecb6b66c1b595f6823d7fd7.png) (не
затрагивая других частей массива x ).
(не
затрагивая других частей массива x ).Тогда преобразование k -упорядоченного массива в 2k -упорядоченный осуществляется так:
t:=0;
{t кратно 2k или t = n, x[1]..x[t] является
2k-упорядоченным; остаток массива x не изменился}
while t + k < n do begin
| p := t;
| q := t+k;
| r := min (t+2*k, n);
| {min(a,b) - минимум из a и b}
| слияние (p,q,r);
| t := r;
end;Слияние требует вспомогательного массива для записи результатов слияния - обозначим его b. Через p0 и q0 обозначим номера последних элементов участков, подвергшихся слиянию, s0 - последний записанный в массив b элемент. На каждом шаге слияния производится одно из двух действий:
b[s0+1]:=x[p0+1]; p0:=p0+1; s0:=s0+1;
или
b[s0+1]:=x[q0+1]; q0:=q0+1; s0:=s0+1;
(Любители языка C написали бы в этом случае b[++s0]=x[++p0] и b[++s0]=x[++q0].)

