Сортировка
4.3. Применения сортировки.
4.3.1.
Найти количество различных чисел среди элементов данного
массива. Число действий порядка  . (Эта задача
уже была в
"Переменные, выражения, присваивания"
.)
. (Эта задача
уже была в
"Переменные, выражения, присваивания"
.)
Решение. Отсортировать числа, а затем посчитать количество различных, просматривая элементы массива по порядку.
4.3.2.
Дано n отрезков ![[{a[i]},{b[i]}]](/sites/default/files/tex_cache/d6b8d5fdd58224ac25a3e511c7aed475.png) на прямой
(
на прямой
(  ). Найти максимальное k, для
которого существует точка прямой, покрытая k отрезками
("максимальное число слоев"). Число действий - порядка
). Найти максимальное k, для
которого существует точка прямой, покрытая k отрезками
("максимальное число слоев"). Число действий - порядка 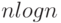 .
.
Решение. Упорядочим все левые и правые концы отрезков вместе (при этом левый конец считается меньше правого конца, расположенного в той же точке прямой). Далее двигаемся слева направо, считая число слоев. Встреченный левый конец увеличивает число слоев на 1, правый - уменьшает. Отметим, что примыкающие друг к другу отрезки обрабатываются правильно: сначала идет левый конец (правого отрезка), а затем - правый (левого отрезка).
4.3.3.
Дано  точек на плоскости. Указать
точек на плоскости. Указать 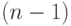 -звенную
несамопересекающуюся незамкнутую ломаную, проходящую через
все эти точки. (Соседним отрезкам ломаной разрешается
лежать на одной прямой.) Число действий порядка
-звенную
несамопересекающуюся незамкнутую ломаную, проходящую через
все эти точки. (Соседним отрезкам ломаной разрешается
лежать на одной прямой.) Число действий порядка  .
.
Решение. Упорядочим точки по  -координате, а при
равных
-координате, а при
равных  -координатах - по
-координатах - по  -координате. В таком
порядке и можно проводить ломаную.
-координате. В таком
порядке и можно проводить ломаную.
4.3.4. Та же задача, если ломаная должна быть замкнутой.
Решение. Возьмем самую левую точку (то есть точку
с наименьшей  -координатой) и проведем из нее лучи во
все остальные точки. Теперь упорядочим эти лучи снизу
вверх, а точки на одном луче упорядочим по расстоянию от
начала луча (это делается для всех лучей, кроме нижнего
и верхнего). Ломаная выходит из выбранной (самой левой)
точки по нижнему лучу, затем по всем остальным лучам
(в описанном порядке) и возвращается по верхнему лучу.
-координатой) и проведем из нее лучи во
все остальные точки. Теперь упорядочим эти лучи снизу
вверх, а точки на одном луче упорядочим по расстоянию от
начала луча (это делается для всех лучей, кроме нижнего
и верхнего). Ломаная выходит из выбранной (самой левой)
точки по нижнему лучу, затем по всем остальным лучам
(в описанном порядке) и возвращается по верхнему лучу.
4.3.5.
Дано  точек на плоскости. Построить их выпуклую
оболочку - минимальную выпуклую фигуру, их содержащую.
(Резиновое колечко, натянутое на вбитые в доску гвозди - их
выпуклая оболочка.) Число операций не более
точек на плоскости. Построить их выпуклую
оболочку - минимальную выпуклую фигуру, их содержащую.
(Резиновое колечко, натянутое на вбитые в доску гвозди - их
выпуклая оболочка.) Число операций не более  .
.
Указание. Упорядочим точки - годится любой из порядков, использованных в двух предыдущих задачах. Затем, рассматривая точки по очереди, будем строить выпуклую оболочку уже рассмотренных точек. (Для хранения выпуклой оболочки полезно использовать дек, см. "Типы данных" . Впрочем, при упорядочении точек по углам это излишне.)
4.4. Нижние оценки для числа сравнений при сортировке
Пусть имеется  различных по весу камней и весы, которые
позволяют за одно взвешивание определить, какой из двух
выбранных нами камней тяжелее. (В программистских терминах:
мы имеем доступ к функции тяжелее(i,j:1..n):boolean.)
Надо упорядочить камни по весу, сделав как можно меньше
взвешиваний (вызовов функции тяжелее ).
различных по весу камней и весы, которые
позволяют за одно взвешивание определить, какой из двух
выбранных нами камней тяжелее. (В программистских терминах:
мы имеем доступ к функции тяжелее(i,j:1..n):boolean.)
Надо упорядочить камни по весу, сделав как можно меньше
взвешиваний (вызовов функции тяжелее ).
Разумеется, число взвешиваний зависит не только от выбранного нами алгоритма, но и от того, как оказались расположены камни. Сложностью алгоритма назовем число взвешиваний при наихудшем расположении камней.
4.4.1.
Доказать, что сложность произвольного алгоритма сортировки  камней не меньше
камней не меньше 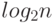 ! (где
! (где 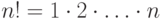 ).
).
Решение. Пусть имеется алгоритм сложности не более  .
Для каждого из
.
Для каждого из  ! возможных расположений камней
запротоколируем результаты взвешиваний (обращений к функции тяжелее ); их можно записать в виде последовательности
из не более чем
! возможных расположений камней
запротоколируем результаты взвешиваний (обращений к функции тяжелее ); их можно записать в виде последовательности
из не более чем  нулей и единиц. Для единообразия
дополним последовательность нулями, чтобы ее длина стала
равной
нулей и единиц. Для единообразия
дополним последовательность нулями, чтобы ее длина стала
равной  . Тем самым у нас имеется
. Тем самым у нас имеется  !
последовательностей из
!
последовательностей из  нулей и единиц. Все эти
последовательности разные - иначе наш алгоритм дал бы
одинаковые ответы для разных порядков (и один из ответов
был бы неправильным). Получаем, что
нулей и единиц. Все эти
последовательности разные - иначе наш алгоритм дал бы
одинаковые ответы для разных порядков (и один из ответов
был бы неправильным). Получаем, что 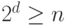 ! - что
и требовалось доказать.
! - что
и требовалось доказать.
Другой способ объяснить то же самое - рассмотреть дерево
вариантов, возникающее в ходе выполнения алгоритма,
и сослаться на то, что дерево высоты  не может иметь
более
не может иметь
более 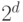 листьев.
листьев.
Несложно заметить, что 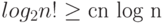 при
подходящем
при
подходящем  , поскольку в сумме
, поскольку в сумме
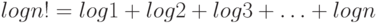
 каждое.
каждое.Тем самым любой алгоритм сортировки, использующий только
сравнения элементов массива и их перестановки, требует не
менее 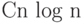 действий, так что наши алгоритмы близки
к оптимальным. Однако алгоритм сортировки, использующий
другие операции, может действовать и быстрее. Вот один из
примеров.
действий, так что наши алгоритмы близки
к оптимальным. Однако алгоритм сортировки, использующий
другие операции, может действовать и быстрее. Вот один из
примеров.
4.4.2.
Имеется массив целых чисел ![{a[1]}\ldots{a[n]}](/sites/default/files/tex_cache/dce62e79eefc8a3d30d7b9890da6b90f.png) , причем
все числа неотрицательны и не превосходят m.
Отсортировать этот массив; число действий порядка
, причем
все числа неотрицательны и не превосходят m.
Отсортировать этот массив; число действий порядка  .
.
Решение. Для каждого числа от 0 до m подсчитываем, сколько раз оно встречается в массиве. После этого исходный массив можно стереть и заполнить заново в порядке возрастания, используя сведения о кратности каждого числа.
Отметим, что этот алгоритм не переставляет числа в массиве, как большинство других, а "записывает их туда заново".
Есть также метод сортировки, в котором последовательно проводится ряд "частичных сортировок" по отдельным битам. Начнем с такой задачи.
4.4.3.
В массиве ![{a[1]}\ldots{a[n]}](/sites/default/files/tex_cache/dce62e79eefc8a3d30d7b9890da6b90f.png) целых чисел переставить
элементы так, чтобы четные числа шли перед нечетными (не
меняя взаимный порядок в каждой из групп).
целых чисел переставить
элементы так, чтобы четные числа шли перед нечетными (не
меняя взаимный порядок в каждой из групп).
Решение. Сначала спишем (во вспомогательный массив) все четные, а потом - все нечетные.
4.4.4.
Имеется массив из  чисел от
чисел от  до
до  , каждое из
которых мы будем рассматривать как
, каждое из
которых мы будем рассматривать как  -битовое слово из
нулей и единиц. Используя проверки "
-битовое слово из
нулей и единиц. Используя проверки "  -ый бит
равен
-ый бит
равен  " и "
" и "  -ый бит
равен
-ый бит
равен  " вместо
сравнений, отсортировать все числа за время
порядка
" вместо
сравнений, отсортировать все числа за время
порядка 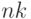 .
.
Решение. Отсортируем числа по последнему биту
(см. предыдущую задачу), затем по предпоследнему и так
далее. В результате они будут отсортированы. В самом деле,
индукцией по  легко доказать, что после
легко доказать, что после  шагов
любые
два числа, отличающиеся только в
шагов
любые
два числа, отличающиеся только в  последних битах, идут
в правильном порядке. (Вариант: после
последних битах, идут
в правильном порядке. (Вариант: после  шагов
шагов  -битовые концы чисел идут в правильном порядке.)
-битовые концы чисел идут в правильном порядке.)
Аналогичный алгоритм может быть применен для  -ичной
системы счисления вместо двоичной. При этом полезна такая
вспомогательная задача:
-ичной
системы счисления вместо двоичной. При этом полезна такая
вспомогательная задача:
4.4.5.
Даны  чисел и функция
чисел и функция  , принимающая (на них)
значения
, принимающая (на них)
значения  . Требуется переставить числа в таком
порядке, чтобы значения функции
. Требуется переставить числа в таком
порядке, чтобы значения функции  не убывали (сохраняя
порядок для чисел с равными значениями
не убывали (сохраняя
порядок для чисел с равными значениями  ). Число действий
порядка
). Число действий
порядка  .
.
Указание.
Завести  списков суммарной длины
списков суммарной длины  (как это сделать,
смотри в
"Типы данных"
о типах данных)
и помещать
в
(как это сделать,
смотри в
"Типы данных"
о типах данных)
и помещать
в  -ый список числа, для которых значение
функции
-ый список числа, для которых значение
функции  равно
равно  . Вариант: посчитать для всех
. Вариант: посчитать для всех  , сколько
имеется
чисел
, сколько
имеется
чисел  с
с 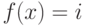 , после чего легко определить,
с какого
места нужно начинать размещать числа
, после чего легко определить,
с какого
места нужно начинать размещать числа  с
с 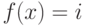 .
.
4.4.6.
Даны  целых чисел в диапазоне от
целых чисел в диапазоне от  до
до 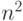 . Как
отсортировать их, сделав порядка
. Как
отсортировать их, сделав порядка  действий?
действий?
