Представление множеств. Деревья. Сбалансированные деревья.
14.2. Сбалансированные деревья
Дерево называется сбалансированным
(или АВЛ-деревом в честь изобретателей этого метода
Г.М. Адельсона-Вельского и E.М. Ландиса), если для
любой его вершины высоты левого и правого поддеревьев этой
вершины отличаются не более чем на  . (В частности, когда
одного из сыновей нет, другой - если он есть - обязан быть
листом.)
. (В частности, когда
одного из сыновей нет, другой - если он есть - обязан быть
листом.)
14.2.1.
Найти минимальное и максимальное возможное
количество вершин в сбалансированном дереве высоты  .
.
Решение. Максимальное число вершин равно  .
Если
.
Если 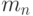 - минимальное число вершин, то, как легко
видеть,
- минимальное число вершин, то, как легко
видеть, 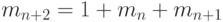 , откуда
, откуда 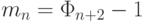 (
(  -
-  -ое число
Фибоначчи,
-ое число
Фибоначчи,  ,
, 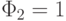 ,
, 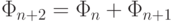 ).
).
14.2.2.
Доказать, что сбалансированное дерево с  вершинами
имеет высоту не больше
вершинами
имеет высоту не больше  для некоторой
константы
для некоторой
константы  , не
зависящей от
, не
зависящей от  .
.
Решение. Индукцией по  легко доказать, что
легко доказать, что 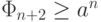 , где
, где  - больший корень квадратного уравнения
- больший корень квадратного уравнения 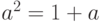 , то есть
, то есть 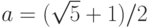 . Остается воспользоваться предыдущей задачей.
. Остается воспользоваться предыдущей задачей.
Вращения
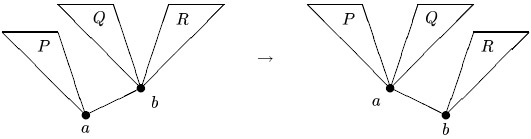
Мы хотим восстанавливать сбалансированность дерева после включения и удаления элементов. Для этого необходимы какие-то преобразования дерева, не меняющие множества пометок на его вершинах и не нарушающие упорядоченности, но способствующие лучшей сбалансированности. Опишем несколько таких преобразований.
Пусть вершина  имеет правого сына
имеет правого сына  . Обозначим
через
. Обозначим
через  левое поддерево вершины
левое поддерево вершины  ,
через
,
через  и
и  -
левое и правое поддеревья вершины
-
левое и правое поддеревья вершины  . Упорядоченность дерева требует, чтобы
. Упорядоченность дерева требует, чтобы 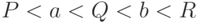 (точнее
следовало бы сказать "любая пометка на
(точнее
следовало бы сказать "любая пометка на  меньше
пометки на
меньше
пометки на  ", "пометка на
", "пометка на  меньше любой
пометки
на
меньше любой
пометки
на  " и т.д., но мы позволим себе этого не делать). Точно
того же требует упорядоченность дерева с корнем
" и т.д., но мы позволим себе этого не делать). Точно
того же требует упорядоченность дерева с корнем  , его
левым сыном
, его
левым сыном  , в котором
, в котором  и
и  - левое
и правое
поддеревья
- левое
и правое
поддеревья  ,
,  - правое поддерево
- правое поддерево  .
Поэтому первое
дерево можно преобразовать во второе, не нарушая
упорядоченности. Такое преобразование назовем малым
правым вращением (правым - поскольку существует симметричное, левое,
малым - поскольку есть и большое, которое мы сейчас опишем).
.
Поэтому первое
дерево можно преобразовать во второе, не нарушая
упорядоченности. Такое преобразование назовем малым
правым вращением (правым - поскольку существует симметричное, левое,
малым - поскольку есть и большое, которое мы сейчас опишем).
Пусть  - правый сын
- правый сын  ,
,  - левый
сын
- левый
сын  ,
,  -
левое поддерево
-
левое поддерево  ,
,  и
и  - левое
и правое
поддеревья
- левое
и правое
поддеревья  ,
,  - правое поддерево
- правое поддерево  .
Тогда
.
Тогда 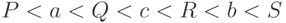 .
.
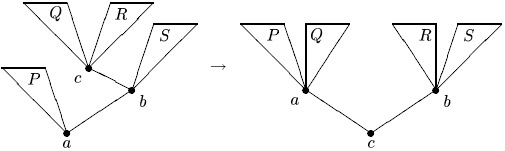
Такой же порядок соответствует дереву с корнем  , имеющим
левого сына
, имеющим
левого сына  и правого сына
и правого сына  , для которого
, для которого  и
и  - поддеревья вершины
- поддеревья вершины  ,
а
,
а  и
и  -
поддеревья вершины
-
поддеревья вершины  . Соответствующее преобразование
будем называть большим правым вращением. (Аналогично
определяется симметричное ему большое левое
вращение.)
. Соответствующее преобразование
будем называть большим правым вращением. (Аналогично
определяется симметричное ему большое левое
вращение.)
14.2.3.
Дано дерево, сбалансированное всюду, кроме корня, в котором
разница высот равна  (т.е. левое и правое поддеревья
корня сбалансированы и их высоты отличаются на
(т.е. левое и правое поддеревья
корня сбалансированы и их высоты отличаются на  ).
Доказать, что оно может быть превращено в сбалансированное
одним из четырех описанных преобразований, причем высота
его останется прежней или уменьшится на
).
Доказать, что оно может быть превращено в сбалансированное
одним из четырех описанных преобразований, причем высота
его останется прежней или уменьшится на  .
.
Решение. Пусть более низким является, например, левое
поддерево, и его высота равна  . Тогда высота правого поддерева равна
. Тогда высота правого поддерева равна  . Обозначим корень через
. Обозначим корень через  , а его правого сына (он
обязательно есть) через
, а его правого сына (он
обязательно есть) через  . Рассмотрим левое и правое поддеревья вершины
. Рассмотрим левое и правое поддеревья вершины  . Одно из них обязательно имеет высоту
. Одно из них обязательно имеет высоту  , а другое
может иметь высоту
, а другое
может иметь высоту  или
или  (меньше
(меньше  быть не может, так как
поддеревья сбалансированы). Если высота левого поддерева равна
быть не может, так как
поддеревья сбалансированы). Если высота левого поддерева равна  , а правого -
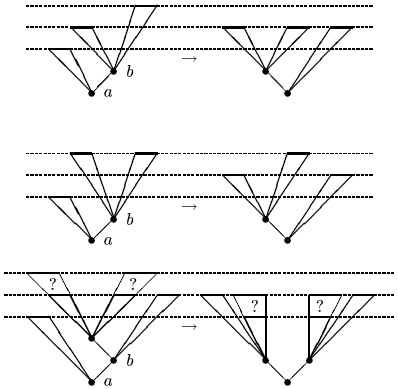
, а правого -  , то потребуется большое правое вращение; в остальных случаях помогает малое. Вот как выглядят три случая балансировки дерева:
, то потребуется большое правое вращение; в остальных случаях помогает малое. Вот как выглядят три случая балансировки дерева: