Представление множеств. Деревья. Сбалансированные деревья.

Хранение деревьев в программе

Можно было бы сопоставить вершины полного двоичного дерева С числами 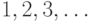(считая, что левый сын есть , правый сын есть 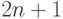) и хранить пометки в массиве val [1...]. Однако этот способ неэкономен, поскольку тратится место на хранение пустых вакансий в полном двоичном дереве.

Более экономен такой способ. Введем три массива

val: array [1..n] of T;
left, right: array [1..n] of 0..n;

( n - максимальное возможное число вершин дерева) И переменную root:0..n. Каждая вершина хранимого -дерева будет иметь номер - число от 1 до n. Разные вершины будут иметь разные номера. Пометка в вершине с номером x равна val[x]. Корень имеет номер root. Если вершина с номером i имеет сыновей, то их номера равны left[i] и right[i]. Отсутствующим сыновьям соответствует число 0. Аналогичным образом значение root=0 соответствует пустому дереву.

Для хранения дерева используется лишь часть массива; для тех i, которые свободны (не являются номерами вершин), значения val[i] безразличны. Нам будет удобно, чтобы все свободные числа были "связаны в список": первое хранится в специальной переменной free:0..n, а следующее за i свободное число хранится в left[i], так что свободны числа

Замечание.Мы использовали для связывания свободных вершин массив left, но, конечно, с тем же успехом можно было использовать массив right.

Вместо значения 0 (обозначающего отсутствие вершины) можно было бы воспользоваться любым другим числом вне 1..n. Чтобы подчеркнуть это, будем вместо 0 использовать константу null=0.

14.1.2. Составить программу, определяющую, содержится ли элемент t:T в упорядоченном дереве (хранимом так, как только что описано).

Решение.

if root = null then begin
| ..не принадлежит
end else begin
| x := root;
| {инвариант: остается проверить наличие t в непустом
|   поддереве с корнем x}
| while ((t < val [x]) and (left [x] <> null)) or
| |     ((t > val [x]) and (right [x] <> null)) do begin
| | if t < val [x] then begin {left [x] <> null}
| | | x := left [x];
| | end else begin {t > val [x], right [x] <> null}
| | | x := right [x];
| | end;
| end;
| {либо t = val [x], либо t отсутствует в дереве}
| ..ответ = (t = val [x])
end;

14.1.3. Упростить решение, используя следующий трюк. Расширим область определения массива val, добавив ячейку с номером null и положим val[null]=t.

Решение.

val [null] := t;
x := root;
while t <> val [x] do begin
| if t < val [x] then begin
| | x := left [x];
| end else begin
| | x := right [x];
| end;
end;
..ответ: (x <> null).

14.1.4. Составить программу добавления элемента t в множество, представленное упорядоченным деревом (если элемент t уже есть, ничего делать не надо).

Решение. Определим процедуру get_free (var i:integer), дающую свободное (не являющееся номером) число i и соответствующим образом корректирующую список свободных чисел.

procedure get_free (var i: integer);
begin
| {free <> null}
| i := free;
| free := left [free];
end;

С ее использованием программа приобретает такой вид:

if root = null then begin
| get_free (root);
| left [root] := null; right [root] := null;
| val [root] := t;
end else begin
| x := root;
| {инвариант: осталось добавить t к непустому поддереву с
|  корнем в x}
| while ((t < val [x]) and (left [x] <> null)) or
| |     ((t > val [x]) and (right [x] <> null)) do begin
| | if t < val [x] then begin
| | | x := left [x];
| | end else begin {t > val [x]}
| | | x := right [x];
| | end;
| end;
| if t <> val [x] then begin {t нет в дереве}
| | get_free (i);
| | left [i] := null; right [i] := null;
| | val [i] := t;
| | if t < val [x] then begin
| | | left [x] := i;
| | end else begin {t > val [x]}
| | | right [x] := i;
| | end;
| end;
end;