Обход дерева. Перебор с возвратами
3.1. Ферзи, не бьющие друг друга: обход дерева позиций
В предыдущей лекции мы рассматривали несколько задач одного
и того же типа: "перечислить все элементы некоторого
множества  ". Схема решения была такова: на
множестве
". Схема решения была такова: на
множестве  вводился порядок и описывалась процедура перехода от произвольного элемента множества
вводился порядок и описывалась процедура перехода от произвольного элемента множества  к следующему за ним (в этом порядке). Такую схему не всегда удается реализовать непосредственно, и в этой лекции мы
рассмотрим другой полезный прием перечисления всех
элементов некоторого множества. Его называют " поиск
с возвратами ", " метод ветвей и границ ", " backtracking ". На наш взгляд, наиболее точное название этого метода - обход дерева.
к следующему за ним (в этом порядке). Такую схему не всегда удается реализовать непосредственно, и в этой лекции мы
рассмотрим другой полезный прием перечисления всех
элементов некоторого множества. Его называют " поиск
с возвратами ", " метод ветвей и границ ", " backtracking ". На наш взгляд, наиболее точное название этого метода - обход дерева.
3.1.1.Перечислить все способы расстановки  ферзей на шахматной
доске
ферзей на шахматной
доске  , при которых они не бьют друг друга.
, при которых они не бьют друг друга.
Решение. Очевидно, на каждой из  горизонталей должно
стоять по ферзю. Будем называть k-позицией (для
горизонталей должно
стоять по ферзю. Будем называть k-позицией (для 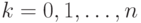 ) произвольную расстановку
) произвольную расстановку  ферзей на
ферзей на  нижних горизонталях (ферзи могут бить друг друга).
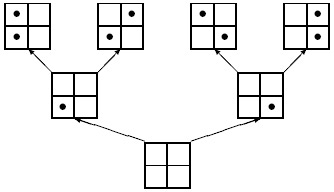
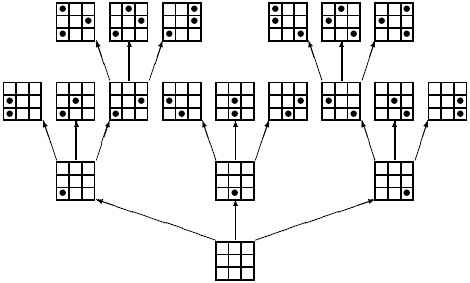
Нарисуем "дерево позиций": его корнем будет
единственная
нижних горизонталях (ферзи могут бить друг друга).
Нарисуем "дерево позиций": его корнем будет
единственная  -позиция, а из каждой
-позиция, а из каждой  -позиции выходит
-позиции выходит  стрелок вверх в
стрелок вверх в 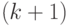 -позиции. Эти
-позиции. Эти  позиций отличаются положением ферзя на
позиций отличаются положением ферзя на 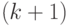 -ой горизонтали. Будем считать, что расположение их на рисунке соответствует положению этого ферзя: левее та позиция, в которой ферзь расположен левее.
-ой горизонтали. Будем считать, что расположение их на рисунке соответствует положению этого ферзя: левее та позиция, в которой ферзь расположен левее.
Среди позиций этого дерева нам надо отобрать те  -позиции, в которых ферзи не бьют друг друга.
Программа будет "обходить дерево" и искать их.
Чтобы не делать лишней работы, заметим вот что: если
в какой-то
-позиции, в которых ферзи не бьют друг друга.
Программа будет "обходить дерево" и искать их.
Чтобы не делать лишней работы, заметим вот что: если
в какой-то  -позиции ферзи бьют друг друга, то
ставить дальнейших ферзей смысла нет. Поэтому, обнаружив
это, мы будем прекращать построение дерева в этом
направлении.
-позиции ферзи бьют друг друга, то
ставить дальнейших ферзей смысла нет. Поэтому, обнаружив
это, мы будем прекращать построение дерева в этом
направлении.
Точнее, назовем  -позицию допустимой, если
после удаления верхнего ферзя оставшиеся не бьют
друг друга. Наша программа будет рассматривать только
допустимые позиции.
-позицию допустимой, если
после удаления верхнего ферзя оставшиеся не бьют
друг друга. Наша программа будет рассматривать только
допустимые позиции.