Обход дерева. Перебор с возвратами
3.1.7.Доказать, что число операций в этой программе по порядку равно числу вершин дерева. (Как и в других программах, которые отличаются от этой лишь пропуском некоторых команд обработать.)
Указание. Примерно каждое второе действие при исполнении этой программы - обработка вершины, а каждая вершина обрабатывается максимум дважды.
Вернемся теперь к нашей задаче о ферзях (где из всех
программ обработки дерева понадобится лишь первая,
самая простая).
Реализуем операции с деревом позиций. Позицию будем
представлять с помощью переменной k: 0..n (число ферзей)
и массива c: array[1..n] of 1..n ( c[i] -
координаты ферзя на i -ой горизонтали; при  значение c[i] роли не играет).
Предполагается, что все позиции допустимы (если убрать
верхнего ферзя, остальные не бьют друг друга).
значение c[i] роли не играет).
Предполагается, что все позиции допустимы (если убрать
верхнего ферзя, остальные не бьют друг друга).
program queens;
| const n = ...;
| var
| k: 0..n;
| c: array [1..n] of 1..n;
|
| procedure begin_work; {начать работу}
| begin
| | k := 0;
| end;
|
| function danger: boolean; {верхний ферзь под боем}
| | var b: boolean; i: integer;
| begin
| | if k <= 1 then begin
| | | danger := false;
| | end else begin
| | | b := false;
| | | i := 1;
| | | {b <=> верхний ферзь под боем ферзей с номерами < i}
| | | while i <> k do begin
| | | | b := b or (c[i]=c[k]) {вертикаль}
| | | | or (abs(c[i]-c[k]))=abs(i-k)); {диагональ}
| | | | i := i+1;
| | | end;
| | | danger := b;
| | end;
| end;
|
| function is_up: boolean; {есть_сверху}
| begin
| | is_up := (k < n) and not danger;
| end;
|
| function is_right: boolean; {есть_справа}
| begin
| | is_right := (k > 0) and (c[k] < n);
| end;
| {возможна ошибка: при k=0 не определено c[k]}
|
| function is_down: boolean; {есть_снизу}
| begin
| | is_down := (k > 0);
| end;
|
| procedure up; {вверх_налево}
| begin {k < n, not danger}
| | k := k + 1;
| | c [k] := 1;
| end;
|
| procedure right; {вправо}
| begin {k > 0, c[k] < n}
| | c [k] := c [k] + 1;
| end;
|
|
| procedure down; {вниз}
| begin {k > 0}
| | k := k - 1;
| end;
|
| procedure work; {обработать}
| | var i: integer;
| begin
| | if (k = n) and not danger then begin
| | | for i := 1 to n do begin
| | | | write ('<', i, ',' , c[i], '> ');
| | | end;
| | | writeln;
| | end;
| end;
|
|
| procedure UW; {вверх_до_упора_и_обработать}
| begin
| | while is_up do begin
| | | up;
| | end
| | work;
| end;
|
begin
| begin_work;
| UW;
| while is_down do begin
| | if is_right then begin
| | | right;
| | | UW;
| | end else begin
| | | down;
| | end;
| end;
end.3.1.8.Приведенная программа тратит довольно много времени на выполнение проверки есть_сверху (проверка, находится ли верхний ферзь под боем, требует числа действий порядка n ). Изменить реализацию операций с деревом позиций так, чтобы все три проверки есть_сверху/справа/снизу и соответствующие команды требовали бы количества действий, ограниченного не зависящей от n константой.
Решение. Для каждой вертикали, каждой восходящей и каждой нисходящей диагонали будем хранить булевское значение - сведения о том, находится ли на этой линии ферзь (верхний ферзь не учитывается). (Заметим, что в силу допустимости позиции на каждой из линий может быть не более одного ферзя.)
3.2. Обход дерева в других задачах
3.2.1.Использовать метод обхода дерева для решения следующей задачи: дан массив из n целых положительных чисел ![{a[1]}\ldots{a[n]}](/sites/default/files/tex_cache/dce62e79eefc8a3d30d7b9890da6b90f.png) и число s ; требуется узнать,
может ли число s быть представлено как сумма некоторых
из чисел массива a. (Каждое число можно использовать не
более чем по одному разу.)
и число s ; требуется узнать,
может ли число s быть представлено как сумма некоторых
из чисел массива a. (Каждое число можно использовать не
более чем по одному разу.)
Решение. Будем задавать k -позицию
последовательностью из k булевских значений,
определяющих, входят ли в сумму числа ![{a[1]}\ldots{a[k]}](/sites/default/files/tex_cache/e3ade0a5a30142eda838acbb46ad7706.png) или не входят. Позиция допустима, если ее сумма не превосходит s.
или не входят. Позиция допустима, если ее сумма не превосходит s.
Замечание. По сравнению с полным перебором всех  подмножеств тут есть некоторый выигрыш. Можно
также предварительно отсортировать массив a в убывающем
порядке, а также считать недопустимыми те позиции,
в которых сумма отброшенных членов больше, чем разность
суммы всех членов и s. Последний прием называют "методом ветвей и границ". Но принципиального улучшения по
сравнению с полным перебором тут не получается (эта задача,
как говорят,
подмножеств тут есть некоторый выигрыш. Можно
также предварительно отсортировать массив a в убывающем
порядке, а также считать недопустимыми те позиции,
в которых сумма отброшенных членов больше, чем разность
суммы всех членов и s. Последний прием называют "методом ветвей и границ". Но принципиального улучшения по
сравнению с полным перебором тут не получается (эта задача,
как говорят, 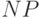 -полна, подробности см. в книге Ахо,
Хопкрофта и Ульмана "Построение и анализ вычислительных алгоритмов", Мир, 1979, а также в книге Гэри и Джонсона "Вычислительные машины и труднорешаемые задачи", Мир,
1982). Традиционное название этой задачи - "задача
о рюкзаке" (рюкзак общей грузоподъемностью s нужно
упаковать под завязку, располагая предметами веса
-полна, подробности см. в книге Ахо,
Хопкрофта и Ульмана "Построение и анализ вычислительных алгоритмов", Мир, 1979, а также в книге Гэри и Джонсона "Вычислительные машины и труднорешаемые задачи", Мир,
1982). Традиционное название этой задачи - "задача
о рюкзаке" (рюкзак общей грузоподъемностью s нужно
упаковать под завязку, располагая предметами веса ![{a[1]}\ldots{a[n]}](/sites/default/files/tex_cache/dce62e79eefc8a3d30d7b9890da6b90f.png) ). См. также в
"Как обойтись без рекурсии"
(Как обойтись без рекурсии) алгоритм ее решения, полиномиальный по
). См. также в
"Как обойтись без рекурсии"
(Как обойтись без рекурсии) алгоритм ее решения, полиномиальный по  (использующий "динамическое программирование").
(использующий "динамическое программирование").
3.2.2.
Перечислить все последовательности из  нулей, единиц и двоек, в которых никакая группа цифр не повторяется два раза подряд (нет куска вида
нулей, единиц и двоек, в которых никакая группа цифр не повторяется два раза подряд (нет куска вида  ).
).
3.2.3.
Аналогичная задача для последовательностей нулей и единиц,
в которых никакая группа цифр не повторяется три раза
подряд (нет куска вида  ).
).
К этой же категории относятся задачи типа "можно ли сложить данную фигуру из пентамино" и им подобные. В них важно умелое сокращение перебора (вовремя распознать, что имеющееся расположение фигурок уже противоречит требованиям, и по этой ветви поиск не продолжать).
